Catching primes

June 2008

Prime numbers play a hugely important role as the fundamental building blocks of our number system — and they remain at the centre of some of the biggest mysteries of mathematics. Prime numbers are those whole numbers that can only be divided by themselves and the number 1. For example, 7 is a prime, but 6 is not, because 6 = 2 × 3. Non-primes are known as composite numbers

What makes primes the fundamental building blocks of our number system is the fact that every whole number can be written as a product of prime numbers. For example, the number 60 can be written as 60 = 2 × 2 × 3 × 5. What's more, there's only one way of doing this. Any expression for 60 as a product of primes involves precisely the same primes, but possibly arranged in a different order.

Because of their important role in number theory, mathematicians make sustained efforts to discover the properties of the sequence of primes as a whole, and to identify further primes. We have known for over 2000 years that there are infinitely many primes, but there is no single formula which produces all prime numbers. However, there are procedures that systematically generate a list of all the primes up to a given size. Here, we'll look at a method that does this visually, so that the sequence of primes unfolds before our eyes.

The method is called the visual sieve because it sieves out the composite numbers, leaving the primes behind. It was devised by Yuri Matiyasevich and Boris Stechkin, mathematicians working within the Steklov Mathematical Institute of the Russian Academy of Sciences. At the heart of the method lies this diagram:

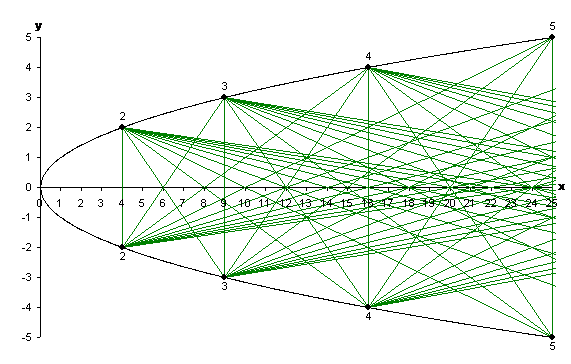
Figure 1: The visual sieve.

If you look closely, you might be able to see how this diagram relates to the primes. You might also notice that the diagram actually looks rather like a sieve — a nice convergence between the mathematical language and the object it describes! For now, though, we'll construct this diagram step by step. We'll discover how, as we follow the steps, the sequence of primes emerges.

Making a sieve

We begin with a basic background diagram. We draw $x$ and $y$ -axes and mark the positive $x$ -axis with $1,2,3,\cdots$ and the $y$ -axis with $\cdots ,-2,-1,0,1,2,\cdots$ . These axes are shown below.

Figure 2: The axes.

On these axes we plot the curve $x = y^2$ . To clarify, at every point $(x,y)$ on this curve, we have $x = y^2$ . For example, two points lying on the curve are $(4,2)$ and $(9,-3)$ . This type of curve is known as a parabola.

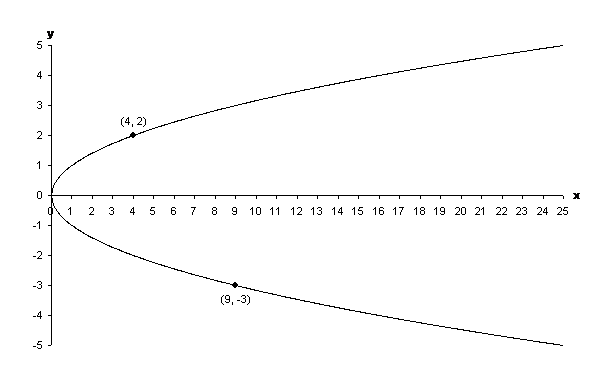
Figure 3: The parabola.

To complete the basic diagram, we will mark two sets of points lying on the parabola. To form the first set, we begin by marking the point $(4,2)$ and labelling it with $2$ , and then marking the point $(9,3)$ and labelling it with $3$ . We continue, marking the point $(i^2,i)$ for every whole number $i$ greater than or equal to $2$ . We will need to choose a suitable point to stop; this will depend on the size of our sheet of paper (or computing capacity)! We label each point $(i^2,i)$ with $i$ . These points all lie on the upper half of the parabola. We form the second set of points by marking the point $(j^2,-j)$ for every whole number $j$ greater than or equal to $2$ , and labelling it with $j$ . These points all lie on the lower half of the parabola.

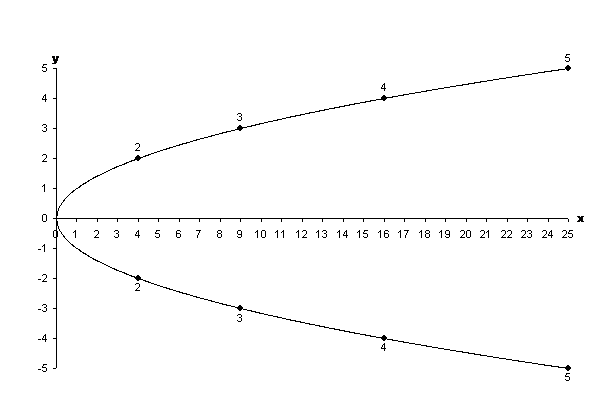
Figure 4: Marking points.

The visual sieve diagram at the beginning contains a great many straight lines. We're now going to add these straight lines to our basic diagram in groups. We'll add each line by joining a pair of points marked on the parabola - always joining a point on the upper half with one on the lower half. We'll start by joining the points $(4, 2)$ and $(4,-2)$ , as shown below.

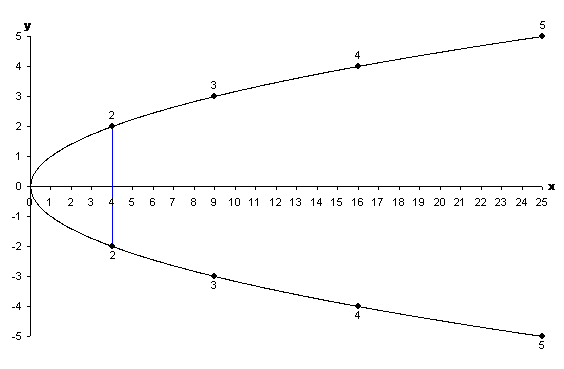
Figure 5: The first line.

We then join the pairs $(4,2)$ and $(9,-3)$ ; and $(4,2)$ and $(16,-4)$ . We continue, joining $(4,2)$ to every point we've marked on the lower half of the parabola. The result is shown below.

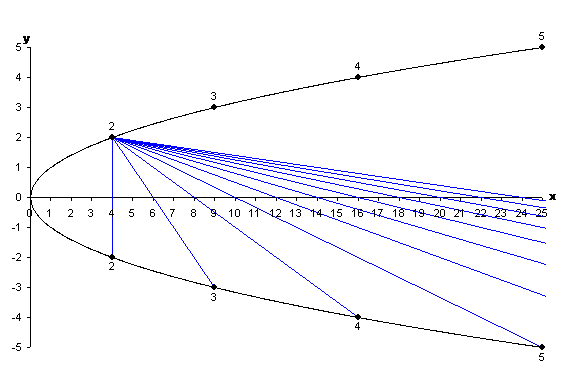
Figure 6: The first group of lines.

Next we do all this the other way up, joining $(4,-2)$ to every point marked on the upper half of the parabola. We've now drawn in the two first groups of lines, and together they're shown below.

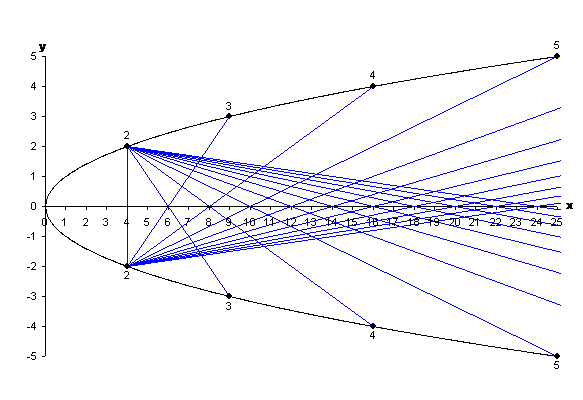
Figure 7: The first two groups of lines.

We now repeat this process, taking each of the points marked on the upper section, i.e. $(9,3)$ , $(16,4)$ , $(25,5)$ , $(36,6)$ and so on, and each point marked on the lower section, as our starting points. We've now completed the diagram, and the whole thing is pictured again below.

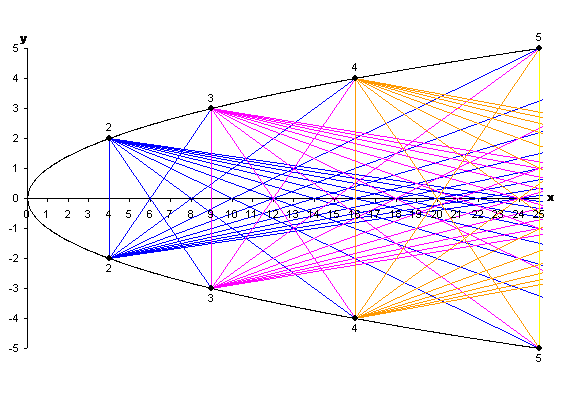
Figure 8: The complete visual sieve.

Let's pause for a moment to consider what we've actually done here. For each pair of whole numbers $i$ and $j$ , greater than or equal to $2$ , we've joined the points $(i^2,i)$ and $(j^2,-j)$ . Let's give the line we've drawn a name - say $L(i,j)$ . Now we're able to single out any line we like for our attention; for example, on the diagram below the line $L(3,4)$ is marked in red.

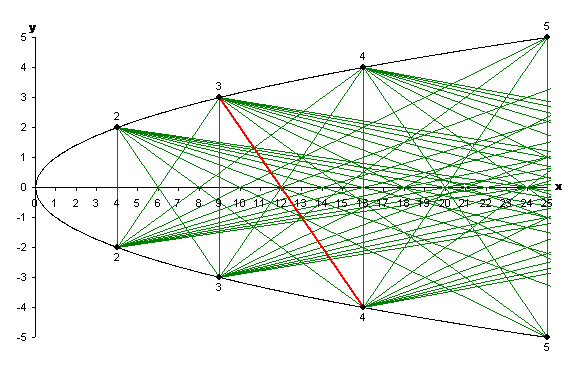
Figure 9: The line L(3,4) marked in red.

What's happening?

Let's now look at what the visual sieve is telling us. For the moment we'll focus our attention on the $x$ -axis. As we run our eye along it, from left to right, we'll pass over the markings for all the positive whole numbers. We can see that some of these whole number points are crossed out by a line (or several lines) passing through them - while others are not. At this point we might well wonder whether there's any significance in this. Well, it turns out that all the composite numbers are crossed out by lines, while all the prime numbers are not! The sequence of primes simply emerges before our eyes as we build up the diagram.

Why does it work?

So why are the composites crossed out while the primes aren't? It's all because of one fundamental fact about the lines we've drawn on our diagram. Before we explore this fact let's recall our way of describing the lines we added. If $i$ and $j$ are any two whole numbers greater than or equal to $2$ , then $L(i,j)$ is the line joining the points $(i^2,i)$ and $(j^2,-j)$ . Now, instead of thinking about which points on the $x$ -axis are crossed out, and which aren't, we can turn the question around, and ask which point is crossed out by each line $L(i,j)$ . It turns out that the line $L(i,j)$ actually crosses out the point $i \times j$ ! For example, the line $L(2,3)$ joining $(4,2)$ and $(9,-3)$ crosses out the number $2 \times 3 = 6$ . This fact explains everything: any composite number $n$ can be factorised into $n = i \times j$ , where each of $i$ and $j$ is at least $2$ . There may be more than one way of doing this, but we just need to choose one. Of course, the numbers $i$ and $j$ in this factorisation depend completely on the number $n$ we started with. If we then turn to the line $L(i,j)$ , we know that it crosses out the number $i \times j$ . But this is equal to $n$ itself, so we know that $n$ is crossed out! On the other hand, what happens to a prime number $p$ ? Well, we know that there's no way of factorising $p$ into $i \times j$ with both $i$ and $j$ at least $2$ . So that means that there's no line $L(i,j)$ which crosses out $p$ .

But why does $L(i,j)$ cross out $i \times j$ ? This is really the same as asking: why does the line $L(i,j)$ meet the $x$ -axis at the point $(i \times j,0)$ ? We can answer this using geometry. We'll pretend for now that we know nothing about where the line meets the $x$ -axis, and we'll use some geometrical ideas to find the meeting point from scratch.

Very different things will happen depending upon whether $i$ and $j$ are equal or unequal. Let's look first at what happens if they're equal. The line $L(i,j)$ now looks as shown in the diagram below. The scales and labels have been omitted so that we are representing any $L(i,i)$ rather than a specific one.

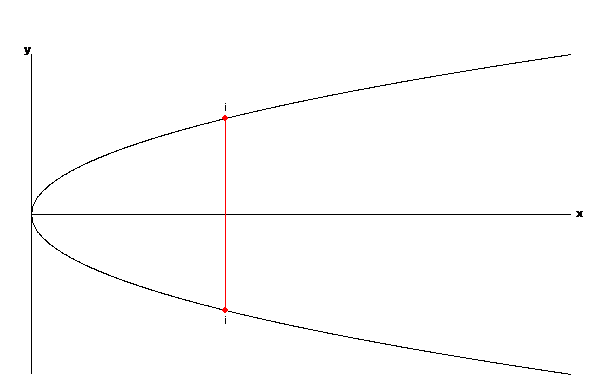
Figure 10: The line L(i,i).

We see that $L(i,j)$ is a vertical line, and that any point lying on it has the same $x$ -coordinate, $i^2$ (or $j^2$ , since that's the same). So the point where $L(i,j)$ meets the $x$ -axis also has $x$ -coordinate $i^2$ . But this is equal to $i \times j$ , because $i$ and $j$ are equal. This is the result we expected, and that's dealt with what happens if $i$ is equal to $j$ .

From now on we can work on the assumption that the whole numbers $i$ and $j$ are not equal. We can draw the line $L(i,j)$ , and note some important features. The figure below shows the situation when $j$ is greater than $i$ ; we will concentrate on this, because the situation when $j$ is less than $i$ is very similar.

Figure 11: The line L(i,j).

Here we mark the two points $(i^2,i)$ and $(j^2,-j)$ , and the point where the line $L(i,j)$ meets the $x$ -axis, which we'll call $P$ . We want to find the $x$ -coordinate of this point $P$ , so let's give it the name $s$ . The next thing we'll do is to form two triangles using the points we've marked.

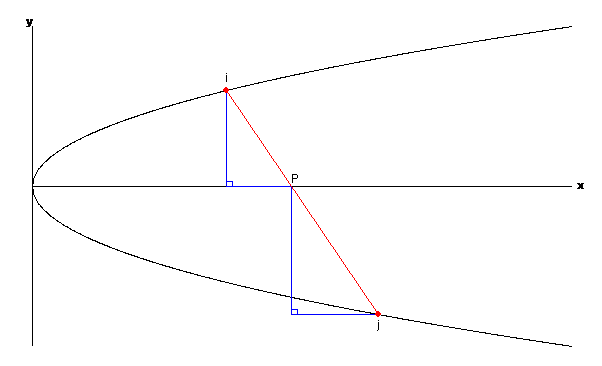
Figure 12: Forming two triangles.

The first triangle has corners at $(i^2,i)$ (this is the point on the upper half of the parabola) $(i^2,0)$ (the point directly below on the x-axis) and $P$ . One of its sides is a segment of the line $L(i,j)$ , and it has a right angle at $(i^2,0)$ . The second triangle has corners at $P$ , $(j^2,-j)$ (the point on the lower half of the parabola) and $(s,-j)$ , (the point directly below $P$ ). Again, a segment of the line $L(i,j)$ forms one of its sides, and the angle opposite that side is a right angle. We can now mark on the diagram the lengths of some of the sides of these triangles. The first triangle has vertical side of length $i$ and horizontal side of length $s - i^2$ . The second has vertical side of length $j$ and horizontal side of length $j^2 - s$ .

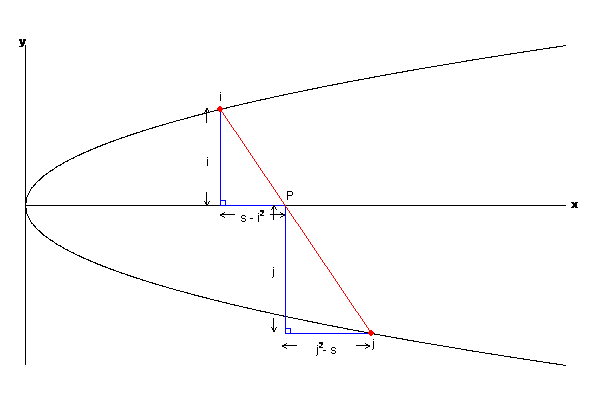
Figure 13: Side lengths.

We're now in a position to exploit the fact that these two triangles are similar: one is a scaled-up version of the other. Another way of saying this is that the ratios between corresponding pairs of sides of the two triangles are the same. This translates into symbols as

$\frac{i}{s - i^2} = \frac{j}{j^2 - s}.$

So now we have an equation relating $i$ , $j$ , and $s$ . We just have to see whether we can rearrange it and obtain $s$ expressed in terms of $i$ and $j$ . Starting with

$\frac{i}{s - i^2} = \frac{j}{j^2 - s}$

we'll multiply both sides of the equation by both $s - i^2$ and $j^2 - s$ . Then we'll collect everything involving $s$ on the left-hand side, and everything else on the right. Here are the steps we go through:

$\frac{i}{s - i^2}\, = \frac{j}{j^2 - s}$

$i (j^2 - s) = j (s - i^2)$

$ij^2 - is \, = js - ji^2$

$\; \; -is - js \; \; \; = \; \; -ji^2 - ij^2$

$-(i+j)s \; = \; -ij (i+j)$

$\; \; \; \; s \; \; \; \, \; = \; \; \; ij$

So we've found that $s = i \times j$ . This means that, on the visual sieve diagram, the line $L(i,j)$ meets the $x$ -axis at the point with $x$ -coordinate $i \times j$ . That's exactly what we were trying to find out! This tells us that the line $L(i,j)$ does cross out the number $i \times j$ . So we've seen that each line $L(i,j)$ crosses out the number $i \times j$ . This in turn completes the explanation of why any composite number is crossed out by one of our lines $-$ while no prime number is. So, as we build up the sieve diagram step by step, all the composite numbers are crossed out one by one, and the primes gradually appear in the gaps between them. I find the way this happens highly appealing $-$ I hope you do too!

About the author

Abi grew up in the north of England, and moved south to study maths at Imperial College, London, and Queen Mary, University of London. She now teaches maths at the Open University and is working on a research project on on-line tutorials. Abi's main mathematical interest is group theory.

Comments

An alternative graphical method

Superimpose the graphs of y = sin(πx/n) for n = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... on a single pair of axes.
These curves intersect the x-axis when x = kn
and intersections which belong to only one curve correspond to prime values of n.