Strange attractors

It has long been known that small systems of interacting agents can produce regular behaviour. For example, in a population of foxes and hares, the rates of change of the number of each can be written as an interdependent system of differential equations. As the hare population grows, there is more food for the foxes so they enjoy a population explosion. But then the hares die out, the foxes starve, and the cycle repeats. A graph of hares versus foxes (the "phase-space" of the system) shows a smooth loop - a limit cycle.

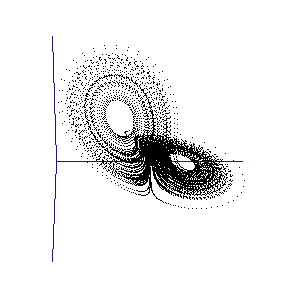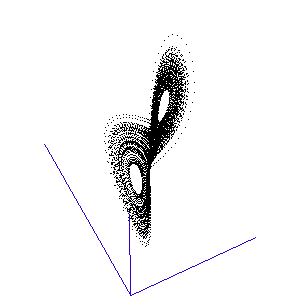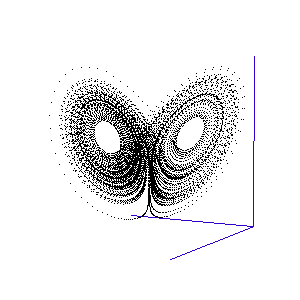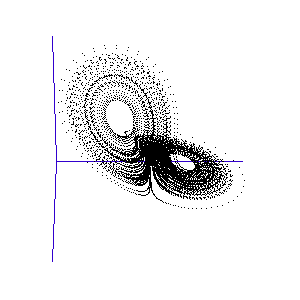
Figure 1: A system with 3 linked variables exhibiting chaos - the Lorenz Attractor

However, more complex systems, with three or more differential equations coupled together, often cannot be solved analytically but must instead be modelled step by step on a computer. One of the first such mathematical systems was developed by Edward Lorenz, who was attempting to model the weather with three coupled equations. The solution at each time-step can be plotted on a three-dimensional graph, as shown in the animation in Figure 1.

Lorenz discovered that even though the system was very simple, and completely deterministic (the trajectory can be calculated precisely from the equations), it produced an unpredictable and seemingly random output - chaos. This system has become known as the Lorenz strange attractor, and many more such systems are now known. In fact, it seems that interacting systems, especially those with more than three coupled variables, often exhibit chaotic behaviour. Ordered or rhythmic behaviour does not appear to be the norm.

Neurones and chaos

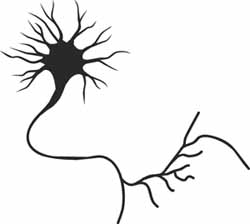
A neurone is a special electrically-active cell that can transmit pulses of voltage along its length. Each pulse looks like a "spike" on a trace of voltage over time. Pulses are produced as floods of ions rush back and forth through two groups of channels spanning the neurone's membrane: those with fast dynamics and those with slow. Of course, a real living neurone is a complicated thing, but it turns out that the flow of electricity across the membrane can be well modelled by a system of three interdependent differential equations. These describe the change over time in the speed at which the voltage across the membrane changes, and two other variables: fast channel current and slow channel current.

Such a simple model accurately reproduces the behaviour-types of a single nerve cell: silent, or firing regularly, or spiking chaotically, as the system moves between different regions of the phase-space. This perfectly demonstrates the elegance of a mathematical approach: the hopelessly complicated reality, with numerous different channels opening and closing independently, and ions flowing in and out through them, has been condensed down to its essence of just three linked equations. The model accurately predicts the behaviour of an isolated neurone observed in a lab as the experimenter forces the voltage up: first staying still, then spiking rhythmically, then with two pulses in every beat, then three, until finally the output degenerates into chaos, as seen in Figure 2.

Nerve cells are also capable of another type of firing behaviour, called "bursting". The voltage rises slowly until a particular threshold is passed and then the neurone suddenly fires off a rapid series of spikes before falling quiet again. The important detail is that the spikes become less and less regular towards the end of a burst, as if the neurone is steadily descending back into a chaotic regime before shutting off. This mode is more important when we consider networks of connected neurones, and can be seen in Figure 3.

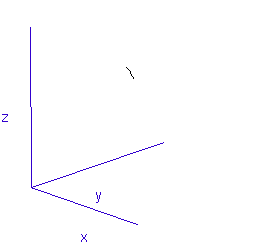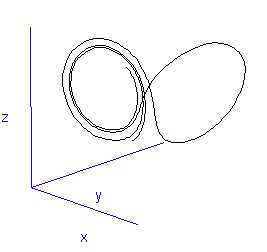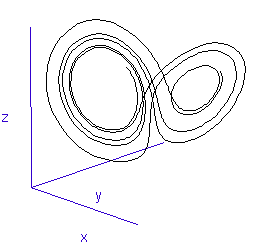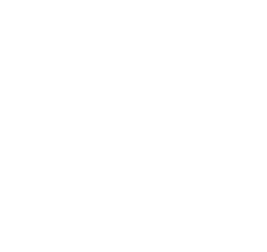
Figure 2: The trajectory of a fly trapped in the room of Lorenz phase-space.

For a three-variable system like this, the situation is much like a fly buzzing around inside a large square room. The axes (the width, length, and height of the room) represent the three interdependent parameters that affect the behaviour of the system. Different combinations create different behaviours in the system, and the fly has particular flight paths in separate zones of the room. Some parts of the system's phase-space, ie regions of air within the room, exhibit semi-periodic behaviour. The fly is spiralling gently downwards, or looping the loop near the ceiling, and its path is largely predictable. This corresponds to a neurone spiking regularly. At other times, it is as if the fly strays a touch too close to some invisible point in the middle of the room and as a result zooms off in highly variable directions. These are the chaotic regions of the phase space, and they can throw the fly between distant spots in the room, rapidly switching its flight behaviour - for example from spiralling to looping.

Such a switching region can be seen in the animation of the Lorenz attractor in Figure 3. Here the "fly" spends a short while looping around one of the lobes, before its path strays too close to the middle and it is shunted over to the other side.

Controlling the chaos

If two chaotic neurones are coupled together with an inhibitory link, so that while one is firing it prevents the other from doing so, then the two neurones can effectively modulate each other. They fall into ordered oscillations, out of phase with each other, and synchronised so that as one finishes bursting the other starts up. The two neurones alternate in activity, like the steady tick-tock of a clock.

More neurones can be added to form a small loop-like circuit, each mutually inhibiting its two neighbours. Now each of the neurones produces a perfect oscillating pattern (remember, the behaviour of each in isolation would be chaotic). Due to the inhibition, every neurone bursts in opposite phase to its neighbours - resulting in alternating neurones firing in a synchronised rhythm, like a group drumbeat. Thus, the interactions between the neurones have collectively regularised their own output.

In fact, it seems to be a general feature of both the models we build of neurones and the neurones themselves that their output is much more regular when they are assembled into linked networks, rather than acting individually - the coupling itself seems to suppress chaos.

There is a clue to the way neural circuits control the disruptive forces of chaos in the trace in Figure 3. After the inhibition has been lifted the neurone starts bursting, but, as described already, the spikes get progressively more and more irregular. However, just before it starts behaving completely chaotically, its neighbour begins inhibiting again and shuts it off. Each new burst begins afresh with a more or less regular rhythm of firing - the neurone has been reset. One of the reasons, therefore, that networks of neurones are more stable than any of the individual cells might be that through the inhibition they keep shifting each other back into phase-regions further away from the chaotic regime. It is almost as if the fly is caught in a whirlpool and is being swirled closer and closer to a chaotic regime in the centre. The electrical effect of neurone inhibition is like rescuing the fly before it finally spirals into the chaotic hole, moving it to a more stable region of the phase space, and then releasing it again at the start of the next burst.

Central Pattern Generators

It is exactly this kind of neural network, a staggeringly simple six-neurone loop, that produces patterned output driving the heartbeat of the leech. Such assemblies of nerve cells are called Central Pattern Generators, or CPGs. The out-of-phase rhythms cause two opposing sets of muscles to contract and pump blood around the body. A chemical signal called a neuromodulator can be released onto this circuit to reduce the degree of inhibitory coupling between the individual neurones, and the pace of the drumbeat increases.

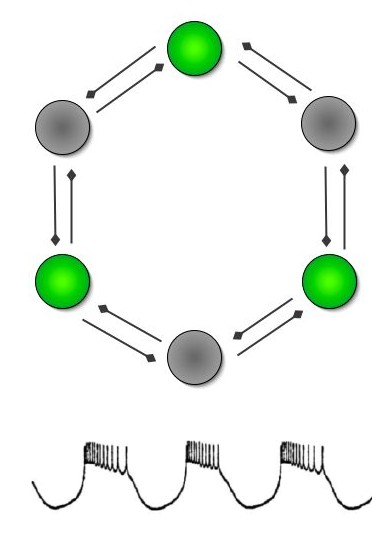
Figure 3: The mutually inhibited six-neurone circuit controlling the leech heart. Each half of the neural network produces the series of bursts shown at the bottom. Here neurones 1, 3, and 5 are firing while the others are silent. The spikes within each burst get increasingly erratic.

The much more complex behaviour of "higher" organisms is controlled by larger, more complicated neural networks. And in such complex multi-dimensional systems chaotic regimes may be unavoidable, so the firing output of neurones may be inherently chaotic, with this chaos actively suppressed by the wiring of neural circuits. Without the control of periodic inhibition the neurones would all quickly degenerate into erratic behaviour.

Some independent CPGs have been identified in such higher organisms, for example in amphibians like salamanders the same CPG controls both swimming in water and walking on land, and must be able to switch quickly between the two necessary patterns. The neural network that controls swallowing in cats is rapidly reconfigured to generate the muscle contractions required for coughing. Many of these assemblies are located in the spinal cord and operate independently of the main brain - explaining why headless chickens really are able to run around.

We see that animals need neural circuits that not only produce useful, regular patterns, but that can also shift quickly between different modes to meet changing requirements. This hints at a deeper influence of chaos in our brains: it is starting to look as if evolution has tuned neurones so that they usually operate right on the brink of the chaotic pits in phase-space. Could this just be due to the mathematics of such systems - large regions of the phase-space are rotten with chaotic regimes, especially in complex systems with many interacting components, with the result that any semi-stable trajectory is never far from falling into one? Or is chaos somehow vital to the proper working of our brains?

Neuroscientists are coming to believe the latter. Even though chaos is suppressed by networks, it is thought that the inherent instability of the individual neurones is vital to the working of CPGs and processing networks. It is not simply that neurones are able to cope with inevitable chaos: they have evolved to exploit it. Neurones need to be able to switch quickly between different states, and that is precisely what a chaotic trajectory does within the phase-space. A neurone in a dormant state waiting for the signal to spike, or one already in a smooth, regular pattern of firing (ie a semi-periodic cycle), is in a stable configuration and cannot quickly jump across phase-space to alter its firing pattern.

Modern fighter jets like this F22 are deliberately designed to be unstable to make them more manoeuvrable.

If neurones instead function right on the edge of chaos, as demonstrated by those with the bursting output, that very instability allows them to alter their behaviour rapidly as necessary. Chaotic systems, by definition, are sensitive to their initial conditions. So only the slightest nudge, or "perturbation" in maths-speak, is needed to knock a system following one particular trajectory onto a completely different one that quickly takes it to another region of the phase-space. The metaphorical butterfly need only flap its wings to create a tornado.

Neurones operating in inherently unstable regions of the phase-space thus need only the slightest input to settle quickly into a new pattern. It's as if the fly is hit by a minute puff of air that pushes it closer to a switch point in the room, and is thrown from gentle spirals near the ceiling to furious looping by the skirting board. A similar philosophy informs the design of modern fighter jets: planes such as the F22 are inherently aerodynamically unstable and can only be controlled with the aid of computers. The flip-side is that they are extremely quick to respond to commands, and so highly manoeuvrable in the air.

Proteus

Aside from being crucial for the effective functioning of CPGs and other processing networks in the brain, chaos may hold the key to understanding another type of animal behaviour that often makes the difference between life and death. When a predator pounces, simply escaping in the opposite direction is often the worst option. Your course is entirely predictable and can be anticipated by the predator. Much better to dodge randomly - a strategy that has been re-evolved many times by nature on land, sea and air, and even during research into artificial intelligence. For example, two robots, a slow but manoeuvrable "prey" and a faster but less agile "predator", are given simple neural networks with the capacity to evolve, and released in an arena together. The prey very soon learns that just running away from the predator as fast as it can is doomed to failure, whereas turning randomly to move in a zig-zag fashion is much more successful. Such an escape strategy of unpredictable movements is known as Protean evasion, after the Greek river god who eluded capture by continually changing form. The predators likewise evolve to be more cunning at anticipating the course of the prey in order to catch it.

Moth species able to hear the sonar calls from an echolocating bat often get some warning that the predator has locked on to them and is swooping in. In many cases they try an evasive flight pattern of tight turns, loops and powered dives, attempting to get themselves out of the narrow ultrasound beam so that the bat loses them. As a last-ditch effort they initiate very unpredictable movements, fluttering their wings irregularly so that they tumble around in the sky, making them a difficult target to catch. This erratic output is thought to come from the same CPG that normally produces the very regular rhythm for stable flight. Somehow the moth can trigger it to go chaotic instead, generating erratic wing-muscle twitches that help it dodge predators. The transition is extremely rapid and can be switched in just a few hundredths of a second - 10 times faster than the blink of an eye.

It is still largely unclear how the moth's CPG is wired up to enable it to flip-flop between these two behaviours, but the message is that sometimes an erratic output from a neural network is in fact extremely useful. Truly random behaviour is difficult to produce from neural networks (and people are notoriously bad at trying to imitate random processes), but a chaotic system, although not technically random, is a good approximation and can be unpredictable enough to confuse an approaching predator.

Unsurprisingly, if a CPG that is supposed to generate a regular pattern enters a chaotic regime of output then the consequences can be dire. The human heart, for example, is controlled by a population of pacemaker cells that ensure all the muscles fibres contract in a co-ordinated way and keep the heart pumping at a steady rate (which, like the leech heart, can be regulated by hormones such as adrenaline). If the output from these cells starts going awry the heart muscles no longer pull in unison but begin twitching chaotically, often leading to full-blown cardiac arrest. The solution is to deliver a sudden electric current across the heart to reset the firing pattern of the pacemakers, using the familiar shock paddles of a defibrillator. Other researchers think that the uncontrolled muscle spasms during an epileptic fit are due to neural networks in certain regions of the brain degenerating into a chaotic pattern.

Early research into systems of differential equations with more than three variables found that chaotic behaviour is all but inevitable for large swathes of the phase-space. Despite this, complex biological systems such as networks of nerve cells have evolved to tame chaos in order to produce the patterned output crucial for all animal behaviour. In fact, it is starting to seem that neurones have even gone a step further, and harnessed the powers of chaos to make neural circuits much more versatile and quick to adapt. Some insects even cultivate chaotic output to produce randomised behaviour. The hope is that by understanding how insects achieve this feat we will gather insights into controlling "dynamical diseases" such as epilepsy and heart fibrillation.

In Greek mythology, Chaos is the goddess of emptiness and confusion who gave birth to the Universe. Modern science is only just finding out that she may also give rise to human consciousness as well as disease.

About the author

Lewis Dartnell read Biological Sciences at Queen's College, Oxford. He is now on a four-year combined MRes-PhD program in Modelling Biological Complexity at University College London's Centre for multidisciplinary science, CoMPLEX. He completed the MRes last year, and is now just beginning a PhD in the field of astrobiology. He is using computer models of the magnetic fields on Mars to predict radiation levels, and whether alien life, or even future human explorers, could possibly be surviving near the surface.

In 2003 he came second in the THES/OUP science writing competition, and this year was awarded second prize in the Daily Telegraph/BASF Young Science Writer Awards. You can read more of Lewis's work at his homepage.