Masaki Kashiwara (PHOTO PABLO COSTA/ICM2018)

Masaki Kashiwara has won the 2018 Chern Medal at the International Congress of Mathematicians. This medal celebrates those who have made outstanding achievements in mathematics, and Kashiwara is recognised for his outstanding foundational contributions over the last 50 years: "Masaki Kashiwara's mark on current mathematics is exceptional."

One of the areas Kashiwara helped found is algebraic analysis. Building on the work of his professor in graduate school at the University of Tokyo, Mikio Sato, Kashiwara fully developed the concept of D-modules. These are mathematical structures that provide a fundamental bridge between the area of algebra and the area of analysis.

The building blocks of these structures are differential equations – something that is at the heart of all modern science and describe the relationship between things that vary. (For example, the speed of a moving object is captured by a differential equation describing the relationship between the change in distance travelled and the time the journey takes. You can read more about them, including an introduction, here.) But the framework used in D-modules is from a far more abstract part of mathematics, algebra, where the details are removed to focus on the heart of the abstract structures involved. D-modules have become a fundamental tool in many areas of mathematics. (If you'd like a technical introduction, you can read a beautiful translation of Kashiwara's Masters thesis.)

Kashiwara used D-modules to prove a long-standing and extremely important open problem in mathematics called the Riemann-Hilbert Problem, a generalisation of a famous problem posed by David Hilbert in 1900 (it was the 21st of 23 problems he posed).

You may remember from school that it's possible for an equation to have multiple solutions. For example, the equation $\sin(x) = 0$ has the solutions $0, \pi, 2\pi, ... k\pi$.

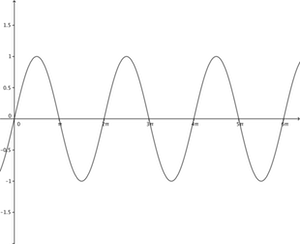
The function sin(x)

The function 1/x

This multi-valuedness is a particular problem if it occurs around something called a singularity, a point where an equation behaves strangely, rather than varying regularly as it does for the sine function. For example the function $1/x$ has a singularity at $x=0$ where it is undefined. For very small negative values of $x$ the function has a very large negative value, and for very small positive values of $x$ it has a very large positive value.

Mathematicians use something called a monodromy group of an equation to understand this strange behaviour. This group describes the topology – or shape – of a space that arises from the way the solutions to the equation change near the singularity.

Each of a type of differential equations called linear differential equations has an associated monodromy group. But the Riemann-Hilbert problem asks about the other direction: for every monodromy group, is there an associated linear differential equation whose behaviour near a singularity is described by that group? The case for equations involving one variable had been solved in the 1960s. In 1980s Kashiwara showed how to find the associated linear differential equation for any monodromy group. As well as an outstanding result in itself, the methods he used built an important bridge between algebraic analysis and topology.

Another area of mathematics that has benefited greatly from Kashiwara's contributions is representation theory. This is a way of describing abstract algebraic structures as something that is far better understood: as matrices operating on a vector space. (You can find out more about matrices and vectors here.)

An example of a crystal basis. Crystal bases have been used to prove formulas for the statistical behaviour of systems of particles. (Graphed using CrystalView. Image: Anne Schilling and Philip Starhill)

Kashiwara introduced the idea of crystal bases, which allow questions in representation theory to be answered in terms of combinatorics – or counting arguments. In particular it reveals the core of complex mathematical structures (represented as matrices acting over vector spaces) to be graphs. The vertices of these crystal graphs are the base – the "atomic elements" – of the mathematical structure, and the edges show how these atomic elements interrelate.

This work has had impacts across, and outside of, mathematics. Crystal bases have been particularly useful in mathematical physics where they are used to prove formulas for the statistical behaviour of systems of particles. Anne Schilling, Professor of Mathematics at the University of California, Davis, said: "Beyond its applications in representation theory and statistical mechanics, crystal bases have also had an impact on number theory, in particular automorphic forms and Dirichlet series. In fact, a whole semester program at the mathematical institute ICERM in 2013 was focused on this interplay between combinatorial representation theory (i.e. crystal bases) and number theory."

Kashiwara's work, with many different collaborators, continues to be ground-breaking. He proved an extension to his Riemann-Hilbert correspondence in 2016. His work has also inspired many mathematicians, and he has written text books that have become the "bibles" of their areas. His citation says: "Kashiwara's work stands out in depth, breadth, technical brilliance and extraordinary originality. It is impossible to imagine either algebraic analysis or representation theory without his contributions."

This content was produced in a collaboration with the London Mathematical Society.