Codes, computers and trees
Introduction
These days we take fast, reliable global telecommunications for granted. From our own homes we can ring up our friends all over the country, send facsimile reproductions of our documents to businesses overseas, and download files and web pages from all over the world.
It's easy to forget that it was less than 200 years ago that the first electronic communication system, the telegraph, was invented.
These days, most telecommunications are sent automatically from one telephone exchange or computer to another. In the old days of the telegraph, however, a human operator was required at each end. The sender would tap out messages in Morse code, which would be transmitted down the telegraph wire to a human decoder translating them back into ordinary characters.
Whereas written language uses alphabetic, numeric and punctuation characters, Morse code uses only two symbols: "dot", a short signal, and "dash", a long signal (by convention three times the length of dot). Different combinations of dots and dashes represent the different characters in an ordinary written message.
Today, there are many different ways of encoding written messages. We understand much better than did Samuel Morse the formal requirements of a good code. In this article, we'll be examining one important property of codes used to transmit messages from one place to another: the prefix property.
What is a code?
A code, for our purposes, is simply an organised way of representing information using a fixed, possibly small set of symbols. For example, modern computers rely on a binary (or two-element) code consisting only of the symbols 0 and 1. All the information on your computer (text, images, computer programs etc) is stored in a coded form as a sequence of 0s and 1s.
In order to solve the problem of storing alphabetic, numeric and other special characters on a computer, a code known as ASCII (American Standard Code for Information Interchange) was designed. Standard ASCII includes 128 different characters, and Extended ASCII adds an extra 128 to these.
In Standard ASCII, the various characters (including digits) are each given a unique number between 0 and 127. The character "A", for example, is number 65, and the character "a" is number 97.
However, our computers can only physically store 0s and 1s, and therefore these character numbers cannot be stored using our decimal numbering system: instead, they are stored as binary numbers using only 0s and 1s. Therefore Standard ASCII consists of 128 different code words based on a code alphabet consisting of the elements 0 and 1.
Table 1 shows the number, binary code word and actual character for ASCII characters numbers 32 to 127 (characters 0-31 are special "non-printable" characters, not shown here).
|
|
|
Based on the information in table 1.1, you can see that the alphabetic text
HELLO!would be stored on a computer in an ASCII code string as
100100010001011001100100110010011110100011
You may have noticed that some of the ASCII binary codes seem to be longer than they need to be. For example, the character "=" is represented by the binary code word "0111101". Why do we need the leading zero? Surely "111101" means the same thing? After all, both "09" and "9" mean nine.
As you can see from table 1, all the ASCII code words are the same length (7 binary digits for Standard ASCII and 8 binary digits for Extended ASCII). Now, the words in a code don't have to be all the same length, as we shall see. However, by making each code word contain a fixed number of binary digits we ensure that an important property called the prefix property holds true for the ASCII code.
Codes and the Prefix Property
Any code used for transmitting information must possess what is called the prefix property.
If a code has the prefix property, it means that no word in the code is a prefix of any other word in the code: in other words, that no longer code words begin with the identical digits making up any of the shorter code words.
As an example, let's consider a code made of code words of varying length. If 0 is a valid code word, then no other code word can start with 0 if we wish to preserve the prefix property. If 10 is a valid code word, then no other code word can start with 10.
Therefore, a valid five-word "prefix code" containing these two code words might look like one of these codes:
| Event | A | B | C | D | E |
| Code 1 | 0 | 10 | 110 | 1110 | 1111 |
| Code 2 | 1 | 00 | 011 | 0100 | 0101 |
The following codes, on the other hand, would be invalid because the prefix property does not hold:
| Event | A | B | C | D | E |
| Code 3 | 1 | 00 | 01 | 001 | 011 |
| Code 4 | 0 | 10 | 01 | 011 | 100 |
(In code 3, the code for B is a prefix of the code for D; the code for C is a prefix of the code for E. In code 4, the code for A is a prefix of the codes for C and D; the code for C is a prefix of the code for D).
The Prefix Property and Trees
An intuitive way of discovering whether or not the prefix property holds is by drawing a code tree.
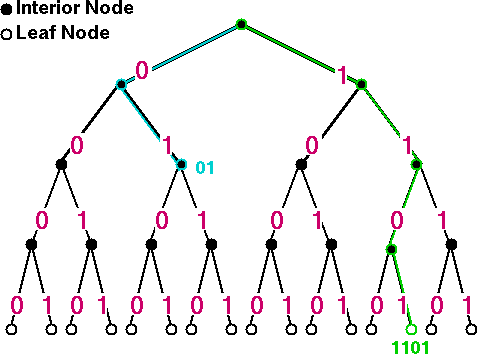
Figure 1: A binary code tree, showing code words 01 and 1101.
Figure 1 shows a binary code tree with four levels. We can build code words by starting at the top of the (upside-down) tree with an empty code word string "", and descending through the tree. At each branching point, we choose to go either left (digit 0) or right (digit 1) and we add this new digit to the end of our code word string.
For example, the blue path in figure 1 shows how we assemble code-word "01" (choosing first the left branch at level 1 - digit 0 - and then the right branch at level 2 - digit 1). The green path shows how we assemble code word "1101".
Note that nodes inside the tree, with other nodes hanging from them, are called interior nodes. Nodes at the bottom of the tree, with no such descendants, are called leaf nodes. In other words, code word 01 is located at an interior node in the tree of figure 1, and code word 1101 is located at a leaf node in this tree.
Now, this particular tree can be used to generate thirty different code words: two one-digit words at the first level (0 and 1), four two-digit words at the second level (00, 01, 10, 11), eight three-digit words at the third level, and sixteen four-digit words at the fourth level. Different kinds of trees (with more levels, fewer levels, missing branches etc) can generate different sets of code words.We already know that in a prefix code, no code word can be a prefix of any other code word. We would therefore expect that if we draw a code tree for a prefix code, all code words will be located at leaf nodes in that tree.
To draw a code tree for a particular code, we include all the nodes and branches required to form all the words in the codes, but no other nodes or branches. Accordingly, each of the four codes in tables 1.2 and 1.3 can represented using a code tree, as follows:
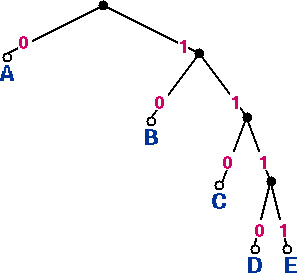
Figure 2 (left): Code tree for code 1, table 2.
In the code tree for code 1, a prefix code, each of the five code words is located at a leaf node; as expected, none of the interior nodes is a code word node.
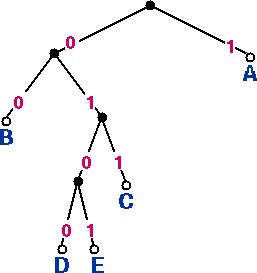
Figure 3 (right): Code tree for code 2, table 2.
Similarly, in the code tree for code 2, also a prefix code, each of the five code words is located at a leaf node.
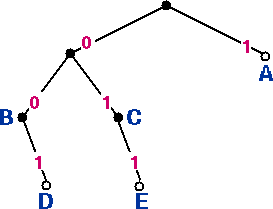
Figure 4 (left): Code tree for code 3, table 3.
Code 3 is not a prefix code: although code words A, D and E are located at leaf nodes in the code tree, nodes B and C are located at interior nodes.
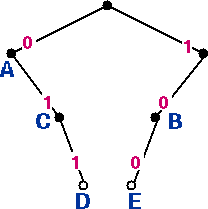
Figure 5 (right): Code tree for code 4, table 3.
Code 4 is also not a prefix code. Although code words D and E are located at leaf nodes, code words A, B and C are located at interior nodes.
As you can see, the prefix codes have their code words located entirely at leaf-nodes in the tree, whereas the non-prefix codes have code words located at interior nodes; these "offending" code words are prefixes of other words in the code.
Why do we need the prefix property?
Why is the prefix property important? Consider trying to send a message describing the following sequence of events:
A C D E B A C E
Using code 1 above (a valid code), the message looks like this.
0 1 1 0 1 1 1 0 1 1 1 1 1 0 0 1 1 0 1 1 1 1
There is only one way of breaking up the message into valid code words from left to right (or parsing it) - the intended way:
No code word is a prefix of any other code word, so the message is unambiguous, and is decoded into the correct original message A C D E B A C E.
Using code 4 above (an invalid code), the message looks like this:
0 0 1 0 1 1 1 0 0 1 0 0 0 1 1 0 0
However, there are multiple ways of parsing this message into valid code words:
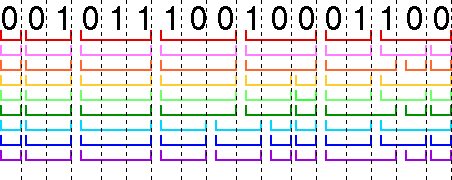
Because the code does not have the prefix property, the coded message is ambiguous. It can be decoded into all these different possible original messages:
| Parsing | Decoded message |
| Red | A C D E E C E |
| Pink | A C D E E C B A |
| Orange | A C D E E D A A |
| Yellow | A C D E B A C E |
| Light Green | A C D E B A C B A |
| Dark Green | A C D E B A D A A |
| Light Blue | A C D B C A A C E |
| Dark Blue | A C D B C A A C B A |
| Purple | A C D B C A A D A A |
There is no way of knowing which is the correct interpretation, so the code is of no use for sending messages.
Back to ASCII
As mentioned previously, ASCII preserves the prefix property because every code word has the same length (7 bits in Standard ASCII, 8 bits in Extended ASCII). No code word can be a prefix of any other code word because no code word is any longer or shorter than any other. ASCII messages can therefore be parsed unambiguously, because with code words of a fixed length we automatically know how to break the code stream into words.
Back to Morse: Food for thought
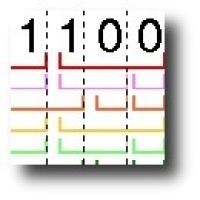
 Figure 6: Morse code. |
You can see from figure 6 that the code words used in Morse code don't possess the prefix property: the code word for 'A', for example, is a prefix of the code word for 'J', and for 'L' (and others). This leads to some interesting questions for you to ponder:
-
In transmitting Morse code messages, telegraph operators left a time gap between letters (and a longer gap between words). Why do you think they did this?
-
Can you think of any reasons behind the assignment of particular Morse code words to particular symbols?
-
What might be the difficulty for a human user in using a prefix code with no time gaps between letters or words to receive telegraph messages?
Comments
Anonymous
Nice article
Anonymous
What about self-synchronizing sequences? I first learned about these when studying disk drive encoding techniques and I find them interesting.
Lets say you have a disk drive and you want to determine if you are reading a valid 'word'?
Even more extreme, lets say you are reading a stream and the word size is variable.
These are pretty interesting topics.