This article is part of our Information about information project, run in collaboration with FQXi. Click here to read other articles on quantum computing.

If you hear in the news that someone's built a quantum computer you better block your credit card quick. All the methods that are used to encrypt your card details when you buy something online could be cracked by such a computer within seconds. And it's not only your bank details — classified information from all sources would become transparent instantly.

Many sensational claims have been made about quantum computers, but this one is true. Current encryption methods use mathematical problems that nobody knows how to crack on an ordinary computer, but which can easily be dealt with using a quantum computer. What else can we say about the power of quantum computers, compared to ordinary ones?

Cracking codes

Internet security relies on mathematical problems that are hard to solve.

A lot of theoretical effort has gone into answering this question, but it's tricky territory. RSA cryptography, a method used widely to keep our data safe, hinges on the fact that it's hard to factor large numbers (see here to find out how). If I give you the number 10, you'll be able to tell me instantly that its factors are 2 and 5. If I give you something like 62,615,533, however, your mental arithmetic will fail you.

And it's not just your mental arithmetic. Once the number to be factored is large enough, computers struggle too. "Given a number with, say, 4000 digits, all the computers in the world running for the age of the Universe will hardly get started [on factoring it]," says Richard Jozsa, a pioneer of quantum computing at the University of Cambridge.

Many other problems suffer from the same ailment as number factoring: we may have an algorithm for solving them, but the number of steps the algorithm needs to execute grows as the input to the problem becomes larger. Another example is the famous travelling salesman problem, which involves finding the shortest route that visits each of a number of cities exactly once: the more cities there are, the greater the headache.

Complexity theorists classify problems according to this growth in the number of steps (or, equivalently, the time) needed to solve them. If the growth is exponential, as is believed to be the case for the travelling salesman problem, then that’s obviously bad: exponential growth is explosive. Problems are deemed to be do-able when the number of steps needed grows like a polynomial in the size of the input: if the size of the input is then the number of steps needed grows in proportion to or or for some other natural number That growth can still be pretty fast (consider ), but complexity theorists deem it tame. "Polynomial time is a mathematical model for feasible computing," explains Jozsa. "If it doesn’t run in polynomial time, we think of it as uncomputable in practice."

Number factoring is believed to be uncomputable in this sense: nobody knows a polynomial-time algorithm that would run on the kind of computers we have today. This is where quantum computing triumphs. In 1994 the mathematician Peter Shor came up with a quantum algorithm that would run, not only in polynomial time, but in relatively fast polynomial time, involving an exponent as small as 3. The algorithm uses the maths of number theory to turn the factoring problem into one of recognising periodic patterns within certain mathematical functions — and pattern recognition is what quantum computers are good at.

Something similar goes for all other cryptography methods in use today, including, for example, elliptic curve cryptography: quantum computers can crack them with ease.

That looks good for quantum computing, but in this field few things are certain. "In complexity theory it's notoriously difficult to prove that a given task cannot be solved in polynomial time," says Jozsa. "That's an embarrassing fact." Only because nobody knows of a polynomial-time algorithm for number factoring, this doesn't mean that there isn't one, waiting to be discovered. "It's not at all out of the question that some bright number theorist will come along next week and do it," says Jozsa. "That will be a bit of a dampener for quantum computing."

Complex complexity

But what about other problems? Can quantum computing outstrip classical computing on problems that are verifiably harder than number factoring? To answer this question we first need to know what we mean by "harder", which brings us to the hierarchy of complexity classes mathematicians have come up with. First there are the "easy" problems, those for which we have polynomial-time algorithms (for ordinary computers), which together form a class called P. Then there is a class of problems for which we don't have a polynomial-time algorithm, but for which we can easily check (in polynomial time) whether a proposed solution is correct. That class is called NP. Number factoring is part of the NP class. While factoring a large number is very time-consuming, multiplying two supposed factors of a number to check whether they really are factors is comparatively quick. The difference arises because multiplying two numbers involves one "act of multiplication", while factoring might require lots and lots of trial divisions.

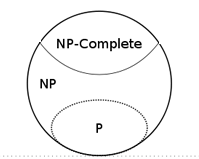
The complexity hierarchy (as it is thought to look). Image: Behnam Esfahbod.

Within the NP class, there are problems that are thought to be particularly difficult — these are called NP-complete. (The travelling salesman problem is an example.) Above the NP-complete problems there are many more complexity classes which we won't even mention here.

Number factoring is definitely in the NP class, but people don't believe it's in the NP-complete class. Since quantum computing can beat classical computing on number factoring, the next question is what happens when we go up a step in the hierarchy, to NP-complete problems. One of the sensational claims that is sometimes made about quantum computing is that it can solve these exceedingly hard NP-complete problems in the blink of an eye. But that claim is over-ambitious. "We don't know if we can solve an NP complete problem with quantum computing — in fact, we don't think we can," explains Jozsa.

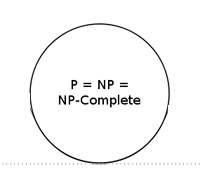
The complexity hierarchy as it would look if P=NP. Image: Behnam Esfahbod.

At this point we should acknowledge the central burning issue of complexity theory: that none of this can be proven. Not only do we not know whether quantum computers can solve NP complete problems efficiently, we don't even know that ordinary computers can't solve them efficiently. Just as there may be a polynomial-time algorithm to factor numbers which hasn't been discovered yet, so there may also be polynomial-time algorithms for other NP problems, including NP complete ones. If there are, then our hierarchy of classes collapses: the P class, the NP class and the NP complete class turn out to be one and the same. If you can prove or disprove that P equals NP, you will win yourself a million dollars from the Clay Mathematics Institute: it's deemed one of the seven most intriguing open questions in maths.

So what will quantum computers do?

If the theory leaves us on shaky ground, what can we say about practical uses of quantum computing? Problems in the P class might be "easy" in a theoretical sense, but they can still take a very long time to solve. Can quantum computing help here?

The answer is yes. An example is a "needle-in-a-haystack" problem that involves searching large and unordered data bases for a particular piece of information. Imagine, for example, searching a telephone book with entries, not for a particular person, but for a particular phone number. It’s a time consuming task because unlike the names in the book, which are ordered alphabetically, the numbers come in no particular order. A classical computer has no choice but to look at the entries one by one, so in the worst case, when the number it is looking for doesn’t exist or is the last entry, it’ll need operations. A quantum computer can perform the task using only operations. This might not seem like a huge speed-up, but when is large it can be considerable: if for example, we are talking a thousand operations on a quantum computer versus a million on an ordinary one.

Molecules are made up of many particles that are all subject to the laws of quantum mechanics.

Another very exciting application of quantum computing will be in chemistry, biology and medicine. If you are trying to understand a molecular system, for example in order to design a new drug, it's a good idea to simulate its behaviour on a computer. The trouble is that molecules are made up of many particles that are all subject to the laws of quantum mechanics. As we mentioned in a previous article, the information needed to describe the quantum state of a system of many parts grows exponentially with the number of parts, making calculations hard. "It's exponentially complicated," says Jozsa. "It turns out that even for relatively small molecules, the best classical computers are still too weak to simulate the quantum dynamics, whereas on a quantum computer we [could do it]."

Cryptography would also benefit from quantum computers. For example, since a quantum state changes when it is observed, it is possible to design ways of ascertaining whether a person has eavesdropped on a message. Using that method people can send each other encryption keys — strings of symbols that are used to encrypt and decrypt messages — and be sure they'll be alerted straight away if someone has intercepted the key. "Actual devices for doing this exist because they require no more than a few [qubits], and therefore are within the scope of current quantum technology" says Jozsa. The method was first put in public practice all the way back in 2007 when it was used to secure the transfer of votes in an election in Geneva, Switzerland. However little we might be able to say about the advantages of quantum computing from a theoretical stand point, at least we know there's some compensation for devastating our encryption methods.

But how do quantum computers actually work? And how far away are we from having a fully functional quantum computer? To find out, read the following articles:

• How does quantum computing work?
• Quantum computing: Some (not so) gruesome details (for a little more, well, detail)
• Do quantum computers exist?

About this article

Richard Jozsa

Marianne Freiberger is Editor of Plus. She would like to thank Richard Jozsa, Leigh Trapnell Professor of Quantum Physics at the University of Cambridge, for his extremely helpful, very patient and generally invaluable explanations.