Elliptic cryptography

Elliptic curves are a very important new area of mathematics which has been greatly explored over the past few decades. They have shown tremendous potential as a tool for solving complicated number problems and also for use in cryptography.

In 1994 Andrew Wiles, together with his former student Richard Taylor, solved one of the most famous maths problems of the last 400 years, Fermat's Last Theorem, using elliptic curves. In the last few decades there has also been a lot of research into using elliptic curves instead of what is called RSA encryption to keep data transfer safe online.

Public and private

Maths is keeping your data safe.

Elliptic curve cryptography, just as RSA cryptography, is an example of public key cryptography. The basic idea behind this is that of a padlock. If I want to send you a secret message I can ask you to send me an open padlock to which only you have the key. I then put my message in a box, lock it with the padlock, and send it to you. The good thing about this approach is that the message can be sent over insecure channels — even if someone intercepts the box, they don't have the key — and that we don't both need a key to the box. You could even get lots of people to send you secret messages in this way, without ever having to give away a single key.

In public key cryptography messages are encrypted using particular pieces of mathematical information, which constitute the public key — that's the open padlock and performing the encryption is like snapping the padlock shut. Decryption is only possible using a mathematical private key, which is next to impossible to determine if you only know the public key.

In RSA cryptography the public key involves a natural number which is used by computers to encrypt messages. To decrypt a message, you need to know the factors of If is very large, then factoring it takes such a large amount of computing power that breaking the code is practically impossible. Only people (or, realistically, computers) in possession of the private key — the factors of — can decrypt the message easily. (You can find out more about RSA here.)

Elliptic curves

Elliptic curve cryptography is based on the difficulty of solving number problems involving elliptic curves. On a simple level, these can be regarded as curves given by equations of the form

where and are constants. Below are some examples. In each case the graph shows all the points with coordinates , where and satisfy an equation of the form shown above.

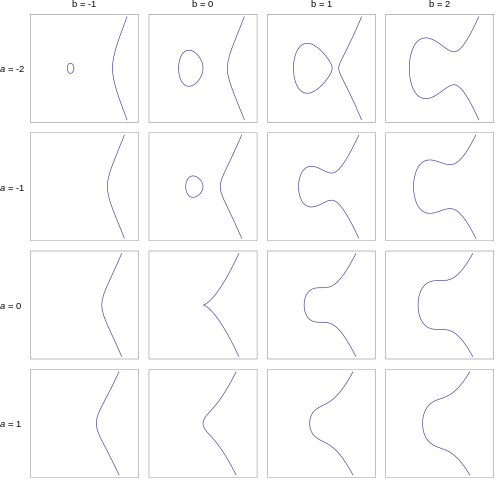
The elliptic curves corresponding to whole number values of a between -2 and 1 and whole number values of values of b between -1 and 2. Only the curve for a = b = 0 doesn't qualify as an elliptic curve because it has a singular point.

For the sake of accuracy we need to say a couple of words about the constants and For an equation of the form given above to qualify as an elliptic curve, we need that This ensures that the curve has no singular points. Informally, it means that the curve is nice and smooth everywhere and doesn't contain any sharp points or cusps. In the examples above the constants and were chosen to be whole numbers between and and and respectively. But in general they can also take on other values. (For uses in cryptography and are required to come from special sets of numbers called finite fields). You can find out more about elliptic curves in this article.

Adding points

Given an elliptic curve, we can define the addition of two points on it as in the following example.

Let’s consider the curve

and the two points and which both lie on the curve. We now want to find an answer for which we would also like to lie on the elliptic curve. If we add them as we might vectors we get – but unfortunately this is not on the curve. So we define the addition through the following geometric steps.

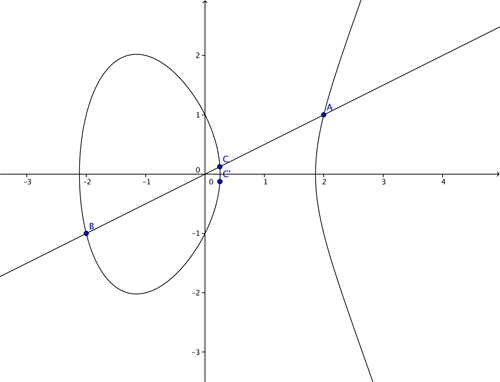
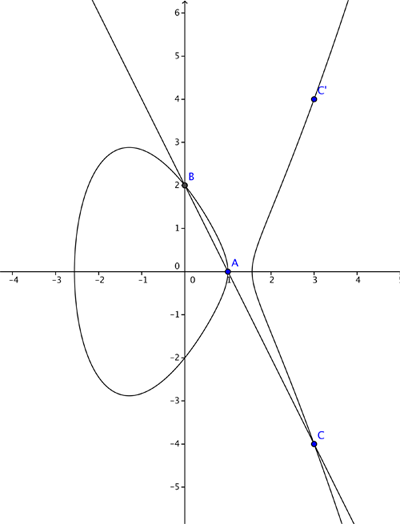
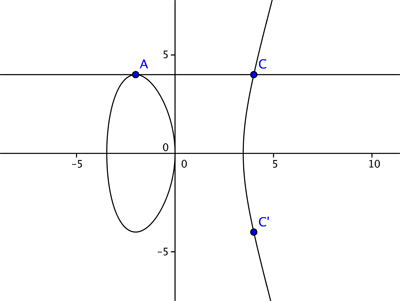
We join up the points and with a straight line. This line generally intersects the curve in one more place, We then reflect the point in the -axis.

We declare this new point, to be the sum of and So

In our example this means that

Trying another example,

(shown below), with and we have and . Therefore

We also need a definition for the sum when to understand what we mean by In this case we take the tangent to the curve at the point , and then as before find the intersection of this tangent line and the curve, before reflecting the point. This is probably easier to understand with another graph:

Here we use the elliptic curve

and consider the point We have drawn the tangent to the curve at which intersects the curve at a second point Reflecting in the - axis gives Therefore we say or

It’s now possible to define what we mean by for any point on the curve and any natural number

and so on.

The only situation in which our definition of doesn’t work is when is the reflection of in the -axis (which in the case where means that itself lies on the -axis). In this case, the line we use to define the sum is vertical and there isn’t a third point at which it meets they curve.

We can get around this problem by adding an extra point to the usual plane, called the point at infinity and denoted by To make the addition work for our exceptional situation we simply define For any point we also define — so with our new notion of addition, the point plays the same role as the number in ordinary addition.

It turns out that, given two points and on an elliptic curve, finding a number such that (if it exists) can take an enormous amount of computing power, especially when is large. Elliptic curve cryptography exploits this fact: the points and can be used as a public key, and the number as the private key. Anyone can encrypt a message using the publicly available public key (we won’t go into the details of the encryption method here), but only the person (or computer) in possession of the private key, the number can decrypt them.

NSA and hacking data

Elliptic curve cryptography has some advantages over RSA cryptography – which is based on the difficulty of factorising large numbers – as less digits are required to create a problem of equal difficulty. Therefore data can be encoded more efficiently (and thus more rapidly) than using RSA encryption. Currently the digital currency Bitcoin uses elliptic curve cryptography, and it is likely that its use will become more widespread as more and more data is digitalised. However, it's worth noting that as yet no-one has proved that it has to be difficult to crack elliptic curves – there may be a novel approach which is able to solve the problem in a much shorter time. Indeed many mathematicians and computer scientists are working in this field.

Government digital spy agencies like the NSA and GCHQ are also very interested in such encryption techniques. If there was a method of solving this problem quickly then overnight large amounts of encrypted data would be accessible – and for example Bitcoin currency exchange would no longer be secure. It also recently transpired that the NSA has built "backdoor" entries into some elliptic curve cryptography algorithms which have allowed them to access data that the people sending it thought was secure. Mathematics is at the heart of this new digital arms race.

Further reading

To find out more about the development of codes, including modern elliptic curve cryptography, and their links to mathematics, the book by William Stein, Elementary Number Theory: Primes, Congruences and Secrets is an good starting place. Numberphile have also covered the NSA's attempts to circumvent elliptic curve cryptography in one of their ever excellent videos.

About the author

Andrew Chambers has an MSc in mathematics and is a teacher at the British International School Phuket, Thailand. He has written news and features articles for the Guardian, Observer and Bangkok Post, and was previously shortlisted for the Guardian's International Development Journalist of the Year Awards. Combining his love of both writing and mathematics, his website ibmathsresources.com contains hundreds of ideas for mathematical investigations (and some code breaking challenges) for gifted and talented students.