Add new comment

Outer space: Archimedean ice cream cones

There are many situations in the natural world where having lots of surface area is advantageous and natural selection will reward you for it. We think of the branchiness and leafiness of trees which have developed fractal structures to maximise the area of their light and nutrient gathering surfaces compared to their weight or volume. This is one of the reasons why natural curves and shapes are frequently jagged while humanly engineered one, like aerofoils and car bodies, are smooth — they are optimising something else.

What are the optimal dimensions?

We see other situations where the aim might be to minimise the surface area enclosing a given volume. For example, if we are manufacturing tin cans for baked beans then we want to minimise the area of tin needed to enclose a given volume, $V$ , of beans. Suppose our tin has a circular top and bottom of radius $r$ and is of height $h$ . Then its total surface area (two circles of radius $r$ and a cylinder of perimeter $2\pi r$ and height $h$ ) is

$A=2\pi r^{2}+2\pi rh.$

Since the volume enclosed by the can is $V=\pi r^{2}h$ we can rewrite our area formula by substituting for $h=V/\pi r^{2}$ as

$A=2\pi r^{2}+2V/r.$

Our volume is fixed so to find the minimum area of tin we calculate the derivative

$dA/dr=4\pi r-2V/r^{2}$

and set it to zero (and check that $d^{2}A/dr^{2}>0$ so it is indeed a minimum).

Hence we see that we need

$V=2\pi r^{3}$

and so, since $V=h\pi r^2$ , we need $h=2r$ for the most economical tin can: its height equals its diameter.

You might like to check that if you were making a cylindrical mug — so there is no top — then the best proportion is flatter, with $h=r$ . If you look around the supermarket shelves you will find some cans that have the optimal diameter equals height shape but many do not. Perhaps they just want to look different and stand out on the shelves?

Incidentally, if we had changed our problem to find the shape that maximised the volume enclosed by a given area, can you guess what the answer would be?

Finally, as it’s the ice cream cone eating season, lets ask what is the most economical shape of ice cream cone from the point of view of cone makers. As Archimedes first taught us in 225BC, if the top of the open cone is a circle of radius $r$ and its height to the apex is $h$ , then the volume of ice cream enclosed by a full cone is

$V=\frac{1}{3}\pi r^{2}h,$

while its surface area is

$A=\pi r\sqrt{r^{2}+h^{2}}.$

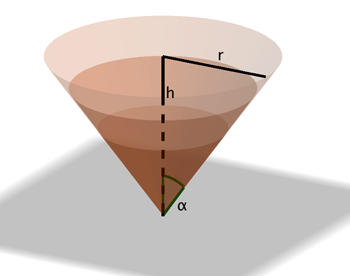
Now as in our problem of the tin can, we substitute for $h=3V/\pi r^{2}$ in the formula for $A,$ calculate $dA/dr$ , and set it equal to zero. We have

$dA/dr=\pi \left[ r^{2}+\frac{9V^{2}}{\pi ^{2}r^{4}}\right] ^{1/2}+\frac{\pi r }{2}\left[ r^{2}+\frac{9V^{2}}{\pi ^{2}r^{4}}\right] ^{-1/2}\left[ 2r-\frac{ 36V^{2}}{\pi ^{2}r^{5}}\right].$

Setting this equal to zero, the result is

$r^{3}=3V/\pi \sqrt{2}=r^{2}h/\sqrt{2}$

and so the optimal height to radius ratio for the best ice cream cone is $h/r=\sqrt{2}.$ Therefore, since $r/h=1/\sqrt{2}$ is the tangent of the angle $\alpha$ that the vertical through the point of the cone makes with the side, this angle is $\tan ^{-1}{(1/\sqrt{2})} = 0.6$ , measured in radians. This corresponds to $35.26^{\circ }$ or $35^{\circ }15^{\prime }$ .

In some sense this is the most economical cone.

The differently shaded regions in the image above indicate three cones of different volumes, but each with a value of $\alpha$ that guarantees the minimal surface area for its volume. The Geogebra applet below shows all the cones of a given volume (which we have arbitrarily chosen to be 6). You can use the slider on the top left to change the radius of the cone, which also changes its height accordingly. To keep the volume constant, the point A needs to lie on the black curve. When A=D the surface area of the cone is at its minimum. As we have calculated, this happens when the angle at the apex of the cone, between the vertical and a side, is approximately 35 degrees.

Plus.Maths.org

Outer space: Archimedean ice cream cones

Filtered HTML