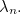Metallic sequences
Suppose we have an infinite sequence
![\[ a_1,a_2,a_3,a_4,... \]](/MI/43a368440125e57cff73358f7c062431/images/img-0001.png) |
and that for all 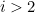 we have
we have
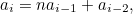 |
(1) |
where 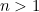 is a positive integer.
is a positive integer.
In the main article we claimed that in this case the ratio of successive terms of the sequence converges to the metallic mean 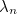 . We’ll now give you a justification of this claim. Recall that
. We’ll now give you a justification of this claim. Recall that
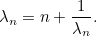 |
(2) |
Substituting the expression given by this equation for the 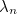 in the denominator on the right hand side of the same expression gives
in the denominator on the right hand side of the same expression gives
![\[ \lambda _ n=n+\frac{1}{n+\frac{1}{\lambda _ n}}. \]](/MI/43a368440125e57cff73358f7c062431/images/img-0007.png) |
Another substitution gives
![\[ \lambda _ n=n+\frac{1}{n+\frac{1}{n+\frac{1}{\lambda _ n}}}. \]](/MI/43a368440125e57cff73358f7c062431/images/img-0008.png) |
Continuing on in this vein, it is not too hard to prove that 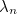 is equal to the infinite continued fraction
is equal to the infinite continued fraction
![\[ n+\frac{1}{n+\frac{1}{n+\frac{1}{n+...}}}. \]](/MI/43a368440125e57cff73358f7c062431/images/img-0009.png) |
(You can find out more about continued fractions here.)
Now back to our sequence. The ratio of successive terms is
![\[ \frac{a_ i}{a_{i-1}}. \]](/MI/4ead4f838439a65eb7bb2abad3c138ff/images/img-0001.png) |
By equation (1) this is equal to
![\[ \frac{a_ i}{a_{i-1}}=\frac{na_{i-1}+a_{i-2}}{a_{i-1}}=n+\frac{a_{i-2}}{a_{i-1}}. \]](/MI/4ead4f838439a65eb7bb2abad3c138ff/images/img-0002.png) |
Now
![\[ \frac{a_ i}{a_{i-1}}=n+\frac{a_{i-2}}{a_{i-1}}=n+\frac{1}{\frac{a_{i-1}}{a_{i-2}}}. \]](/MI/4ead4f838439a65eb7bb2abad3c138ff/images/img-0003.png) |
Applying equation (1) to the term 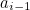 we get
we get
![\[ \frac{a_ i}{a_{i-1}}=n+\frac{1}{\frac{na_{i-2}+a_{i-3}}{a_{i-2}}}=n+\frac{1}{n+\frac{a_{i-3}}{a_{i-2}}}. \]](/MI/4ead4f838439a65eb7bb2abad3c138ff/images/img-0005.png) |
You can see the picture: continuing to make substitutions according to equation (1), we end up with a finite continued fraction expression for 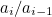 of the form
of the form
![\[ a_{i}/a_{i-1}=n+\frac{1}{n+\frac{1}{n+\frac{1}{...+\frac{a_1}{a_2}}}}. \]](/MI/681fd03b76daed6b3e9d7be35f94976b/images/img-0002.png) |
Letting 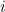 tend to infinity we can then prove that the ratio of successive terms in the sequence converges to infinite continued fraction
tend to infinity we can then prove that the ratio of successive terms in the sequence converges to infinite continued fraction
![\[ n+\frac{1}{n+\frac{1}{n+\frac{1}{n+...}}}. \]](/MI/681fd03b76daed6b3e9d7be35f94976b/images/img-0004.png) |
Which, as we have sketch-proved above, is equal to