
Metallic numbers: Fibonacci and more
In the first part of this article we introduced an infinite family of numbers, called metallic means, of which the famous golden ratio is a member. We'll now look at properties that are shared by all the metallic numbers (and one that isn't).
Fibonacci and beyond
Let's first focus on the golden ratio $\phi$. Because $$1+\phi=\phi^2,$$ we have that \begin{equation}\phi^{n-2}+\phi^{n-1}=\phi^n\end{equation} for any integer $n\geq 2.$ This just comes from multiplying the equation through by $\phi^{n-2}.$ Now consider the sequence of powers of $\phi,$ \begin{equation}1, \phi, \phi^2, \phi^3, \phi^4, \phi^5,...\end{equation} Because of equation (1) we see that any term in this sequence (except the first two) is the sum of the two previous ones. If this looks familiar, it's probably because the famous Fibonacci sequence also satisfies this relation: $$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...$$ In sequence (2) the ratio between any term and its predecessor is exactly equal to $\phi$. In the Fibonacci sequence the ratios aren't exactly equal to $\phi$, but they converge to $\phi$ as the sequence progresses. Written in decimals, and rounded to four places, the ratios are $$1, 2, 1.5, 1.6666, 1.6, 1.625, 1.6154, 1.619, 1.6176, 1.6181, 1.618...$$
In fact this is true for any sequence in which any term is the sum of the two previous ones: the ratios of successive terms converge to the golden ratio.
Now on to the silver ratio. Since $$1+2\sigma=\sigma^2,$$ we have that for any $n\geq 2$ $$\sigma^{n-2}+2\sigma^{n-1}=\sigma^n.$$ This means that, for $n>2$, the $nth$ term in the sequence $$1, \sigma, \sigma^2, \sigma^3,\sigma^4, ...$$ is equal to twice the $(n-1)st$ term plus the $(n-2)nd$ term. The silver ratio has its own analogue to the Fibonacci Sequence, called the Pell sequence: $$0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860,...$$ The Pell Sequence is similar to the Fibonacci sequence in that the ratio of successive terms tends to the silver ratio as the sequence progresses. This is true for any sequence in which every term (apart from the first two) is equal to the sum of twice the previous term and the term before that. Analogous results hold for any other metallic ratio $\lambda_n$. In this case , for $n>2$, the $nth$ term in the sequence $$1, \lambda_n, \lambda_n^2, \lambda_n^3,\lambda_n^4, ...$$ is equal to $n$ times the $(n-1)st$ term plus the $(n-2)nd$ term.As before, the ratio of successive terms of any other sequence for which this relationship holds converges to $\lambda_n$ as the sequences progresses (you can see a sketch proof of this here, which ventures into the exciting world or continued fractions). We will leave it as an exercise for you come up with sequences that correspond to the Fibonacci sequence for general $\lambda_n$.
Metallic rectangles
A golden rectangle is a rectangle whose side lengths have the ratio $\phi$ (or $1/\phi$ depending on which way around you take the ratio). If, in a golden rectangle, you form a square on one of the shorter sides and then remove that square from the original rectangle, the rectangle that is left is also a golden rectangle.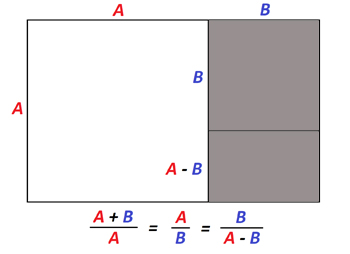
The shaded rectangle is itself a golden rectangle. (We leave it to you to prove that this is true by working out that A/B=B/(A-B).)
You can then repeat this process to form an even smaller golden rectangle, which in turn can be turned into a smaller one, and so on, indefinitely.
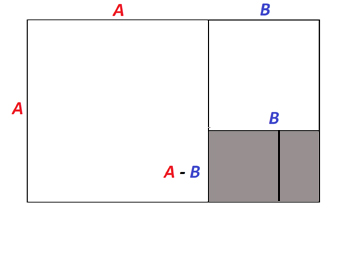
The shaded rectangle is itself a golden rectangle.
In this case, if you form a square on the shorter side, and then place another square of the same side length right next to it, and then remove both those squares, what is left is also a silver rectangle. As with the golden rectangle, you can repeat this process indefinitely, forming a sequence of ever smaller silver rectangles.
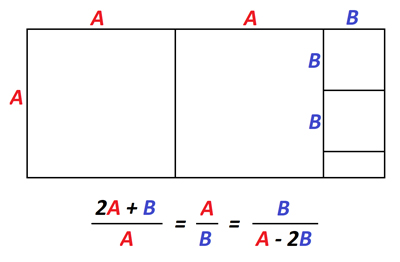
Successive metallic ratios have analogous associated rectangles, which through a similar process can be shown to reproduce a smaller version of themselves.
Metallic spirals
Given a golden rectangle, if you draw quarter circles in successive squares, you get what is known as the golden spiral.
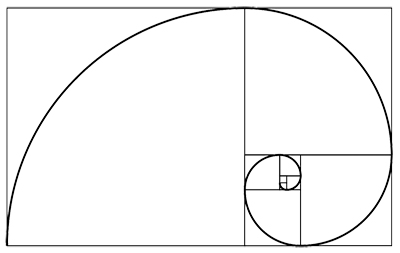
For the silver ratio we can construct a spiral-like shape by arranging the squares within the rectangle as shown below:
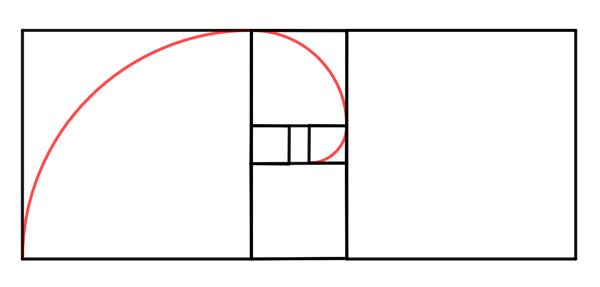
The spiral for the metallic ratio $\lambda_3$ is constructed as follows:
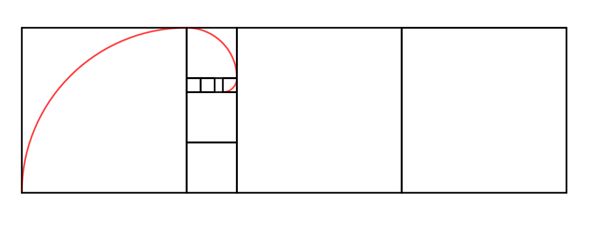
Similarly, one can construct a spiral shape for $\lambda_n$ for any $n$. These shapes are approximations logarithmic spirals and they are described in polar coordinates as
$$r=(\lambda_n)^{\frac{2}{\pi}\theta}.$$ for the varying values of $\lambda_n.$In the Geogebra interactive below you can play with logarithmic spirals corresponding to various values of $n$.
Logarithmic spirals have the interesting property of self similarity, in that the shape of the spiral remains similar as you zoom in and out. We can see from the equation that when $\theta$ increases by an an angle of $\pi/2$, $r$ increases by a factor of $\lambda_n$.
The media often represents the golden spiral as having a special place in nature. However, many of the spirals we see in nature are general logarithmic spirals which do not always correspond to the golden ratio in particular.

A low-pressure system swirls off the southern coast of Iceland Credit: NASA.

Artist's impression of the Milky Way. Credit: NASA.
Not necessarily metallic polygons
The figure below shows a regular pentagon. The ratio between the sides of the triangle indicated is exactly $\phi$. This is true for any regular pentagon, no matter how large or small.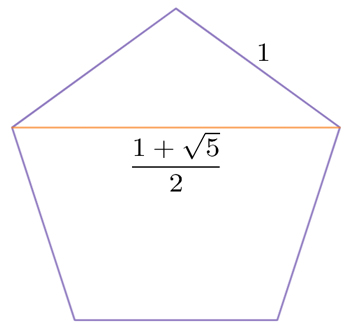
Something similar occurs with the regular octagon and the silver ratio.
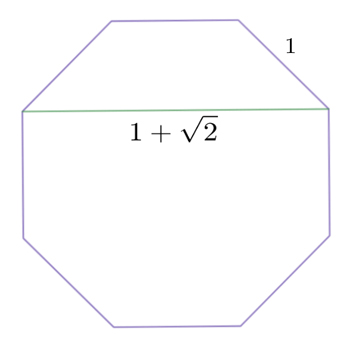
However, interestingly, despite the numerous common properties of the metallic ratios, no other metallic ratio appears to be manifest in other regular polygons.
But either way — the next time someone tells you about the beauty and elegance of the golden ratio, you can introduce them to the whole family of metallic means.
About the authors
Gokul Rajiv and Yong Zheng Yew are two former high-school level students in Singapore who happened to explore the idea of metallic means in a project and found it interesting enough to share.

Comments
Fred Brackx
Golden, silver and metallic spirals and, more generally, plane curves consisting of successive circle arcs, are nice examples of curves which are $C_1$ but not $C_2$, since they show continuous tangent lines, but piecewise constant, whence non-continuous, curvature. On the contrary logarithmic spirals, where the radial distance r is an exponential function of the polar angle, are $C_{\infty}$ curves.
Writing that "Similarly, one can construct a spiral for $\lambda _ n$ for any $n$. These are logarithmic spirals ..." may cause some confusion. Better were to write that metallic spirals are very good approximations to logarithmic spirals (and vice versa).
Chris G
How might the Pell sequence model rabbit population growth?
Start off with 1 pair which after a month (or whatever) gives birth to 2 pairs. After another month, 1 of those pairs then gives birth to 2 pairs, but the other is more fecund and produces 3, making 5 altogether. Next month the 2 pairs each respectively produce a 2 and a 3, while the 3 produce a 2 and a 2 and a 3, resulting in 12 altogether. And so on. (It's relatively easy to visualise this process using say one dot linked by lines down the page to n other dots to represent one pair giving birth to n others.) Fast eh? Might be a better model for virus than rabbit reproduction.
How might the Pell sequence be Lucasated, that is what sequence would more faithfully reflect the powers of the Silver ratio just as the Lucas sequence does with the Golden?
1 1 3 7 17 41 99 239 577 . . . (OEIS A001333 "Numerators of continued fraction convergents to √2")
Starting with the second number as index 1, 41 for example is at index 5 and is much closer to ((1+√2)^5)/2 than the corresponding number in the "standard" Pell in the article, though admittedly you have to divide by 2.
Prakash
Excellent approach at this level. Well done. Keep it up
Teller M
Nice overview. FYI the bronze mean appears in the tridecagon. 5th mean appears in a 29-gon. 6th mean appears in a tetracontagon (40-gon). 8th mean appears in a heptadecagon. Not as a ratio of side to diagonal but as a ratio of line segments. The resultant trigonometric expressions are shown on the wikipedia page (https://en.wikipedia.org/wiki/Metallic_mean) and https://tellerm.com/math/metal_ngons/.
Christian Wolird
The golden and Silver ratios are the only metallic ratios which can be expressed as ratios between the side-lengths and/or diagonal lengths of regular polygons. We did this finding the cyclotomic zeros of some polynomials that, in a way, matched up with metallic ratios. If you're interested in the details, the full paper is here: https://arxiv.org/abs/1910.10325 It was also published in "Integers": http://math.colgate.edu/~integers/v40/v40.pdf