
The Abel Prize 2024: Michel Talagrand
This year's Abel Prize has been awarded to Michel Talagrand. The Abel Prize is one of the highest accolades in mathematics. Awarded annually by the Norwegian Academy of Science and Letters, it comes with a prize money of 7.5 million Norwegian Kroner (over £550,000). It is named after the Norwegian mathematician Niels Henrik Abel.
Talagrand received the award for "his ground breaking contributions to probability theory and functional analysis, with outstanding applications in mathematical physics and statistics."
Start in the casino
Probability theory has its roots in the 16th and 17th century and was originally inspired by gambling. If you are betting on the roll of a die, it helps to know that each number has the same chance of being rolled, so it doesn't matter which one you bet on (as long as the die isn't wonky).
When two dice are rolled and you bet on the sum of the outcomes, it's useful to know that you're better off betting on a 7 than a 2. That's because there's a total of six number combinations that add up to 7, but only one that adds up to 2. This is illustrated in the histogram below, which shows the distribution of possible outcomes of this game.
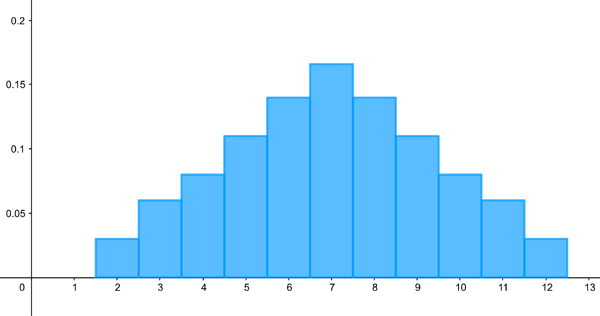
A histogram visualising the distribution associated to rolling two dice and adding up the results. The most likely result is 7 and the least likely results are 2 and 12. The numbers on the vertical axis represent proportions. For example, in 6 of the 36 possible outcomes we end up with a 7. This corresponds to a proportion of 6/36=0.16.
While gambling served as initial inspiration for the development of probability theory, it eventually became clear that all sorts of random processes exhibit some form of regularity, and that the theory can help us understand this.
As an example, imagine you want to know the distribution of heights of people in the UK. You can't measure everyone, so you randomly pick 100 people and measure their height. If you plot a histogram of your measurements, the shape you get will approximate the bell shape of the normal or Gaussian distribution (named after the mathematician Carl Friedrich Gauss).
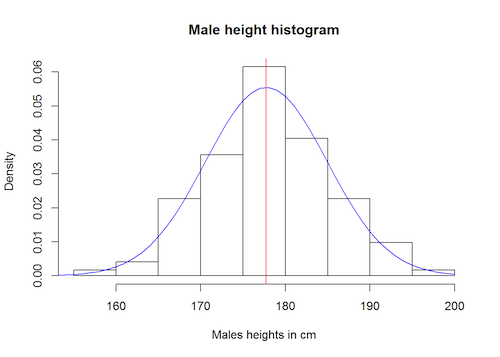
A histogram showing the heights of a sample of men. It approximates the shape given by the Gaussian distribution shown in blue. The numbers on the vertical axis again give the proportions, or density. Figure: OpenIntro, CC BY-SA 3.0 DEED.
The peak of the curve represents the height that most people have, which also happens to be the average, or mean, height. The fact that the curve slopes off to the sides reflects that very small and very tall heights become increasingly less likely as they become more extreme. The width of the curve reflects the variability of heights in the population. Your histogram will approximate the Gaussian bell curve for pretty much any random sample of people you might pick, as long as it’s large enough. The more people there are in your sample, the closer the approximation will be.
Astonishingly, there are also countless other phenomena that follow a Gaussian distribution, from people's shoe sizes to blood pressure measurements. You can even link this back to our example of rolling dice: if you roll a large number of them and add up the results, the distribution you get also approximated a Gaussian bell curve. The mean and the width of the curve will be different in each of our examples, but the overall shape of the curve, as well as the mathematical formula which describes it, will be the same — you can find out more here.
Bounding extremes
Talagrand's work in probability theory goes further in putting bounds on the uncertainties that life and nature throw at us. One celebrated piece of work concerns what are called Gaussian processes. In the example above we were dealing with a single random variable — a quantity, such as people's height, that can take on a range of different values and does so in an unpredictable fashion.
Gaussian processes describe situations where there are many, possibly infinitely many, random variables, each of which follows a normal distribution, and which can be correlated in a certain way. An example might come from measuring the concentration of a pollutant in the air at many different points in time. The possible outcomes of each individual measurement may follow a normal distribution and measurements taken close to each other in time are probably going to be similar.
Knowing that the situation can be described using the mathematical concept of a Gaussian process is useful — for example, it allows you to calculate the average value your measurements might take over a range of times.
A different, but equally important, question concerns not averages but extremes. What are the largest or smallest values we can expect to see in a Gaussian process? To answer this question you need to reach for the work of Talagrand. Building on results by Xavier Fernique and Richard Dudley, Talagrand's celebrated theory of generic chaining provides sharp bounds on how large or small those extreme values can be expected to become. This information may well be crucial when it comes to deciding what to do regarding the phenomenon you're describing. If it's air pollution, and predicted extremes are very large, you might want to do something drastic.
Concentration of measures
Another important contribution of Talagrand concerns something called the concentration of measures and is best explained by going back to gambling. When you roll a fair die once, the knowledge that each number has an equal probability of 1/6 of being rolled is rather abstract: it's hard to pin-point exactly what it means.
When you roll the die 6000 times, however, this knowledge tells you that the number of 1s you will get is most likely to be in the region of 1000. That's because there are many more sequences of 6000 rolls that have around a thousand 1s in them than there are sequences that have significantly fewer or more 1s. The number of 1s is concentrated on 1000. (The same is true for all the other numbers 2 to 6.)
This insight is an illustration of the law of large numbers and it's incredibly useful. If you run a casino, for example, it can help you project your long-term gain or loss in games involving dice, even though you can't predict the outcome of a single game.
When it comes to random processes that aren't as clear-cut as rolling a fair die, results regarding the concentration of probabilities are much harder to come by. Here, Talagrand delivered an "amazing tour de force" as the Abel Prize citation puts it, proving results about concentrations , that hold in more general settings. The work illustrates the idea that the interplay of many random events can, counter-intuitively, lead to outcomes that are more predictable, and gives estimates for the extent to which the uncertainty is reigned in.
Unusual magnets and artificial intelligence
Since the foundations for probability theory were first laid, its areas of application have spread far beyond gambling, or even dealing with population statistics such as people's height. An interesting example is statistical physics, which bridges the gap between the macroscopic world we can directly observe and the microscopic world made up of atoms and molecules whose behaviour we can't easily keep track of.
Statistical physics does this by focussing on the bulk, rather than individual, behaviour of microscopic components. The temperature of a material, for example, is the average kinetic energy of all the atoms and molecules that make it up.
Since statistics and probability theory are inextricably linked, it's not surprising that Talagrand made important contributions to statistical physics too. One area of interest concerns disordered materials known as spin glasses. An example is a metal alloy which has some iron atoms mixed into a grid of copper atoms. Each iron atom behaves like a tiny magnet, also called a spin, and is affected by other iron atoms nearby. In an ordinary magnet all spins line up to point in the same direction, but in a spin glass some pairs of spins want to point in the same direction, while others want to point in opposite directions — the spins are frustrated as physicists put it. The question is, how do the spins find an optimal configuration, one in which the energy of the system is minimised?
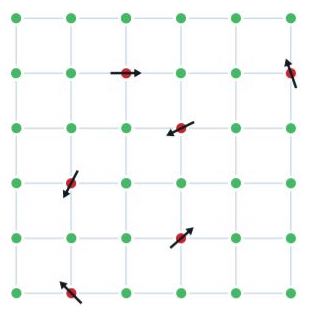
A spin glass is a metal alloy where (for example) iron atoms (red) are randomly mixed into a grid of copper atoms (green). Each iron atom behaves like a small magnet, or spin, and is affected by nearby iron atoms. Image: Johan Jarnestad, Royal Swedish Academy of Sciences. Taken from the Nobel Prize website.
Major advances in this area were made by Giorgio Parisi, who received part of the 2021 Nobel Prize for Physics for his work on disordered and random phenomena. In particular, Parisi suggested a formula for the free energy of a spin glass system, assuming the system can be accurately described by a certain type of mathematical model.
What Parisi didn't do was provide a proof that the formula was indeed correct. One half of this proof was delivered by the mathematical physicist Francesco Guerra, who showed that the free energy couldn't be bigger than Parisi’s formula suggested. The other was provided by Talagrand, who in a "ground breaking article" proved that it couldn't be smaller.
What is fascinating about results concerning spin glass is that their impact is felt far beyond the study of frustrated spins in unusual materials. The mathematics involved can be applied to other disordered systems, of which there are many in the world around us. Amazingly, it is also relevant to deep learning algorithms, which power the advances in artificial intelligence we have seen lately.
The right point of view
In this article we touched on just a few of the contributions that Talagrand has made to mathematics and its applications. "Talagrand is an exceptional mathematician, and a formidable problem solver," says Helge Holden, Chair of the Abel Prize Committee. "He has made profound contributions to our understanding of random, and in particular, Gaussian, processes. His work has reshaped several areas of probability theory. Furthermore, his proof of the celebrated Parisi formula for free energy of spin glasses is an amazing accomplishment."

Michel Talagrand. Photo: Peter Bagde / Typos1 / Abel Prize 2024.
Talagrand was born in France in 1952 and for all his professional life was affiliated to the National Centre of Scientific Research (CNRS) in Paris. His attitude to mathematics is playful. He always works on problems he enjoys and sometimes bats them about like a cat does a mouse, switching between trying to prove that something is true to proving it's not true. "The progress comes by jumps, much like matching two pieces of a puzzle," he is quoted as saying on the Able Prize website. "This is nearly instantaneous. Now you see it, and the moment before you did not. After such progress, you may have a much clearer vision of the problem."
On his website Talagrand states that "mathematics gives you wings". This is a reference to the painting Allegory of divine wisdom by Luca Giordano. And in a section called "Become rich with my prizes" Talagrand offers money for the solutions to some is favourite maths problems.
When looking through some of Talagrand's papers we were struck by the level of insight he conveys, going beyond the technical details needed to understand a particular piece of mathematics. In his paper A new look at independence, for example, he muses on the fact that mathematics often depends on finding the right point of view: once you've found it, difficult ideas can suddenly appear simple, or "trivial" as mathematicians put it. This leads to our favourite quote from the paper:
"I must apologise should I insist too much on trivialities. Triviality is apparently in the eye of the beholder."
As people who communicate complex mathematics to non-experts, and indeed, as people who often start out as non-experts ourselves, we whole-heartedly agree!
About this article
You can find out more about Talagrand and his work on the Abel Prize website.
Marianne Freiberger is Editor of Plus