
In the last few days we've learnt about black holes and how were they first detected. But they were first predicted thanks to mathematics! On this ninth day of advent we return to our 2015 interview with cosmologist Pau Figueras, to ask him how they were predicted, and how you can describe them mathematically.
How were black holes first predicted?
Einstein published his [general theory of relativity] in late 1915, and only a few months later, in early 1916, [Karl] Schwarzschild found the first solution of the Einstein equations. [By solution we mean some values for the variables describing the curvature of spacetime and the distribution of matter that satisfy the Einstein equations.] [This solution] describes the gravitational field of a spherically-symmetric body: a black hole.
At that time it wasn't understood that that solution corresponded to a black hole. In fact even in the 30s the greatest minds of that time, [including] Einstein himself, despised the idea of a black hole because it contained a singularity, namely a place where curvature is so large that even general relativity breaks down. It took nearly 50 years to really understand what a black hole is, and this was done only in the 1960s.
General relativity asserts that massive objects curve spacetime (see door #2 to find out more). How do black holes affect the curvature of spacetime?
The strength of the gravitational field is measured in terms of the curvature. And because black holes are very massive and they are very small, their gravity is very strong and [creates] a very large curvature of spacetime.One way to characterise the curvature is something called the Schwarzschild radius: $$ R_s = \frac{2 G_N M}{c^2} $$ where $G_N$ is Newton's constant [of gravity], $M$ is mass of the object and $c$ is speed of light.
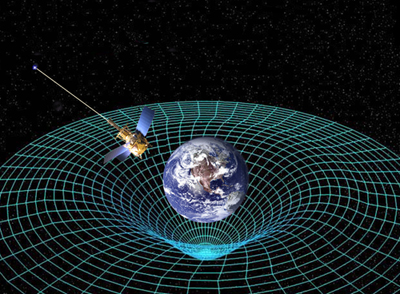
Massive bodies warp spacetime. Image courtesy NASA.
The Schwarzschild radius is, more or less, the size that a given object, with a given mass, should have in order for it to be a black hole. For instance, if we managed to concentrate all the mass of the Earth into a sphere of a radius of a few centimetres, then that object would be a black hole.
Can you characterise a black hole so simply, with just a few features, such as mass and size?
One of the reasons why black holes are so important in our understanding of general relativity is because of their simplicity – because they are made of the most fundamental building blocks of the theory, namely space and time alone. They are very simple and therefore we can understand them.
This [is in contrast to] other gravitational objects, such as stars. In order to understand a star, [as well as needing] to take into account general relativity, you also need to understand nuclear physics to account for the nuclear reactions [and] plasma physics to understand the transport of heat within the star. This gets very complicated and we are often led to study these objects within certain approximations.

Simulated view of a black hole. Image: Alain Riazuelo.
We don't have to do that with black holes because they are only made of space and time, so we have a complete understanding of them within our theory alone. We don't need any other physics. This simplicity gets translated into the fact that they are just described in terms of very few parameters.
If the black hole is static, then it must be spherical and there is only one parameter characterising the black hole, namely its mass. [However], objects in nature, like stars, rotate, so the black holes that occur in nature should have some rotation. The Schwarzschild solution was found [just] months after Einstein published his theory, but it took another 50 years to find the general solution which has rotation and is relevant to describe the black holes [we might find in] nature. This Kerr solution is described entirely by just two parameters, namely the mass and the spin of the black hole. With these two parameters you can fully characterise all black holes in nature and we don't need to make any approximations to understand those objects. This is why they are so important.
In a sense, black holes are no different than elementary particles [in particle physics] because we only need to specify a few parameters [to describe these]. The same with black holes - [they] are the elementary particles of general relativity.
You can find all Figueras' answers, in the full article, and accompanying video and podcast! And we'll uncover some mysteries of black holes with Stephen Hawking behind future doors!
This year's advent calendar was inspired by our work on the documentary series, Universe Unravelled, which explores the work done by researchers at the Stephen Hawking Centre for Theoretical Cosmology and is available on discovery+. Return to the 2020 Plus Advent Calendar.