
When trying to build an artificial intelligence, it seems a good idea to try and mimic the human brain. The basic building blocks of our brains are neurons: these are nerve cells that can communicate with other nerve cells via connections called synapses.
A single neuron consists of a body, tree-like structures called a dendrites, and something akin to a tail called an axon. The neuron receives electrical signals from other neurons through its dendrites. If the signals it receives exceed a certain threshold, then the neuron will fire: it'll send a signal to other neurons through its axon. A neuron will either fire or not fire, it can't fire just a little bit. It's an all or nothing, 0 or 1 response.
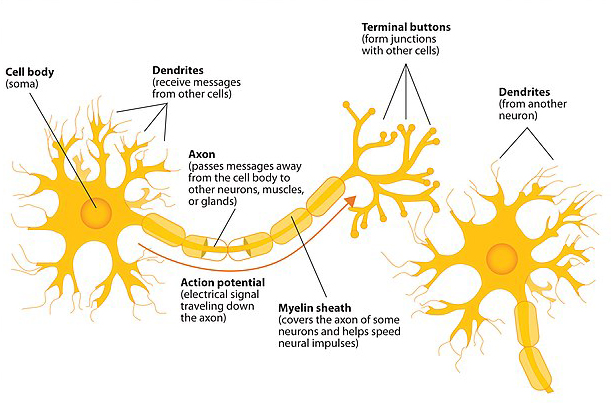
Diagram of a basic neuron and components. Image: Jennifer Walinga, CC BY-SA 4.0.
The human brain contains around 86 billion neurons and there are between 100 and 300 trillion connections between neurons. Our brains function through the impulses that travel through this vast network of neurons.
When people talk about artificial neurons they don't mean physical objects, but mathematical structures that mimic the behaviour of a real neuron, at least to some extent. Linked up to form neural networks, these mathematical objects can be represented in computer algorithms designed to perform all sorts of tasks.
So what does an artificial neuron look like? A simple example is the perceptron, which was introduced by Frank Rosenblatt in 1962. It consists of a node which corresponds to the cell body of a real neuron. The node can receive a number of inputs from other nodes, or perhaps from outside the neural network it is part of. Each input is represented by a number. If there are $n$ inputs, then we can write $X_1$, $X_2$, $X_3$, etc, for those $n$ numbers.
Once the inputs have arrived at the node they are combined to give a single number. The simplest way of doing this would be to add them all up. The next simplest thing to do is to first multiply each of the $n$ inputs by a \emph{weight} and then add up all the products of inputs and weights, giving you a \emph{weighted sum}. Multiplying an input by a small positive number means that input counts little towards the final result and multiplying it by a large positive number means it counts a lot.
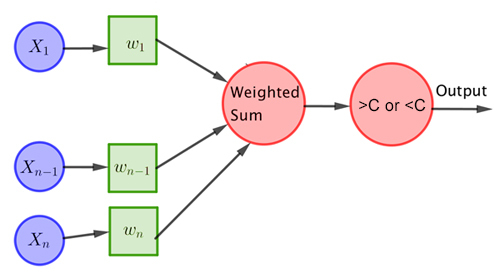
A perceptron. This diagram is an adapted version of the diagram in What is machine learning?
If the weighted sum is greater than some threshold $C$ the perceptron returns a (decision of) 1, and otherwise a (decision of) 0, corresponding to a neuron firing or not firing.
Simple as the concept of an artificial neuron may seem, networks of such neurons can perform astonishingly complex tasks — they can even "learn" how to perform these tasks all by themselves. To find out more, read the article What is machine learning?.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
