You are out on a mountain and the mist has descended. You can't see the path, let alone where it leads, so how on Earth do you find your way down to the safety of the village at the bottom of the mountain?

Never fear! Maths has come to your rescue! You can use a gradient descent algorithm – a mathematical technique for finding the minimum of smooth (i.e. differentiable) functions!

The mist is so thick that you can't see into the distance, so instead, you have to work locally. You can explore the ground very close to where you are standing and figure out which direction is downhill and head that way. That's how a gradient descent algorithm works, though instead of feeling which way is downhill with your feet and body, you can find the downhill gradient mathematically using calculus. (Exactly what the algorithm looks like depends on the problem, you can read some of the details on Wikipedia, which is also where we first came across the lovely misty mountain analogy.)

Maths can find the way!

If we are using this algorithm on a mountainside we are working our way over a two-dimensional surface. You can easily imagine this algorithm going wrong and you ending up in some local minimum where every direction is uphill and you are stuck in hole, a pit of despair halfway down the mountain and not the safety of the village at the bottom. In some mathematics problems you might be happy with a local minimum, and the gradient descent algorithm is a reliable way to find one of these. But if what you want is the global minimum, you might have to move to higher-dimensional ground.

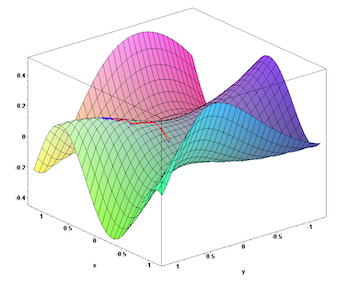
A saddle point on a surface, the red line tracing the progress of a gradient descent algorithm

On a two-dimensional mountainside you have a limited number of directions to choose from: North, South, East and West and combinations of these. But in higher dimensional spaces there are a lot more directions to try. And thankfully it turns out that you can show mathematically that you'd have to be really unlucky to end up in a place that is a local minimum in every possible direction: even if in many of the directions it looks like you are in a hole (in a local minimum), you can be almost certain that at least one of the many possible directions will lead you out downhill (which means you're at what's called a saddle point, rather than in a hole), and you can carry on moving downhill towards the safety at the bottom. The gradient descent algorithm has a really good chance of leading you to the global minimum.

We came across the gradient descent algorithm in the context of machine learning, where a neural network is trained to do a certain task by minimising the value of some optimisation function as you move over a mathematical surface. And in this case the mathematical surface equates to the space of possible configurations of the weights given to the connections between neurons in your neural network. (You can read a brief introduction to machine learning and neural networks here.) The gradient descent algorithm is often used in machine learning to find the optimal configuration for the neural network.

The reliability of the gradient descent algorithm in higher dimensions is the solution to something called the curse of dimensionality. We spoke to Yoshua Bengio, one of the pioneers of something called deep learning, where neural networks are incredibly complex and have lots of layers, leading to very high dimensional vector spaces to explore to find the best mathematical function to perform a machine learning task.

It had been thought that it would be impossible to optimise things for these bigger neural networks. The fear was that the machine learning algorithms, such as the gradient descent algorithm, would always get stuck in some sub-optimal solution – one of those local minima or pits of despair on the side of the mountain – rather than reach the best possible solution. But in fact Bengio and colleagues were able to mathematically prove that you are more likely to find yourself at a saddle point, rather than a local minimum in these higher dimensions, and in fact machine learning performance gets better with bigger neural networks.

So whether you're lost on a mountainside, or training a neural network, you can rely on the gradient descent algorithm to show you the way.

Read more about machine learning and its many applications on Plus.

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.