
Things don't need to be perfectly round to count as balls. Footballs, golf balls, and tennis balls have seams and dimples, and even the Earth isn't perfectly round because it has mountain ranges and is slightly flattened at the poles. Yet, we still think of all of these things as spherical.
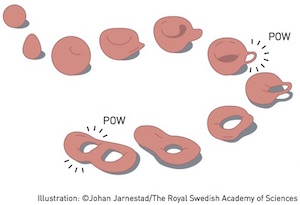
The only way to transform something with no holes (such as the ball in the top left of the image) to something with one or two holes is to tear or puncture the object. This figure first appeared on Plus in the article The shape of things to come.
In mathematics, this tolerance of deformation is captured by the field of topology. Topology considers two objects the same if you can deform one into the other without tearing or cutting: only bending, stretching and squeezing is allowed. The most famous example is that, topologically speaking, a ball is the same as a bowl, and a donut the same as a coffee cup. If a ball or a donut were made out of clay you could bend and stretch them to form a bowl or a coffee cup respectively. But you can't turn a bowl into a coffee cup without tearing or cutting a hole.
This suggests that, when it comes to surfaces such as spheres or donuts, the number of holes is what makes the difference between two objects. And this is indeed correct. Mathematicians have proved that many surfaces that naturally spring to mind are topologically equivalent to either a sphere (with zero holes), the surface of a donut (technically called a torus, which has one hole), or a torus with two holes, three holes, etc. The number of holes is what defines such a surface in the topological sense.

A sphere, a torus, a surface with two holes, and a surface with three holes. Image of sphere: Geek3, used under Creative Commons licence.
By "most surfaces that naturally spring to mind" we mean surfaces that are closed and orientable. Closed just means that the surface has no boundary you could fall off if you were walking around on it (an example of a surface with a boundary is a disc) and that you can paint it with a finite amount of paint (technically, that it is compact). Orientable means, loosely speaking, that there's a clear difference between the two sides of the surface (eg an inside and an outside). That's in contrast to the famous Möbius strip, which only has one side. (See here for more detail on a surface being closed and orientable.)
Coming back to ordinary objects, we now see that a bowl belongs in the zero hole category, a cup into the one hole category, a pair of spectacles (without the glasses) into the two hole category, and a pretzel into the three hole category. In technical terms, the number of holes of a surface is called its genus.
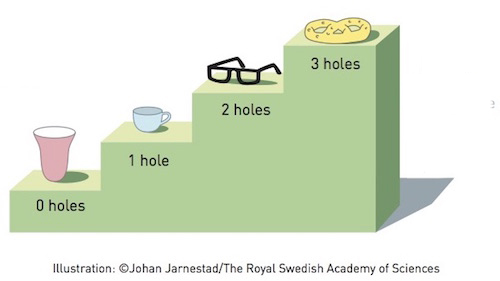
Some objects ranked by their number of holes. This figure first appeared on Plus in the article The shape of things to come.
Surfaces are two-dimensional objects, but mathematicians are also able to think in higher dimensions. A natural question that arises here is how to topologically characterise a three-dimensional sphere (which nobody can properly visualise, so don't worry if you can't). The question proved very difficult to answer. It involves one of the most famous problems in maths — the Poincaré conjecture — a $1,000,000 prize and prestigious medal, and a reclusive mathematician who would accept neither. Find out more in this article.
In higher dimensions, surprisingly, things get a little easier again. The nature of so-called manifolds — analogues of surfaces — is well understood for these dimensions.
This article is based in part on the Plus article The shape of things to come. To find out more about topology you can also read: