
Introducing the Klein bottle
If you like a drink, then a Klein bottle is not a recommended receptacle. It may look vaguely like a bottle, but it doesn't enclose any volume, which means that it can't actually hold any liquid. Whatever you pour "in" will just come back out again.
How do you construct such a strange thing and why would you want to construct it? The mathematician Felix Klein, who discovered the bottle in 1882, described it as a surface that "can be visualised by inverting a piece of a rubber tube and letting it pass through itself so that outside and inside meet".
It's obvious that the Klein bottle, just like the more familiar sphere, is a closed surface: it's finite in the sense that you can fit it into a finite region of space, but an ant could walk around on it forever without ever encountering a boundary or falling over an edge. Unlike the sphere, which has an inside and an outside, the Klein bottle is one-sided: walking around, our ant could reach both sides of each point of the surface. This is why the bottle encloses no volume, and it also answers the "why" question: the Klein bottle is interesting because we don't encounter many one-sided shapes in nature. (See here for another very pretty picture of a Klein bottle.)
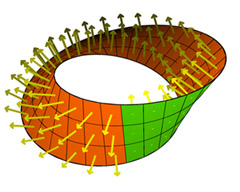
The Möbius strip is one-sided - view the animated version. (Image and animation by Konrad Polthier.)
If this is a bit confusing, think of a simpler example of a one-sided surface: the famous Möbius strip. You can make one by taking two ends of a strip of paper, giving the strip a twist, and then gluing the ends together. By using a strip of paper whose two sides have different colours, say green and orange, it's easy to convince yourself that the resulting Möbius strip is one-sided. Once you have twisted and glued, you'll find that you can reach every orange point from every green point without having to pierce through the paper or climbing over its edge.
Unlike the Klein bottle, the Möbius strip does have a boundary — it is made up of the two non-glued edges of the original strip. But there is a link between the two. If you take two Möbius strips and create a closed shape by joining their boundaries using an ordinary two-sided strip, as shown below, what you get is exactly the Klein bottle.
band whose back and front sides are colored white and blue respectively. Animation by Konrad Polthier.
This fact inspired the mathematician Leo Moser to compose a limerick:
A mathematician named Klein
Thought the Möbius band was divine.
Said he: "If you glue
The edges of two,
You'll get a weird bottle like mine."
Some mathematicians really are multi-talented!
Another curious feature of the Klein bottle is that it intersects itself, which means it's hard to make it from a single tube of rubber as Klein suggested. Strictly speaking, the self-intersecting object depicted above isn't a Klein bottle, but (as Klein indicated) only a visualisation of one. To understand why, first think of the more familiar doughnut (known mathematically as a torus). You can make a torus from a square sheet of rubber by first gluing two opposite sides to form a cylinder, and then gluing the two boundary components of that cylinder to get the torus.

Making a torus: First glue opposite points on two opposite sides of the square to make a cylinder and then glue the two boundery circles of that cylinder (corresponding to gluing opposite points on the remaining two sides of the square) to form a torus.
If you don't want to bother with the gluing, you can simply think of the torus as a square, keeping in mind that opposite points on opposite sides are considered the same. So when you slide a shape drawn on the "square" across the top edge, it will re-appear at the bottom edge and when you slide it over the right edge it will re-appear at the left edge (and vice versa).
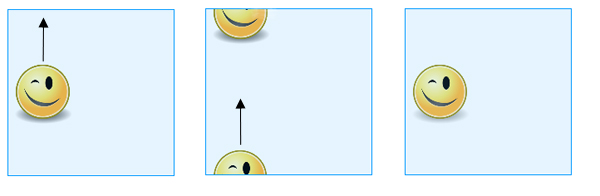
When you slide a shape drawn on the "square" across the top edge, it will re-appear at the bottom edge.
To get a true Klein bottle, start in the same way, identifying opposite points on a pair of opposite sides of a square. For the other pair of sides, however, don't identify points that are directly opposite, but points that are diagonally opposite, as shown in the picture.
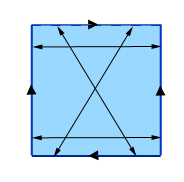
Making a Klein bottle: identify opposite points of two opposite sides (the vertical ones in this picture) and then identify diagonally opposite points on the remaining two sides. (If you label points on the top and bottom sides from left to right by the numbers 0 through 1, then a point with label x on the top side is identified with the point with label 1-x on the bottom side.)
The resulting object is the Klein bottle. Again, you can think of it as a square, keeping in mind which boundary points are considered the same. If you slide a shape over one of the edges that had opposite points identified (vertical in our picture), it reappears reappear on the opposite side, like before. If, however, you slide it over one of the edges whose points were identified diagonally (horizontal in our picture), it appears on the opposite side, but displaced and as a mirror image of its original self.
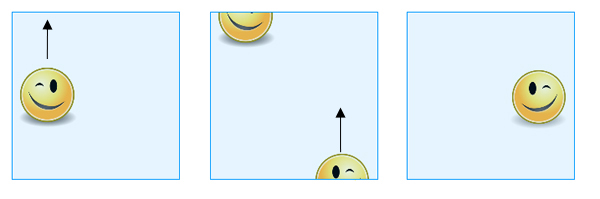
If you slide a shape over the top edge, it appears across the bottom edge, but over to the other side and as a mirror image of its original self.
The only way to build this shape in three-dimensional space by actually gluing points together is to allow it to intersect itself. This amounts to identifying pairs of points in the interior of the original square, so strictly speaking the resulting shape is not exactly the same as the Klein bottle, which only has boundary points identified. It's just one way of representing the bottle in three-dimensional space (there are others too).
Mirror image and orientability. Animation by Konrad Polthier.
Curiously, the concepts of "inside", "outside" and "one-sidedness" depend on the ambient space an object is sitting in. For example, a loop drawn on a piece of paper (in two-dimensional space) has a well defined inside and outside, but a loop drawn in three-dimensional space doesn't. This is why we can't talk about one-sidedness unless we first decide how to embed a surface in three-dimensional space. There is, however, a closely related property that is intrinsic to a shape and doesn't depend on the surrounding space. A surface is called orientable if you cannot slide a shape drawn on it around and back to where it started so that it looks like its own mirror image. As you can see in the animation accompanying the image on the right, the Möbius strip isn't orientable. And as you can see from the image with the smiley face above above, neither is the Klein bottle. To give it its full mathematical description, the Klein bottle is a closed, non-orientable surface. To find out more about it see the article Inside the Klein bottle.
About the author
Marianne Freiberger is Editor of Plus.
Comments
Anonymous
Surely the Klein bottle has volume. If you pour in the liquid at the top opening through the green inside of the tube the liquid will fill up the tube until it reaches the point where the green inside becomes the white outside and then it will be full. How do you think the liquid will just come back out again?
Anonymous
exactly
Anonymous
This would not be true as it is in 4d.
Klaws
A proper container has two surfaces, one keeping the outside out and one keeping the inside in.
Just like the Moebius Strip, the Klein Bottle only has one surface. If that's the outer surface, then yes, you can pour water into the outside (#1). Or if it's the inner surface, than you can pour water inside (#2). Haha, no, you can't as the water was already on the outside (#1) or on the inside (#2).
You can arbitrarily defines any part of the surface as "inside" or "outside", but this doesn't make sense topologically. It's like taking a chessboard and saying "I call the black squares are 'inside', and the white ones 'outside'."
And yes, you can pour water on a chessboard. Smash the back squares with a mallet first, and they might actually hold water.
What we see when we see a "real-life Moebius Strip" or a "real-life Klein Bottle" are actually imperfect illustrations (and, in case of the Klein Bottle, additionally a 3D projection of a 4D object). Topologically, the strip should have zero thickness, and the bottle walls the same.
Fun experiment: what's the "inside volume" of a bowl? (You can measure it by weighing the mass of water it holds at 4°C, one liter will be 1kg). Now turn it upside down. Has it still the same "inside volume"?
Correct answer for the bowl: it's not how much water it can hold, it's how much water it displaces when it gets fully submerged. That's for a real-life bowl. A theoretical topological bowl doesn't have any volume.
Anonymous
Being exact, a "standard" bottle encloses a volumne only if you put a cover on it.
The same applies to the Klein bottle. If you cover it at the "green end" (see aboves video) you will be able to distinguish "inside the bottle" and "outside the bottle" and thus the Klein bottle encloses a volumne in the same sense a "standard" bottle encloses a volumne.
Anonymous
Please see http://vimeo.com/20390916
But then it's not the bottle because it's always on the outside or what?
Anonymous
us humans cannot make a true klein bottle as we only have a presence in three dimensions whereas a true klein bottle would have to be four dimensional.
Anonymous
Animation of two sided sheet runs for 12 seconds. Stop animation at 5 second point. It becomes very apparent that the Klein bottle has an inside and outside but only 1 surface. A Mobius surface?
Liquid is held in by the funnel inlet and the fat "bottom". Seal for filling is the penetration of the funnel neck into the fat bottom. A single surface having volume and inlet/outlet opening...Amazing.
Frank
To "fill space" in this mathematical context it means to "displace". When submerged in water the water level wouldn't rise. Unless of course the klein bottle had water in it prior to being submerged.
Anonymouse
If you saw the animation above, you saw how it started as a simple sheet of paper, that was folded into a simple cylinder. Then, that cylinder became curved and at a rather odd angle. It then turned a full 90 Degrees, and the bottom tip of the cylinder expanded into a funnel-like shape. It then overlapped the top section of the shape, causing it to seem like the cylinder went through the funnel that it was connected to. The funnel then began to expand and rise, while the top part of the cylinder's "edges" curved and began lowering until it met up with the funnel. If you poured water into the hole, it would simply run through the mid-section of the cylinder, then it would (if the water pressure was high enough) rise to the funnel, filling the funnel and the whole shape completely (The Water inside the funnel part would be surrounding the cylinder, and NOT rising out of the whole.) Those videos you see about people filling Klein Bottles: FAKE. Even if 4D did exist, the Klein Bottles they use aren't actually Klein Bottles. The ones they use are actually built far differently than the model shown above, or in other words, they are not the real Klein Bottle. This is how the Klein Bottle really does have volume.
#11 year old
Anonymous
its 4d and cannot have a volume because it only has one side and im sure that you know you can pour water on anything one-sided and it doesnt "contain" water very well. the tube that enters the klein bottle and "clips" through the side of the bottle doesnt actually enter that way, the edge of the bottle is never breached, it enters through the fourth dimension.