Last month David Thouless, Duncan Haldane and Michael Kosterlitz were awarded the 2016 Nobel Prize in Physics for their work using mathematical methods from topology to understand strange phenomena in materials.

Topology in action

Topology is the area of maths that describes the properties of objects that remain unchanged (called invariant properties) when you are allowed to bend, stretch or squash the object, but not cut or tear it. The most famous example is that, topologically speaking, a ball is the same as a bowl, and a donut the same as a coffee cup. If a ball or a donut was made out of clay you could bend and stretch it to form a bowl or a coffee cup respectively. But you can't turn a bowl into a coffee cup without tearing or cutting a hole.

Thouless, Haldane and Kosterlitz haven't been recognised for their ability to squash or stretch physical materials. Instead they used the topology of the states of the quantum particles involved to understand surprising observations and predict strange new states of matter.

The hole truth of topology

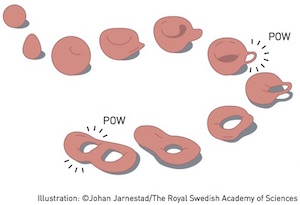
The only way to transform something with no holes (such as the ball in the top left of the image) to something with one or two holes is to tear or puncture the object.

The example of the bowl and the coffee cup illustrates a topological invariant called the genus of these shapes: that is, the number of holes they have. A bowl has no holes (genus 0), a coffee cup has one (through the handle – making it genus 1), a pair of spectacles (without the pieces of glass) has two holes (genus 2), and a pretzel can have three holes (genus 3). The genus of a shape always remains unchanged in topology as the only way you can change the number of holes is by tearing or gluing the shape, which is of course against the rules.

Another important concept in topology is the winding number. In two dimensions, this refers to how many different ways you can wrap one circle around another. You can picture it as winding a rubber band around your finger. If it just circles your finger, untwisted, it's wound its way around once and we say it has a winding number of 1. If you loop it round twice, it has a winding number of two, three times and it has a winding number of three and so on. A winding number of 0 is when the rubber band isn't on your finger at all. And all of these windings, with different winding numbers, are topologically distinct: you can't change a rubber band wound around your finger twice, to one that is wound once, without lifting a loop off your finger, which is equivalent to cutting the band and regluing it.

You can extend the idea of winding numbers to higher dimensions, say wrapping a circle around a sphere. There's only one way to do this – any rubber band on a sphere will just slide off giving a winding number of 0. This is quite a different situation to wrapping a circle around donut, which can be done in infintely many different ways. For example your rubber band could encircle the donut, passing through the hole once, twice or more times. You can even think about wrapping a sphere around another sphere, or indeed move into even higher dimensions. (You can read a more detailed introduction to winding numbers in this article, and there is an excellent introduction to extending the definition to higher dimensions in this presentation by Mark Behrens. You can also read more about how these ideas can be used in this article on the fundamental group.)

The surface of a doughnut is not the same as a ball. There is only one type of closed curve on the surface of a ball, whereas there are many different closed curves on the surface of a doughnut, including the three shown here.

Topological invariants, like the genus (the number of holes in a shape) and winding numbers, have an interesting feature: they only ever take whole number (integer) values. And this step-wise nature of these topological concepts allowed Thouless, Kosterliz and Haldane to explain surprising phenomena observed in experiments and to predict new types of materials.

Quantum hall effect

Thouless was awarded this years Nobel Prize in Physics in part for his work explaining the quantum Hall effect – a strange phenomenon that was only recently discovered but has a long history. In 1879 Edwin Hall discovered that if you restrict some electrons to move in a flat plane (eg, by using a very thin sheet of material), turn on a magnetic field perpendicular to the sheet, and run a constant current along one direction of the sheet, then a voltage V_H (called the Hall voltage) is produced in the opposite direction along the sheet. The Hall voltage would be zero without the presence of the magnetic field. But switch the magnetic field on and the Hall voltage increases in-line with any increase in the strength of the magnetic field.

In 1980 Klaus von Klitzing discovered a striking change in this effect that occurs when you run the experiment at very low temperatures. He studied a thin layer of electrons sandwiched flat between two semi-conductors, cooled to about a degree above absolute zero and subjected to a strong magnetic field applied perpendicular to the layer. When a current ran through the layer in one direction, a Hall voltage was produced in the opposite direction. But, very surprisingly, the Hall voltage didn't vary in-line with an increase of the magnetic field. Instead, the voltage was quantised: it only took on precise integer values. As Klitzing increased the strength of the magnetic field, the Hall voltage would stick at one value for a while until it would suddenly jump to the next integer value.

This was a great surprise. Such quantised behaviour is familiar at the very small scales of quantum mechanics which comes to the fore at very low temperatures. But Klitzing observed this quantisation in the macroscopic properties of conductance and voltage that emerge in a much larger system involving many particles.

Taking the next step with topology

This striking behaviour could not be explained using the physics of electrical conductors known at the time. In 1928 Felix Bloch had solved an equation which gives a description (called the wave function) of the quantum behaviour of electrons in a solid, revealing that the wave functions of electrons form discrete energy bands. This led to our understanding of how materials conduct electricity. The lower energy bands are filled in an insulator with a large gap to the next band: insulators do not conduct electricity as there is nowhere for the electrons to easily flow. While in a conductor, these bands are only partially filled allowing electrons to flow through the system. The conductance of a material (the ability of the system to conduct electricity, used to calculate the voltage) is described using something called the Kubo forumula, based on the structure of these energy bands.

Thouless realised that the topology of shapes corresponding to the wave functions of the electrons in the energy bands had a part to play in understanding conductance. If the winding number of the wave function was 0, the topology was trivial, like that of a sphere or flat plane. In this case there is no Hall conductivity: if you apply an electric field, current will only flow parallel to the field. But for the more complicated topologies that arise at low temperatures, the Kubo formula links the integer-valued winding numbers of the wave functions to the conductance: giving the step-wise change in the conductance and Hall voltage seen in the quantum Hall effect.

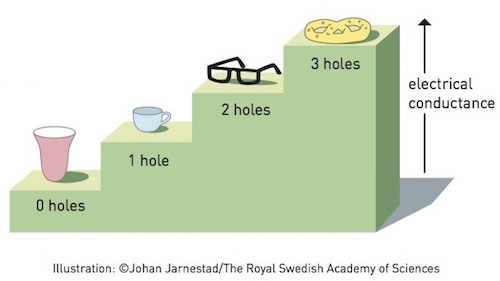
The topology of the wave functions of the electrons in the energy bands gives the step-wise change in the conductance.

The thin layer of material in Thouless' model is now known as a topological quantum fluid. This topological nature only arises from the behaviour of the whole system of electrons, and can't be ascertained by looking at the behaviour of individual electrons in the system. This mirrors the topological invariants such as genus and winding numbers which can only be determined by looking at the whole shape, rather than just a small section.

In 1988 Haldane, theoretically predicted that topological quantum fluids, like the one seen in the quantum Hall effect, can form in the layer between semiconductors, but without the presence of a magnetic field. He said he never dreamed of his theoretical prediction being produced in reality, but it was finally experimentally observed in 2014.

You can find about the other ways topology won the Thouless, Haldane and Kosterlitz the Nobel prize in the next article...

About this article

Fiona Burnell

Rachel Thomas is Editor of Plus. She would like to thank Fiona Burnell, a mathematical physicist at the University of Minnesota, for patiently explaining the science and mathematics behind this year's Nobel Prize. She interviewed Burnell in October 2016, and also in July 2013 for the booklet, Mathematical physics: what is it and why do we need it? produced for the Institute of Physics.