
In space, do all roads lead to home?

Figure 1: Getting nowhere
Imagine you walk down a strange street and pass a gate in a wall. You keep walking in a straight line only to pass another gate in a wall. You keep walking and pass yet another gate, yet another wall. You might begin to suspect it is the same gate, the same wall. Even though you walk in as straight a line as possible, never turning back, you come upon the two landmarks again and again.
This, of course, could actually happen on the surface of the Earth, on a much larger scale. If you started in London and walked in as straight a line as possible for a very long time, you would eventually come back to London. This is because the Earth is curved and finite, and has a surface with the overall geometry of a sphere.
Over the past few hundred years we have made ourselves quite familiar with the Earth's compact surface, charting oceans and flying around the globe. Here I'm using the word "compact" to mean that the surface has no edge, but rather is smoothly connected to itself. With this definition, the surface of a sphere is compact, and so is the surface of a bubble or a doughnut. The surface of a square would not be compact, because it has edges. However, a compact surface can be made from a square by smoothly gluing the edges of the square together as we do below.
A remarkable possibility is that the entire universe is compact and connected. In other words, if we were to launch a spaceship from Earth and fly in as straight a line as possible, we could find ourselves returning home. As we see the Earth receding in the distance behind us, we might also see it growing nearer in front of us.
A compact universe is far more dramatic than a compact planet. From Einstein we have learned that the universe has three spatial dimensions and one time dimension. According to his theory of relativity, we all move along the natural curves in that space. Even light follows these curves.
If that strange street lived in a short, compact universe, the world would get even stranger. Light from the street lamps would wrap around the compact space, following the natural curves. If you were to stand there you would see ahead of you the light reflected off the street which had traveled all the way around the space.
Further in the distance, you could see the same scene again: yourself standing in the middle of the more distant but otherwise identical copy of the street. Like a hall of mirrors, the pattern would go on infinitely and in all directions. Though we know from personal experience that the universe is not this small, it could be finite and compact on a much huger scale: thousands of times the size of a galaxy, but finite nonetheless.
To visualize how this is possible we can can utilize the geometry of surfaces. The geometry of surfaces can be classified according to two properties, the local curvature of the surface and the global topology of the surface.
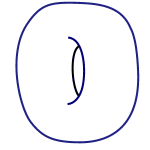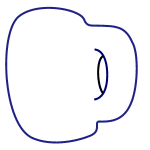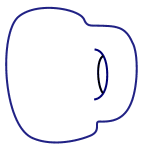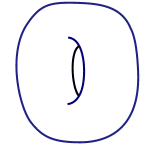
Figure 2: A doughnut mug
Topology is the branch of mathematics that describes properties which remain unchanged under smooth deformations. If we imagine surfaces to be made of clay, a smooth deformation is any bending, mushing and shaping which does not require the discontinuous action of a tear or a punching of holes. A favorite example is a clay doughnut which can be smoothly manipulated into the shape of a coffee
mug. The doughnut hole becomes the coffee cup handle so that the number of holes is preserved. The doughnut and the coffee mug therefore have the same topology.

Figure 3: square to cylinder
We can make topologically connected surfaces with handles and holes by starting with a flat rectangular sheet of paper. You can glue the left edge to the right edge to make a cylinder:
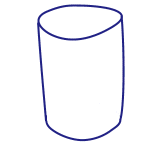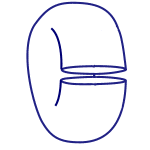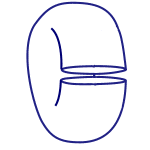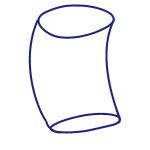
Figure 4: cylinder to torus
If you then glue the top to the bottom, you would have a torus, the topological equivalent to the doughnut and the coffee cup:

Figure 5: A Möbius strip
If you glued the left to the right after twisting the sheet of paper by 180 degrees, you would build a Möbius strip. If you walked around the Möbius strip starting on one side, you would find yourself on the other side after one full trip and on the starting side again only after two full trips. This property is known as non-orientability.

Figure 6: A Klein bottle
Gluing the top of the Möbius band to the bottom would give you a compact Klein bottle, a complicated shape that is impossible to draw properly in three dimensions. These four surfaces are the only connected surfaces that can be constructed from a flat rectangle.
Notice that we started with a flat sheet of paper and then built a torus. However, the torus we drew in figure 4 is not flat. It is curved in a way that is not constant across its surface. This is an artifact of living in 3-dimensions and bending the 2-dimensional sheet of paper into 3 to help our 3-dimensional selves visualize the compactness and topology of the surface.
Strictly speaking, a two-dimensional flat space can exist which has the fundamental shape of a rectangle with its edges glued together in pairs, but which doesn't bend up into three dimensions.
This truly flat torus has the same topology as the torus we built of paper. However, it is not curved and does not even require the existence of three dimensions. A video game works this way, as does the strange recurrent street above. Old-fashioned cartoons worked like this too. If you've ever seen the Flintstone you've seen Fred running through his house and passing
the same window and lamp over and over again.

Figure 7: Space to bee in
We can get rid of the third dimension entirely and visualize a compact surface using a tiling picture. Consider flat creatures living on a flat torus that has the fundamental shape of a rectangle. A flat explorer can mark their starting point and then walk straight from left to right. After traveling a distance L, they will come back to where they started.
We can represent this within one fundamental cell by following simple rules each time we cross an edge.
If we exit the right edge, we reenter the left edge.
If we exit the top, we reenter the bottom edge and so on.
Figure 8: Lots of space to bee in?
Alternatively, we can visualize the the compact space by gluing together identical copies of the fundamental cell edge-to-edge according to our simple rules. We take an identical copy of the original tile and glue the left edge of the copy to right edge of the original. We then glue the lower edge of another copy to the top of the original and so on until all the edges of the original are tiled against copies.
We then take more identical tiles and glue them to the edges of the copies. We follow these rules until the entire infinite plane is tiled.

Figure 9: Home at last
We could have started with a hexagonal flat cell instead of a rectangular cell. The edges of the hexagon can also be glued together in pairs to make another torus, so the fully identified hexagon has the same topology as the fully identified rectangle. We can also represent the flat hexagonal torus as a tiling of flat space, as in fig. 9.
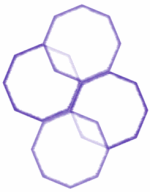
Figure 10: Don't buy octagonal tiles for your bathroom!
We could try to tile flat space with other single fundamental cells, but we would find our efforts thwarted. (Remember, we're talking about really identical tiles - no rotations allowed, so triangles won't do!) For example, try to tile a flat surface with an octagon. You'll find that the interior angle of a regular octagon is 135 degrees. If we try to glue octagons together around a vertex, two would leave a gap and there wouldn't be enough room for three.
At the end of the day, only hexagons and rectangles (or, more accurately, parallelograms) can tile a flat plane. It is for this reason that many bathrooms, metro stations and the like are tiled in hexagons and squares.
The octagon cannot tile a flat plane, but it can tile a surface which is everywhere negatively curved. Such a surface cannot be drawn in three dimensions, but it can be imagined as a surface which everywhere has the curvature of a saddle.
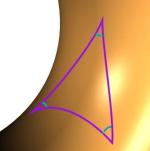
Figure 11: A surface with negative curvature
While the interior angles of a triangle add up to 180 degrees in flat space, the angles sum up to less than 180 when drawn on a negatively curved space, and more than 180 when drawn on a positively curved space. For this reason, if we draw the octagon just the right size on a negatively curved space, we can fit just the right number snugly around a vertex and fully tile what is known as the
hyperbolic plane.

Figure 12: A double torus
We can go ahead and bend the octagon into three dimensions to get an idea of the topology generated by this tiling of the hyperbolic plane. By gluing opposite sides of the octagonal cell we can build the double torus of fig. 12. The double torus can be deformed into a mug with two handles. It therefore has a different topology from the torus of fig. 4, which was be deformed into a mug with only one handle.
These two-dimensional examples give us an idea of how to build the more difficult three-dimensional, topologically compact spaces. We cannot visualize these as bent into four spatial dimensions since we only have three at our disposal. But we can begin first with a volume of fixed curvature, select a fundamental tile, and apply the rules for gluing the edges.

Figure 13: Gluing cubes
For instance, we can begin with a flat 3-dimensional space and select a cube as the fundamental cell. We can then glue the faces of that cell in pairs and use those gluing rules to lay down these three-D cells to fill the 3-volume with identical cubes.
Our own universe may be such a vast cube and cosmologists and mathematicians have pooled their efforts over the past few years to try to observe the global topology of the cosmos. The observations rely on an imprint of the geometry in intricate patterns in the sky and we await the data from future satellite missions to answer our questions.
Even if the universe is compact, it may well be too huge for us to see all the way around. In the meantime, we can't be sure if those are all new galaxies on the horizon, or if it really is ourselves we see at the observable edge of the universe.
About the author

Janna Levin received her PhD from M.I.T. in Theoretical Physics/Astrophysics. She has worked at various international centers including the Center for Particle Astrophysics in Berkeley, California, the Canadian Institute for Theoretical Astrophysics in Toronto and the Astronomy Centre at the University of Sussex. She is currently an Advanced Fellow in the Department of Applied Mathematics and Theoretical Physics at Cambridge University.
Comments
Anonymous
Dr. Levin,
I just read your explanation of a compact universe and found it to be just the applied topology example I was looking for. Thank you very much for dedicating some of your time to making such understandable science.
Regards,
Ariel Martinez Salas
Anonymous
Perhaps your explanation makes sense to those familiar with the jargon, but otherwise it leaves much to be desired. For example, 'gluing' edges or faces together is difficult enough to visualize without being more specific; and how does fig. 11 represent a 'double torus' formed by gluing opposite sides of an octagonal cell together? Please. You're going to need to be more descriptive.
Rachel
You are quite correct, the text should have referred to figure 12 as representing a double torus. We've correct that mistake.
As someone who doesn't think visually myself, I agree that the concepts can be quite difficult to visualise. In the past I've ended up making some of the simpler shapes with material and a stapler which then helped me believe some of the more complicated constructions. (No paper and glue for me: material is more bendy than paper and glue... I have no patience with glue!) In particular I think I ended up attempting a double torus using stretchy material. I must admit it didn't really work but it did help me to visualise it in an ideal setting; that after sticking together two pairs of opposing edges, there were still two other pairs of edges to stick together to make two, joined, tori.
The other thing that might help is the Plus article Imaging maths – Inside the Klein bottle. The animations and cut-away views allow you to explore the surfaces which certainly helped me to visualise these shapes.
Anonymous
You did a great job. It help me to understand compact universe and its impact more clearly.
Faheem (Pak)
Anonymous
> only hexagons and rectangles (or, more accurately, parallelograms) can tile a flat plane.
That's not true. There are a lot of pentagons that can do the same thing (google Marjorie Rice for details). Also, there are more quadrangles that also can tile a plane.
Anonymous
"A remarkable possibility is that the entire universe is compact and connected. In other words, if we were to launch a spaceship from Earth and fly in as straight a line as possible, we could find ourselves returning home. As we see the Earth receding in the distance behind us, we might also see it growing nearer in front of us."
"Even if the universe is compact, it may well be too huge for us to see all the way around. In the meantime, we can't be sure if those are all new galaxies on the horizon, or if it really is ourselves we see at the observable edge of the universe."
I am just a regular guy so people never listen to what I say. But I have been making both of these points for years. On the surface, they just seem logical. I think the galaxies are traveling in circles, but the circle is so huge that we think it is a straight line. And it takes so long to get back to where you started that you may never get back. But new galaxies come into being and continue the journey.
Anonymous
Not so much logical as intuitively romantic.
Anonymous
Great Article
Souparna Nath
Quite an impressive review!
Just 2 small correction -
1) There is another compact surface besides the 4 you have mentioned that can be constructed from a flat 2D square. Its constructed by gluing each pair of opposite edges with a 180 degree twist. It's called "Boy's Surface".
2) A 2D Torus T^2 has a only Extrinsic Curvature, but NO Intrinsic Curvature.
Ruwan Rajapakse
Dear Professor
You have explained compact surfaces. But how does this get tie up with general theory of relativity or it's derivative Friedman equation. Or any other physical theory.
There has to be another paper.
1. Let us take a look at Friedman equation. It has the Hubble constant and cosmological constant. Both are non zero entities. How would the compact topology work with this situation. Also einstein's field equations describes a dynamic universe, even without the cosmological constant. The universe was born this way.
Did the universe born with a compact topology just after the big bang?
2. Raycahudhuri equation suggests that all geodesics will come together and form a singularity in the future if there is no cosmological constant. Since the existence of cosmological constant is proven from super nova observations the universe is expanding and also accelerating.
My question is how would the compact topology works out with accelerating universe.
3. My third question is whether there is any theory that connects particle physics with compact topology?