
Why we need a mathematics of movement
Brief summary
The same types of mathematical model can be used to describe the movement of all kinds of organisms, from cells to humans. This allows for rich cross-fertilisation between cell biology and animal ecology. Areas such as cancer research and the conservation of endangered species all stand to benefit.
There are several types of cancer which spread through the collective movement of individual cells. Scientists believe that in many of these cases there are leader cells who guide the direction and follower cells that follow along, but the exact mechanisms behind the communal movement are still mysterious.
If the follower-leader model is true, then here's a thought: could we create artificial leader cells, tiny robots that we can control, and use them to lead follower cancer cells into directions that cause the least damage? Scientists have begun exploring this idea, inspired by the fact that you can fool certain types of bird or fish into following a robotic leader. It could also work in other situations where collective cell movement occurs, for example in the normal development of organisms. Here cells could be lead in the correct directions to avert developmental defects.
The idea is based on an interesting observation. When it comes to movement, all types of organisms, whether they have a brain or not, are trying to accomplish similar things using the same methods. They are striving towards some goal — find nutrients, stay close to mates, or escape danger, for example — and they do so by reacting to cues from their environment.
"You would think that animal movement would be very different to cell movement because animals think, but both are trying to accomplish the same things and they use the same mechanisms," says Philip Maini, a mathematical biologist at the University of Oxford and co-organiser of a research programme on the Mathematics of Movement (MMV) which was held at the Isaac Newton Institute for Mathematical Sciences (INI) last year. "And although we humans are higher organisms who can think, in many ways we haven't been able to out-think cells that have no brain."
For a spectacular example, look at the video below. It shows a network formed by a slime mould called physarum polycephalum: scientists placed an initial slime mould culture on a map of the surroundings of Tokyo, at the location of the main city. They then placed the slime mould's favourite food (rolled oats) on the locations of other cities surrounding Tokyo. The network the slime mould developed to get to the oats and transport the nutrients resembles the human made railway network which connects these cities. Indeed, there have been suggestions that the slime mould is better than we are at solving the travelling salesperson problem, which humans find extremely hard. The scientists behind this experiment, which included colleagues of Maini's at the University of Oxford, received a 2010 Ig Nobel Prize for their work (you can read more in their paper published in Science).
Generally, the study of movement can provide deep insights into all sorts of processes. "To understand how something works, the basic approach is to understand how it moves," says Guillermo Abramson of the Instituto Balseiro; Centro Atomico Bariloche, who co-organised the MMV programme.
When you try to understand and describe movement you quickly find yourself using the language of mathematics. This is what happened to Isaac Newton, who in the 17th century formulated his famous laws of motion using mathematical equations. These laws work amazingly well for inanimate objects that move under the influence of a force, such as the planets in our solar system.
When it comes to living things, however, Newton's laws lack a crucial element. Perhaps surprisingly, this element has nothing to do with the secret of life, or the mystery of consciousness. What Newton's laws are lacking is randomness. This enters the picture, not only because living things can be capricious, but also because no organism can sense its environment with 100% accuracy. Whether it's a lion following the scent of prey, or a human struggling with Google maps, the lack of precision leaves room for random wriggles in the path towards their goal.
"There is lots of information uncertainty in the environment, and the way an organism moves around has to do with that uncertainty, so there is always some randomness," says Luca Giuggioli, a complexity scientist at the University of Bristol and co-organiser of the MMV programme. "That happens for cells, and also for larger animals. After Newton people started to wonder about what happens when there is uncertainty and how to describe it, and that created a whole new area of mathematics describing movement."
Drunken walking
An important concept in the maths of movement is what mathematicians call a random walk or a drunkard's walk. You can generate one quite easily by placing yourself in the middle of your garden or local park. Pick a random direction and walk one step in that direction. Then pick another direction at random and walk one step in that direction. And so on. The result, traced on a map, will look something like this:
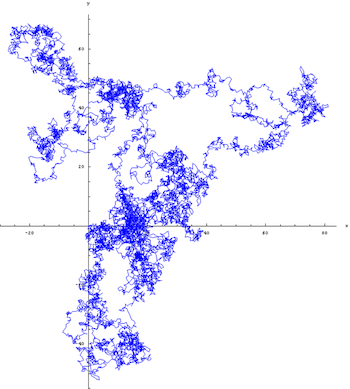 10,000 steps of a random walk generated on a computer. Image: Zweistein~commonswiki, CC BY-SA 3.0 DEED.
10,000 steps of a random walk generated on a computer. Image: Zweistein~commonswiki, CC BY-SA 3.0 DEED.
Similar random motion occurs in nature, for example with particles suspended in a liquid or gas. This was first observed in 1827 by the botanist Robert Brown, while looking through a microscope at pollen immersed in water. It's therefore called Brownian motion. The process described above, transposed into three dimensions and phrased in the language of maths, gives a mathematical model of Brownian motion.
Living things tend to move with more purpose than pollen, of course, but a tweak to the rules above can produce a more realistic result. Imagine that at each stage you don't only choose the direction at random, but also the distance you travel into that direction (so it's not just one step). However, you rig your random number generator in such a way that short distances are more likely to be picked than longer ones (to be precise, you rig it in such a way that the distances follow a power law distribution).
The paths that result from these rules look like Brownian motion interspersed with long distances travelled in one direction only. That's because, even though long distances are less likely to be picked than shorter ones, they are still likely enough to get picked occasionally.
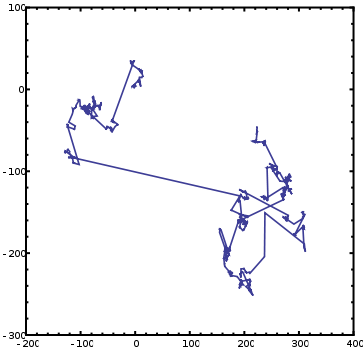 1,000 steps of a Lévy walks generated on a computer.
1,000 steps of a Lévy walks generated on a computer.
These kinds of random walks are called Lévy walks, and are similar to what you see when you let your dog off the lead in a park. It'll sniff out a small patch, then dash off in a random direction to sniff out another patch, and so on. Indeed, a seminal paper published in 1999 suggested that Lévy walks (with a power law exponent of 2) provide the best strategy for searching for things that are sparsely distributed in space, like interesting tidbits a dog might be looking for in a park. The suggestion is that dogs, as well as many other animals that have been observed to move in this way, have evolved this behaviour as an optimal foraging strategy, although the theory remains controversial.
Adding purpose to randomness
The general idea behind random walks can be used to understand the movement of all sorts of organisms, even those that move with more purpose than a dog in a park. An example comes from the work of Stuart Johnston of the University of Melbourne, who took part in a workshop of the MMV programme. Johnston is interested in the annual migration of whales, in particular, in how the noise that humans cause in the oceans, through shipping and drilling, might impact the whales' ability to find their way.
.jpg)
Minke whales are one of the species Stuart has considered in his work. Image: Anne Smrcina/NOAA.
When whales set out on their long-distance journey each year, they mostly follow two types of signal. One is the calls from other whales, which they can hear underwater over very long distances, and the other we don't quite understand yet — it might be the Earth's magnetic field, or perhaps the sound of icebergs crashing together in the distance. Suffice to say that there is some signal that makes them want to head in a particular direction.
A more sophisticated version of the drunkard's walk can be used to simulate the whales' movement. "Of course we know that whales aren't drunk, so instead of picking a direction at random, we say they pick a direction that's close to where they want to go, but there's still a little bit of randomness; a little bit of uncertainty," explains Johnston. The amount of randomness depends on how well the whales can pick up the two signals mentioned above. The better they can detect them, the less randomness there is, and the quicker they get to their destination.
Using this idea Johnston and his colleagues have built a mathematical model for the collective movement of whales. The model allows you to simulate this movement on a computer and see how it might change if external conditions change. It's still a work in progress, but if the model suggests the noise is too much for the whales, then we can also use it to figure out what we could do to mitigate the damage. You can find out more in our podcast episode featuring Johnston.
Big and small
Not all models of animal movement are based on the concept of a random walk. Our article The dynamics of crowds, for example, describes a model for the behaviour of human pedestrians, useful in the design of buildings or evacuation procedures. This model assumes, Newton style, that people are drawn to move in particular directions by forces. Randomness is still there though, added in through fluctuation terms to make the model realistic.
What's important here is that none of these models rely on the fact that the animals involved are intelligent. They are all about reactions to external cues, and this is something that brainless organisms, such as cells, can also do. Many approaches to understanding larger animals can therefore also be used in cell biology.
This cross fertilisation between animal ecology and the science of small things also works the other way around. An example comes from the mathematician Alan Turing, famous for his WWII work as a code breaker. In 1952 Turing suggested a mechanism for the formation of patterns, such as spots and stripes, in animal skins and coats. It has two chemicals diffusing (randomly) through an animal's skin and reacting with each other, a process that can quite easily be described mathematically. You can find out more in How the leopard got its spots.

The patterning on this cheetah can be explained using Turing's model.
The same idea has been used to model all sorts of other things too, including the flocking behaviour of birds and how it's related to how the birds make use of the space they live in. In this case, instead of chemicals diffusing and reacting, you have birds moving about and responding to each other, as well as their environment.
The aim of the MMV programme was to nurture and extend the connection between cell biology and animal ecology. "Over time both research communities have become very specialised in their mathematical modelling, and yet at the same time we are looking at very similar if not identical structures and quantities to represent movement," says Giuggioli. "We have developed methodologies without actually talking to each other. This is why during the programme there were lots of exchanges about methodologies to look at similar processes, but also at very different ones to exploit each other's expertise."
Now is a good time to foster this kind of research. "There is a whole body of technology to gather the data, both for ecological problems and for cell problems," says Abramson. By this he means technology for tracking organisms — an interesting example is the deep worm tracker, which uses deep learning to track the movements of a particular type of worm. "There's been an explosion of tracking data, it's a tracking revolution, so we need even more sophisticated mathematical tools to represent and analyse movement," says Giuggioli.
Tracking cells within our bodies is usually harder than tracking a larger animal, so in this case it's the cell biology community which stands to learn from animal ecology. "Tracking technology isn't as advanced in cell biology as it is in animal ecology," says Maini. "But when we start getting similar volumes of data, we will know to contact animal ecologists we have met in the MMV programme. It's good to know there's another community, in supposedly a very different field, that has relevant expertise. There's no need to reinvent the wheel."
It's during the MMV programme that the idea of fooling cancer cells into following a robotic leader originated, and scientists are now seeing where it could lead. While cell biology aims to understand the insides of animals' bodies, animal ecology looks to understand their interaction with their environment. In both cases protection, be it from disease or extinction, is a major motivation. There are many benefits to be gained from the unifying framework of the mathematics of movement. For us, and also for the creatures we share the planet with.
About this article
The research programme Mathematics of movement: an interdisciplinary approach to mutual challenges in animal ecology and cell biology took place at the Isaac Newton Institute for Mathematical Sciences in 2023 and was organised by Guillermo Abramson, Helen Byrne, Luca Giuggioli, Paul Kulesa, Philip Maini, and Ran Nathan. You can see other content relevant to the programme here.

Guillermo Abramson is Principal Investigator of CONICET and Professor at Instituto Balseiro (Argentina). His professional activity centres in the study of Complex Systems, in particular the mathematical study of ecological systems.

Luca Giuggioli is Professor of Complexity Sciences at the University of Bristol and his research focuses on developing theoretical models of movement and interaction and to apply them to biological organisms, and animal ecology in particular.

Philip Maini is Professor of Mathematical Biology, and Director of the Wolfson Centre of Mathematical Biology at the Uuiversity of Oxford. His research uses mathematical modelling to generate mechanistic understanding of processes in developmental biology, wound healing and cancer.
Marianne Freiberger, Editor of Plus, interviewed Guillermo Abramson, Luca Giuggioli, and Philip Maini in December 2023, and spoke to Stuart Johnston in September 2023
This article forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
