
Country road, take me home
Sixty-three year-old Avraham Trakhtman has solved one of the current generation's toughest mathematical problems — the 38 year-old road colouring problem. The solution will shortly be published in the Israel Journal of Mathematics.
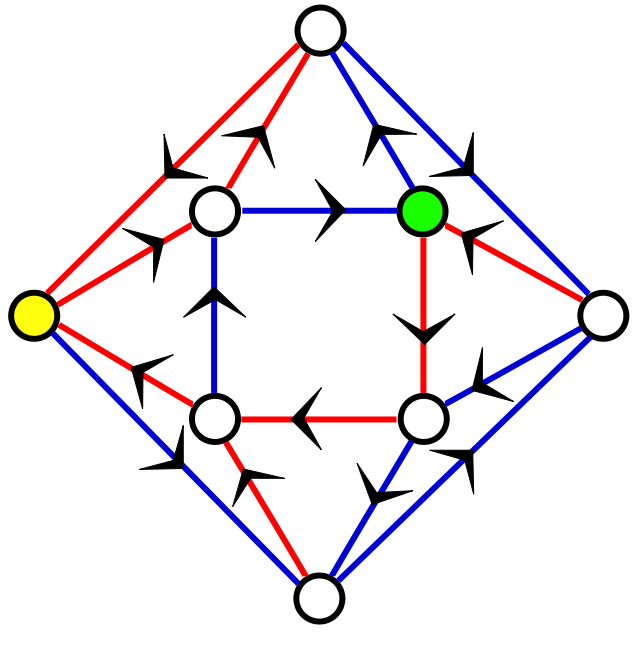
The road colouring problem — no matter where you start, if you follow the instructions blue-red-red — blue-red-red — blue-red-red, you will finish at the yellow vertex.
The road colouring problem, which was first raised by Israeli mathematician Binyamin Weiss in 1970, is a problem concerning synchronised instructions and is expressed simply with the following example:
A man reaches a town he has never visited and drives around trying to find his friend's house. Despite the fact that there are no street names, his friend says not to worry and that he will provide instructions (turn left, then right, then left ...) on how to get there. The road colouring problem postulates that no matter where the man starts his journey (that is, no matter which part of the town he encounters first — he could have approached from perhaps the North or the South) there is a set of instructions that will lead him to his friend's house.
Another version of the problem considers a lost e-mail somewhere on the Internet. The sender wants to make sure it is delivered to the right place, no matter where it already is. The figure to the right shows an example using colours. No matter where you start, if you follow the instructions blue-red-red — blue-red-red — blue-red-red, you will finish at the yellow vertex. The conjecture postulates that it is possible to find such instructions for all such closed systems in which no roads lead out of the system.
The problem is similar to the currently unproven Four Colour Theorem which states that you only need four colours to colour each political region on a map such that two areas sharing a border always have different colours. You can read more about the theorem in the Plus article The origins of proof IV: The philosophy of proof. This problem first came to the attention of mathematicians in 1852, and in 1879 Alfred Kempe published his "proof" in Nature and the American Journal of Mathematics. Unfortunately, in 1890, Percy Heawood found an error and it was another 86 years until Kenneth Appel and Wolfgang Haken came up with their own "proof". Appel and Haken assumed that there was a map which needed five colours, and then showed that this led to a contradiction. Their proof started by assuming that if there are several five-colour maps, you can choose the one with the smallest number of countries. They then showed that this map must contain one of 1936 possible configurations, and they also proved that every one of these configurations can be reduced to a smaller configuration which also needs five colours. This is a contradiction because we assumed that we started with the smallest five-colour map.
The problem with this proof is that part of it was achieved by using a computer to analyse many of the 1936 configurations. The proof, if printed, would be so long that no one could ever actually read it to check that it was correct. If a proof can not be checked, then most mathematicians agree that is it is not a proof at all.
In contrast to the four colour theorem proof, Trakhtman's proof of the road colouring problem is beautiful in its elegance and simplicity. Trakhtman solved the problem the old-fashioned way without computers by simply pondering on the problem and then scribbling down notes. Trakhtman's work is even more remarkable given his journey to becoming Professor of Mathematics at Bar-Ilan University. As a Russian scientist who immigrated to Israel in the 1990s, Trakhtman had to work in maintenance and night security for four years to support himself before being appointed by Bar-Ilan University's Department of Mathematics. The solution could have real-life applications in mapping and computer sciences.
You can read Trakhtman's proof on the mathematics arXiv.
Comments
Anonymous
The four color theorem was proven in 1976 by Kenneth Appel and Wolfgang Haken by using a computer.
http://en.wikipedia.org/wiki/Four_color_theorem