Discovering new primes
You may think that searching for new prime numbers is a job for super-computers. However, on 13th November 1996, Frenchman Joel Armengaud discovered a new one using his humble PC. He was taking part in the Great Internet Mersenne Prime Search (GIMPS), the brainchild of George Woltman, a computer programmer from Orlando, Florida.
Woltman set up an internet site to distribute a free program for testing Mersenne numbers for primality (see box). As a result, over 700 people from all over the world have taken part. "It gives the average person a chance to participate in the scientific discoveries of tomorrow", said Woltman.
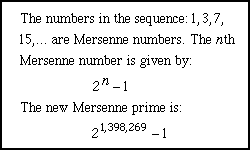
The new prime is a staggering 420,921 digits long. That's enough to fill a 200 page novel. But despite its size it's still only the 35th one of its kind to be discovered. "Finding this new Mersenne prime was quite a thrill! Mersenne primes are very rare, there was only one chance in 35,000 that this Mersenne number would turn out to be prime," said Armengaud.
Despite their rarity mathematicians think there are infinitely many such primes, though this is unproved. In fact, there are many Mersenne numbers smaller than the new prime that remain untested. The message is clear: you too could join the likes of Euler and go down in history as the person who discovered a Mersenne prime.
For more information about GIMPS see http://www.mersenne.org/prime.htm.