
From dust to us

This article is part of the Researching the unknown project, a collaboration with researchers from Queen Mary University of London, bringing you the latest research on the forefront of physics. Click here to read more articles from the project.
In his poem, written about 13 BC, the Roman poet Horace was comparing our brief human lives to the seemingly eternal renewal of the Earth through the cycle of the seasons and the waxing and waning of the moon. He was right about the dust part, but not just for us humans. The Earth and Moon are far from eternal and they, along with every other planet and star in the Universe, began as particles of dust.
Nebulous beginnings
Our Solar System started as a nebula — a giant swirling cloud of gas and dust. As more and more particles clustered together in the core of the nebula, their gravitational attraction pulled in yet more material. Finally the temperature at the core became high enough to trigger nuclear reactions and our star, the Sun, was born.
The cloud of gas and dust flattened into a disc spinning around the Sun and some of the dust particles within it began to clump together. As these clumps accreted more and more particles they too gathered their own gravitational fields, drawing in yet more material until they formed into the planets Mercury, Venus, Earth and Mars. "They are small rocky planets with quite high densities, made out of rocky material and metals," says Richard Nelson, as he told us about this nebula hypothesis for how planets form. Nelson is Professor of Astronomy and Mathematics, and the Director of the Astronomy Unit at Queen Mary University, London.
"Then if we go across the asteroid belt we come to the giant planets in our solar system: Jupiter, Saturn, Uranus and Neptune." Giant planets have a better chance of forming in this region, further out from the star, as the temperature there is colder. In addition to the metal and silicate materials that formed the rocky planets, additional icy particles, composed primarily of water ice, can be found in these colder regions. "This allows you to build bigger bodies because effectively [there is an] increased amount of solid material available for building large planets."
"What we believe in our own Solar System is that large cores, consisting of rock and ice, formed by this process of sticking together over a million years or so," says Nelson. "Eventually we ended up with a core of material which was large enough to pull the gas from the surrounding disc onto the planet to form the gas giant and ice giant planets we see today." The gas giants, Jupiter and Saturn, are primarly made of gas with icy, rocky cores at their centre. Uranus and Neptune, known as the ice giants also have a core made out of icy and rocky material mixed together and then a relatively modest envelope of hydrogen and helium sitting on top.
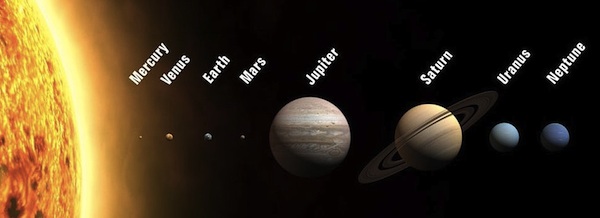
The planets of our Solar System (Image by Kwamikagami CC BY-SA 3.0)
Planets on the move
Our Solar System provides typical examples of the different types of planets that are formed at different distances from a star. And the nebula hypothesis also suggests that planet building doesn't occur too close, or too far from a star. "It takes a long time to build a planet far away from a star," says Nelson. "Planet building is best done relatively close to a star, but not so close that it is too hot. Near to the star the temperature is very high, beyond 2000 degrees Kelvin. We believe that at those temperatures the small dust grains actually vaporise. So very close to a star there isn't the possibility of building a planet in situ."
So it might have seemed surprising that the very first planet discovered to orbit around star other than our Sun told a very different story. "In 1995 the very first bona fide planet orbiting around a sun-like star was found outside of our Solar System," says Nelson. The star was called 51 Pegasi and the planet, called 51 Pegasi b or 51 Peg for short, takes just four days to orbit around its star. 51 Peg appears to be a gas giant just like our own Jupiter, with about half the mass. Except that our Jupiter orbits the Sun with a period of 4,500 days, about 1000 times slower than 51 Peg. This is because 51 Peg is very, very close to its star, at a distance of just eight million kilometres. This is well inside Mercury's orbit of our own Sun, putting 51 Peg in the hot zone of its solar system where the Nebula hypothesis says it's not possible for planets to form.
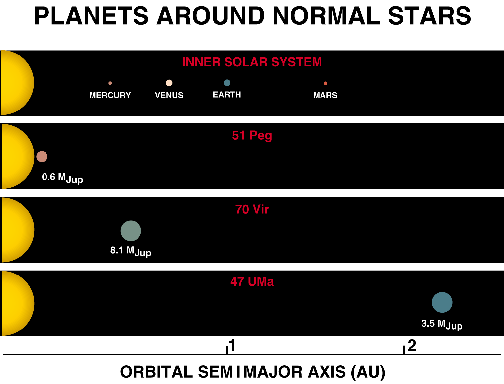
Four of the first known planetary systems: our Solar System, 51 Pegasi, 70 Virginis and 47 Ursae Majoris. (Image courtesy NASA)
This was just the first discovery of such a hot Jupiter-like planet. "That discovery has lead to an enormous increase in research in trying to, first of all find planets outside of our solar system orbiting other stars; trying to characterise what those planets are like and also trying to understand how they formed," says Nelson. "And the interesting thing is that the planetary systems [we've found] are very diverse." As well as many examples of hot Neptunes and hot Jupiters, like 51 Peg, we've also discovered planets whose orbits are much further from their stars, say 50 to 100 times further away than planets in our Solar System.
But to some astronomers and mathematicians, this variety of orbital distances was not so surprising. In the 1970s and 80s groups of researchers, including Nelson's PhD supervisor John Papaloizou and his colleague Doug Lynn, developed models to explain how planets form. And their models predicted the hot Jupiters we have since discovered. "There were very clear predictions within their work that planets should migrate once they form within the gaseous discs," says Nelson. "Of course it was a real conundrum to understand why the one planetary system that we knew about [at the time], our Solar System, didn't show any signs of orbital migration." Even today researchers are still trying to understand what has made our Solar System so stable in comparison to the many other planetary systems we've found.
In a spin
The discovery of 51 Peg was evidence that planets migrated towards or away from the star once they had formed. And the explanation of why this could happen has something to do with childhood games of spinning balls and playground swings.
Kepler's 3rd law and speed
In the 16th century the mathematician and astronomer, Johannes Kepler, discovered three laws that governed the motion of the planets. (Find out more about Kepler's laws of planetary motion.) His third law said that for any planets orbiting the same star, the ratio of the squares of their orbital periods (the orbital period is the time it takes a planet to orbit its star) was the same as the ratio of their average distances from the star. (This is the law Newton used to develop his theory of gravity some time later.)
Mathematically we can write $$ \frac{T^2}{R^3} = C $$ for any planet, where $T$ is how long it takes to orbit the star in seconds and $R$ is the average distance of the planet from the star in metres (we need to use an average as planets orbit in an ellipse around their stars, though in our solar system most of these ellipses are pretty close to circles). For every planet this ratio is equal to a constanct $C$, which has the value $$ C=\frac{4\pi^2}{GM} $$ where M is the mass of the star and G is the gravitational constant. Plugging in the values for the Earth's orbit around the Sun (R=149598261000 m, G=6.67834x10-11 and M=1.98855x1030 kg) gives an orbital period for Earth of 31,558,609 seconds or 365.26 days.
From this we can also calculate the speed at which the Earth orbits the Sun. In 1 year (equal to 31,536,000 seconds) the Earth travels, roughly, $2\pi \times R = 2\pi \times 149598261$ kilometres, which equates to around 30 kilometres per second.
Planets have an angular momentum from the speed at which they orbit around their star. This angular momentum provides an effective force (called the centrifugal force) which balances the gravitational pull of the star, stopping the planet from falling in towards it.
"Imagine I am spinning a ball on a piece of elastic," says Nelson, explaining how changing angular momentum affects planetary orbits. If you spin the ball relatively slowly the elastic won't stretch very much. "The orbit of the ball around my hand is relatively small, because I'm not giving it much angular momentum. Now if I start to speed up I am giving more angular momentum to the ball and the elastic will stretch and [the ball] will orbit further from my hand." So a ball (or a planet) with more angular momentum will have a larger orbit than a ball (or a planet) with a smaller angular momentum.
"We are moving around the Sun with a speed of abut 30 kilometres per second," says Nelson (see the box for the calculation). "Imagine I was to somehow apply a brake to the Earth and start to slow it down, to lose angular momentum. That means that the Earth's [rotational] energy would be reduced and the gravitational field of the Sun becomes more dominant, so [the Earth] would tend to move in towards the Sun."
Putting the brakes on
We don't believe anything put the brakes on Earth and it has stayed pretty much where it formed all those millions of years ago. But something did put the brakes on 51 Peg and the other hot Jupiter and hot Neptunes that have been discovered. When they formed in the gaseous disc circling around their stars their gravity began to interact with the disc itself with some beautiful consequences.
The gas disc is orbiting the star, very much like the planets would be. In our solar system Mercury, much closer to the Sun, is moving around the Sun much faster than Earth or Jupiter. "The gas and particles in the disc shows the same kind of speeding up closer to the star and slowing down further out," says Nelson.
"Imagine you are just sitting somewhere within the disc, sitting happily on a planet going around in a circular orbit." If you look at the material in the disc outside of your position, away from the star, it is travelling around the star more slowly than you. If you look at the material in the disc inside of your position, closer to the star, it is overtaking you and moving around the star much faster." In effect you'd see the material further from the star shearing past in one direction and the material closer to the star shearing past in the other direction."
"As the material comes past the planet [in either direction] it feels the gravity and gets pulled towards the planet." However, this material doesn't always actually hit the planet but can move away again, creating a kind of recoil motion. The recoil motion gives rise to what are effectively soundwaves travelling through the disc. And these soundwaves move away from the planet, creating a spiral pattern in the disc.
"The mathematics describes the excitation of waves in the disc by the gravitational perturbation due to the planet. Just like when you drop a stone into a pond and you get a rippling effect, or a ship ploughing through the ocean creating a bow wave which then propagates. It is very much the same process, the same physics and mathematics is involved," says Nelson.
Swings and roundabouts
The reason this gravitational interaction between the planet and the disc causes the planet to spiral in is down to the concept of resonance, something we're all familiar with from playing on the swings in the playground. If you are pushing someone on a swing, and you push it randomly at any old time, the swing will wobble erratically in response. But if instead you watch the speed of the swing and time your pushes to the period of the swing, you are pushing it at its so called natural frequency. The swing responds more strongly to each of these well-timed pushes, increasing the amplitude — that is the height — of the swing. This is the concept of resonance.
"It turns out, for rather complex reasons, that there are positions in the disc where the gas has an orbital period which is resonant with the orbital period of the planet. The gas responds, at those particular locations, much more strongly than it does at other locations. We call these Lindblad resonances. At these locations the waves are excited most strongly. It is because the orbital periods are just right relative to the planet's orbital period that the gas feels a very strong force. As the gas comes by the planet it feels like it is being pushed, just like the [swing] is being pushed."

Resonance is fun (Image by Douglas Walker CC BY-NC 2.0)
The result is a spiral of increased density in the outer disc, spiralling away from the planet. The increase in density in the disc means a corresponding increase in the gravitational field there pulling back on the planet like a brake. "The material which is orbiting interior to the planet is going faster than the planet. The spiral wave which is generated there pulls in front of the planet, acting like an accelerator. You have got an accelerator pulling in one direction and a brake pulling in the other direction."
But because the resonances sit closer to the planet on the outside of the disc than they do on the inside, this makes the brake stronger than the accelerator so in this case the planet loses angular momentum and falls towards the central star.
"We have this tug of war and this balancing act. What we know from our recent work, here at Queen Mary, is that it depends on where you are in the disc as to whether or not the outward migration is stronger or the inward migration is stronger. It also depends on the age of the disc as well as on what its physical conditions are," says Nelson.
"The picture that we are developing is getting very, very complicated. It matters how big you are, where you are and when you are there. The details haven't been fully worked out and this is an area of very active ongoing research. I would say it is one of the most important problems that we are trying to understand at the present time in planetary formation theory. Once we understand this in more detail, we will hopefully be able to explain all of the extrasolar planetary systems that we see. We will be able to tell a story about how those planetary systems came into existence and why the planets are orbiting at the locations where they are seen to be orbiting."
Born from dust, described by maths
Mathematics plays a fundamental role in this research. "The laws of physics themselves are encoded mathematically," says Nelson. "When we develop our theories of planetary migration or planetary formation we are effectively solving a set of equations. These equations take different forms; normally partial differential equations or ordinary differential equations. [These equations] encode how the disc responds when a planet is embedded within it, for example. And these equations give rise to solutions which predict that the presence of a planet in a disc creates a nice spiral pattern [in the disc]."
Sometimes these equations can be solved analytically, with a pen and paper. But more often this is not feasible or even possible. (You can read about one example of this in Mathematical mysteries.) Instead computers are used to predict solutions and create simulations of how planetary systems evolve. "By encoding these equations and putting them on the computer, we can actually follow the evolutions, for example, of a planet as it migrates through a disc. We can explicitly simulate that process on a computer."
Queen Mary is one of the leading groups in this area: "We are making significant contributions to understanding how planets actually migrate here at Queen Mary," says Nelson. And with the increasing evidence from observational astronomy, it won't be long before the Queen Mary teams' beautiful computer simulations of the births and early lives of planets are seen in the skies above.
About this article

Richard Nelson is a Professor of Astronomy and Mathematics, and the Director of the Astronomy Unit, in the School of Physics and Astronomy, at Queen Mary University of London.
Rachel Thomas, Editor of Plus, interviewed Richard Nelson in London in July 2014.
