Pour yourself a cool glass of water from the fridge. Before you drink it, take a moment to consider how you might describe it. Physically there are two different approaches you could take. You could measure something about the glass of water as a whole – say measure the temperature of the water or calculate the volume contained in your glass. This thermodynamic approach describes the macroscopic state of the water. Alternatively you could consider the microscopic state of the water and use the language of statistical mechanics to take into account the position and velocity of all the water molecules in the glass. (You can find out more about these two approaches in the previous article.)

A microstate in statistical mechanics describes the positions and momentum of all 8 x 1024 (approximately) water molecules inside the glass. You could imagine rearranging the configuration of these water molecules, perhaps by giving it a gentle stir, and this not affecting some macroscopic measure, such as the temperature of the water. This would mean that more than one microstate could correspond to the same macrostate. "It's clear that there are many, many microstates that will correspond to the same macrostate," said Robert de Mello Koch, from Huzhou University (China) and University of the Witwatersrand (South Africa), in his talk at the Isaac Newton Institute for Mathematical Sciences.

Ice has low entropy as only a limited number of configurations of the water molecules is posible

This correspondence between the micro and macro scales brings us to the hero of our story – entropy. The entropy of a physical system, such as the entropy of our glass of water at a certain temperature, is a measure of how many microstates of the system correspond to a given macrostate.

As we've already observed many microstates are possible for our glass of liquid water, so its entropy will be high. But what if we cooled our water, so that it became a block of ice? The molecules in a block of ice are fixed in a rigid lattice – only certain configurations of the water molecules are possible, reducing the number of microstates that can possibly correspond to this lower temperature. So if we freeze our glass of water we will significantly lower its entropy.

Get in order for low entropy

Entropy reveals the order, or disorder, in a physical system (Image by Tweek – CC BY-SA 2.0

One way of getting a grip on entropy is to consider it as a measure of the order, or disorder, of the system. It's clear that the molecules in the block of ice, which has low entropy, are more ordered than the molecules in the glass of water, which has higher entropy. "This idea that at low temperatures things are ordered and at high temperatures things are more disordered, where there's a higher entropy state, has got an enormous amount of explanatory power," said de Mello Koch.

Now you've got your glass of water, or your glass of ice, look on the outside of your fridge for an example of entropy as a measure of order. You might have magnets holding various notes, bills and photos to your fridge. Each atom in a fridge magnet can itself be thought of as a little bar magnet, represented by a little arrow indicating the orientation of the atomic magnetic field. All these little arrows are arranged in a grid inside the fridge magnet, with the little magnetic fields represented by these arrows added together to give the total magnetic field in the whole fridge magnet.

Schematic depiction of the atoms in a magnet. (Image by Michael Schmid – CC BY-SA 3.0)

You might remember from playing with bar magnets that they prefer to be aligned – it takes a lot more effort to hold two bar magnets with the repelling ends together, than to let them flip to align and point in the same way. So for ferromagnetic materials that are used to make fridge magnets, it takes much less energy for the atoms to be aligned in this way.

"Once you have picked the direction of the first arrow, then every single other arrow inside the state must be aligned with it," said de Mello Koch. So for each possible alignment of the magnetic field of the fridge magnet as a whole, very few configurations of the arrows of the atoms inside are possible. This highly ordered state means that very few microstates are possible, and the fridge magnet has very low entropy.

How large can entropy be?

What if instead you had a random, disordered configuration of arrows, showing the orientation of the particles in the grid pointing in random directions. What is the entropy of this system?

The entropy of a physical system amounts to counting all the possible microstates. To make that counting problem as simple as possible let's limit ourselves to each particle being oriented either pointing up or down.

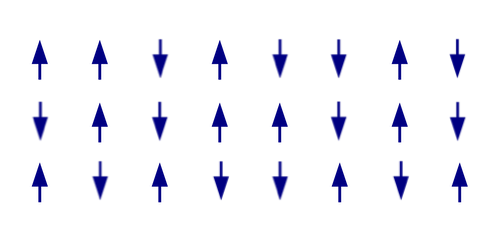
Schematic depiction of randomly oriented atoms. (Image adapted from one by Michael Schmid – CC BY-SA 3.0)

The highest possible entropy would be if the system were in a macrostate where every configuration of our particles was possible. Each particle in the grid can point up or down, so we have 2 possible directions for the first particle, 2 for the second particle, 2 for the third and so on. For our example above, we have 24 particles in our grid, so we have 2²⁴ different choices for the orientation of the particles, giving 2²⁴ microstates. If we had a grid of $n$ particles which could point up or down, we would have $2^n$ microstates.

The entropy, $S$, is defined as $$ S=k \ln{W} $$ where $W$ is the number of microstates and $k$ is a constant called Boltzmann's constant. (You can read more about how entropy is defined here.)

So the maximum possible entropy for a grid of $n$ particles will be $$ S_{max}=k\ln{2^n}= k n \ln{2}. $$ The maximum possible entropy is proportional to the size of the system, as described by the number of sites of particles in our grid. "If I was to double this area, I'll double the number of sites, which means that will double the entropy," said de Mello Koch. "If I multiply the area by 10 I'll multiply the number of sites by 10 and the entropy will be multiplied by 10." This extends to three-dimensional grids too – the entropy is proportional to the volume of the system.

Entropy of black holes

In the previous article we saw that the laws of black hole mechanics discovered by Stephen Hawking and his colleagues were actually equivalent to a thermodynamic description of black holes. An example of this dual description is Hawking's area theorem, which states that, no matter what happens to a black hole, the area of its event horizon will never get smaller. This looks a lot like the second law of thermodynamics, which said that the entropy of an isolated physical system never decreases.

The theoretical physicist Jacob Bekenstein was inspired by Hawking's area theorem to suggest that the entropy of a black hole is proportional to the area of its horizon. Beckenstein's idea was controversial at first, but when Hawking tried to dispute it he in fact did the opposite and confirmed it was true. (You can read more in our interview with Bekenstein, and our article Celebrating Stephen Hawking.)

"This should be making you feel a little uncomfortable," said de Mello Koch. Previously we saw that entropy is proportional to the volume of the system. "Now all of a sudden for black holes we find the entropy is not proportional to the volume of the black hole – it's actually proportional to the area of the horizon of the black hole. This looks puzzling. But does it actually point to a problem with the laws of physics?"

The paradox of black hole entropy

We appear to have a fundamental problem. Imagine a region of space of a certain volume, $V$, that contains some matter, but not enough to produce a black hole. Then the entropy of this region, according to our argument about the maximum possible entropy, is proportional to the volume $V$.

Now if you squash in enough matter (or equivalently energy) into that region you will be able to form a black hole. But if you've got a black hole filling this region then its entropy will now be proportional to the area of the boundary of the region – that is, the event horizon of the black hole.

"So that means we went from an entropy proportional to the volume of the region – added [mass] to form the Black Hole which filled the region – and landed up with an entropy proportional to the area of the boundary of the region," said de Mello Koch. "If it's a big enough region the volume is always going to be bigger than the area. So by adding [mass] to the region the entropy has gone down."

This is inconsistent with the second law of thermodynamics – that entropy never decreases. We must have done something wrong when describing a black hole in terms of entropy. But perhaps this isn't surprising given that such a description of a black hole in terms of statistical mechanics takes us into the realms of quantum gravity – one of the most pressing problems in modern physics.

De Mello Koch's talk was part of a research programme hosted by the INI to bring together mathematicians and physicists to advance our understanding of black holes and quantum gravity. To unravel this paradox of black hole entropy we have to explore an entirely new idea – the holographic principle – that might give us a way to understand quantum gravity.

Find out in the next article why this "bizarre" principle might be just the description of nature we need.

About this article

This article is based on Robert de Mello Koch's Rothschild Lecture, part of the research programme Black holes: bridges between number theory and holographic quantum information at the INI in October 2023. You can read more about this programme here.

This content was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.