Imagine you're back in science class and you've been given a glass box containing some gas, and you've been asked to describe it. What sort of description would you come up with? Many of us would measure and describe the gas as a whole - perhaps measuring the temperature of the gas, the pressure of the gas, and calculate the volume of the box containing it. This coarse grained, macroscopic description fits into the approach of thermodynamics.

From steam engines

Thermodynamics – thanks to the steam engine (Image in public domain)

"Thermodynamics was invented by engineers studying steam engines and energy conversion problems," said Robert de Mello Koch, from Huzhou University (China) and University of the Witwatersrand (South Africa), in his talk at the Isaac Newton Institute for Mathematical Sciences. These engineers measured these macroscopic variables, such as temperature, pressure and volume, experimentally, and came up with laws to explain their experimental data. "This is a very empirically driven subject, it has an engineering feel to it." (You can read more in our short introduction to thermodynamics here.)

The gas, of course, is actually made up of bazillions of atoms whizzing around inside the box and banging into each other. We could use our knowledge of these microscopic particles and how they interact with each other in our description of the gas. This approach, called statistical mechanics, acknowledges the microscopic nature of the system you are describing. (You can read more about statistical mechanics in our introduction here.)

"[When] there are so many particles in the system, it makes sense for you to start using statistics and probability theory," said de Mello Koch. With this statistical approach you can start to define quantities as averages over the entire system, which takes you back into contact with the thermodynamic description of your system.

There's clearly a relationship between these two approaches: "Thermodynamics gives a coarse grained description, and is very empirically driven. In statistical mechanics you take account of the fact that you want to give a more fundamental description of the system in terms of its constituents. And one of the goals of statistical mechanics is to put the laws of thermodynamics onto a firmer footing – to start from the dynamics of these fundamental particles in statistical mechanics and to derive the empirical laws [of thermodynamics] that you found from experiment."

General relativity

Now we need to imagine ourselves in a very different place – out there somewhere in the Universe observing stars, planets and gravity in action. To describe anything at this scale we need to use Einstein's theory of general relativity. In this theory Einstein said that what we think of as three-dimensional space, and time, are actually both just different aspects of something called spacetime. And he said that gravity isn't a force one object imposes on another, instead it results from the curvature of this spacetime.

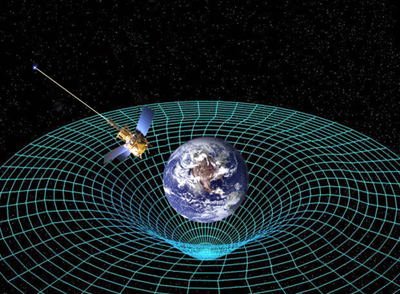
Gravity is the manifestation of the curvature of space and time. Image courtesy NASA.

General relativity tells us that massive objects warp or bend spacetime. If you put something massive in space – let's say a planet like Earth – then space around it gives a little. And this curvature of spacetime, induced by massive objects within it, directs the paths of objects moving around in spacetime. When something else moves close to a planet – say the Moon moving near the Earth – it feels this curvature in space and rolls around the planet like a marble rolling in a bowl. Einstein’s theory of gravity was radically new — it unified the concepts of space, time, mass and gravity in a single elegant geometric framework. (You can read more about general relativity in our introduction here.)

Black holes

The most extreme example of curvature of spacetime is near black holes. "A black hole is literally a hole in spacetime," said de Mello Koch. Black holes are formed when a lot of mass is concentrated in a tiny region of space – imagine the mass of the Earth concentrated into a sphere that is just a few centimetres wide. Then the force of gravity is so strong within this region that nothing, not even light, can escape, hence the name "black hole". The edge of the black hole is called the event horizon. This is a boundary of no return: "If you pass the event horizon you're out of the Universe and never coming back. So believe me when I tell you a black hole is the worst kind of a hole that you can fall into!" (You can read more about black holes here.)

They were first discovered mathematically as solutions to Einstein's equations of general relativity, but they have since been observed in our Universe.This is the first image of a black hole that was ever taken, released in 2019. Image: European Southern Observatory., CC BY 4.0.

In the 1960s and 70s, during what became known as the "golden age of black hole theory", the famous physicist Stephen Hawking and colleagues discovered that general relativity led to some simple laws governing the behaviour of black holes. And that these laws of black hole mechanics looked surprisingly like the laws of thermodynamics.

One example is Hawking's area theorem, which states that, no matter what happens to a black hole, the area of its event horizon will never get smaller. For example, if two black holes collided and merged, the area of the event horizon of the resulting black hole would be at least the sum of the area of the horizons of the original black holes. Hawking's area theorem looks a lot like the second law of thermodynamics, which says that the disorder of an isolated physical system (measured by a number called entropy, which we will explore more in the next article) never decreases.

"There's a whole list of laws of black hole mechanics and they look very similar in nature to the laws of thermodynamics." But since black holes were thought to be simple objects that didn't come with any degree of disorder — they were just black — this was thought a mere analogy without deeper meaning. "But all of that changed with the groundbreaking work performed by Stephen Hawking here at Cambridge."

Quantum gravity

This analogy became a physical reality when Hawking showed that black holes aren't just black after all. Instead — just like a hot cup of tea left sitting to cool down — they emit thermal radiation into their environment. His theory of what has come to be called Hawking radiation isn't a result of observational evidence, but of mathematics. While pondering a particular puzzle that was intriguing physicists at the time, Hawking considered a hypothetical universe consisting of a single black hole. General relativity makes it possible to study such imaginary worlds, but Hawking also brought in the theory of physics that describes the world at very small scales – quantum mechanics. (You can read a very short introduction to quantum mechanics here.)

When applying quantum mechanics to matter outside the black hole, Hawking discovered that some thermal radiation should be emitted by the black hole, and that this should be true for black holes in general. Admittedly, the temperature of that radiation, now called the Hawking temperature, is nowhere near that of a hot cup of tea: instead it's incredibly low, only a tiny fraction above absolute zero. But the fact that there should be any radiation at all stunned the physics community.

"And as usual [for a thermodynamic object] you can read off a temperature," said de Mello Koch. And this temperature exactly matches the surface gravity of the black hole – the acceleration due to gravity an object would experience at the surface of the black hole. "So in this way with Hawking's work we learnt that the laws of black hole mechanics don't just look like the laws of thermodynamics, they actually are the laws of thermodynamics for black holes."

And this takes us back to the very beginning of this article, and also to the very limits of physics. "We said that thermodynamics is the coarse grain, sort of rough approach to the physics. But there's a more careful approach – statistical mechanics – in which we try to describe the fundamental constituents of our objects and how they interact," said de Mello Koch. He and his colleagues are trying to derive the statistical mechanics of black holes, which would amount to understanding one of the most pressing problems in modern physics: quantum gravity, a mathematical framework that would comprise both general relativity and quantum mechanics. Such a framework has so far eluded physicists and mathematicians.

De Mello Koch's talk was part of a research programme hosted by the INI to bring together mathematicians and physicists to advance our understanding of black holes and quantum gravity. "One of the goals of my community is to advance science in one of its most fundamental directions – the discovery and understanding of new physical laws."

Find out in the next article how using statistical mechanics to describe black holes might lead us closer to the problems, and the solutions, to understanding quantum gravity.

About this article

This article is based on Robert de Mello Koch's Rothschild Lecture, part of the research programme Black holes: bridges between number theory and holographic quantum information at the INI in October 2023. You can read more about this programme here.

This content was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.