Researchers from the University of Chicago have been suggesting that readers rip pages from the journal Physics Review Letters. However, they are not promoting vandalism - they are just interested in the surprising resistance of paper to crumpling.

Take any ordinary piece of paper with sides much longer than the thickness of the paper - a sheet of A4, say - and crumple it up in your hands. No matter how tightly you squeeze, the resulting crumpled ball will still contain more than 75% air. As the sheet is crushed, energy is stored in all the creases and corners that are created. These resist the force you are exerting, and if you can overcome this resistance, the crumpled ball of paper must collapse, forming increasingly many more creases and points. Eventually, the energy stored in the crumpled ball will be so great that you would need to exert a huge force just to make it a tiny bit smaller.

Or so the physicists from the University of Chicago thought. For an experimental simulation, they crumpled up a thin mylar sheet and placed it in a cylinder with a weighted piston on top to exert a constant force. Surprisingly, the crumpled mylar sheet was not quickly squeezed to a final size by the force of the weight - in fact, it was still decreasing in size after three weeks! They discovered that the size of the mylar ball decreased logarithmically over time, asymptotically approaching a limiting size.

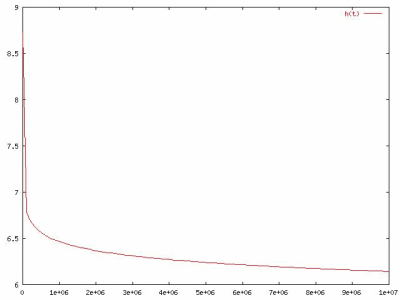
The size of the crumpled ball decreasing over time

This meant that the energy stored in the crumpled structure of the mylar sheet was unexpectedly dissipating in some way over time, meaning that the force of the weight was able to continue to make the crumpled ball smaller. However, as the size of the ball decreased, so did the rate at which the weight could compress it. So, despite the unexpected dissipation of energy, the crumpled ball did indeed, as expected, resist further crumpling the smaller it got.

The physicists now believe that the question of how an applied force affects the ultimate size of a crumpled sheet will have a more complicated answer than was first thought. They will need to explain how the energy dissipates from the crumpled ball - whether because of friction caused by the folds of the paper pushing against each other, or for some other reason. So in future libraries may have to be more lenient on book-vandalising physicists, as it's all in the name of science.