
Forget Sudoku and smile for the camera
It's often claimed that solutions to difficult problems can come to you when you're thinking of something entirely different. Physicist Veit Elser from Cornell University is a case in point: he accidentally found a recipe for solving Sudoku puzzles while trying to take pictures of really small things. The algorithm he and his colleagues developed for a microscopy technique called x-ray diffraction microscopy can solve any Sudoku puzzle you care to throw at it.
This in itself isn't a new thing. Algorithms for solving Sudoku have been around for a long time. But in realising that the difference-map algorithm he and his colleagues developed to analyse waveforms — in this case light waves — can double up in this way, Elser shed new light on how amazingly versatile the algorithm could be. "As a personal benefit," Elser says, "I can now explain to the person on the street what I do!"
The reason the difference-map algorithm works for both Sudoku and for creating images of tiny things (such as single cells) is that both reduce to solving problems whose solutions must satisfy two independent rules, or constraints. In Sudoku, these constraints are easy to pin-point. One way of phrasing them is: fill the numbers between 1 and 9 into a 9 by 9 grid so that
- each number appears exactly once in each row and column, and
- each number appears exactly once in each 3 by 3 sub-grid.
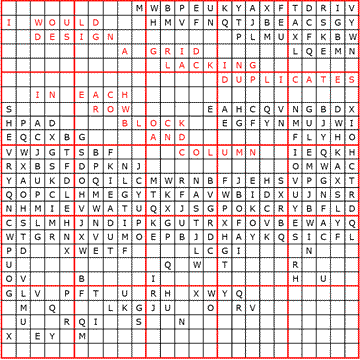
This is a version of Sudoku designed by Elser's algorithm. Your task is to fill the letters from A to Y into the 25 by 25 grid so that every letter appears exactly once in each row, column and 5 by 5 sub-grid. The solution will spell out the name of one of the founders of Cornell University.
But how does creating an image of something such as a single cell lead to a "two constraint puzzle"?
Really small objects can't be captured by an ordinary microscope because they are smaller than the wavelength of ordinary visible light. In x-ray diffraction microscopy the object to be imaged is therefore bombarded with x-rays, which have a much finer wavelength. The way the light is scattered, or diffracted, by the object then contains the information needed to recreate a magnified image. If you were using an ordinary microscope the job of re-assembling this information to give an image would be achieved by a lens. This is impossible if the object is too small. All you can do is measure the scattered rays directly, and then re-combine them using a mathematical process called Fourier synthesis.
Fourier synthesis relies on the fact that any waveform can be expressed as the sum of individual sine and cosine functions. These constituent functions each have their own frequency, amplitude and phase (see figure 1). If you know what these are, you can re-construct the original waveform simply by adding up its constituent parts. In our example of x-ray diffraction, the constituent waves come from the scattered rays, which you measure, and adding them up gives a waveform which you use to create the image.
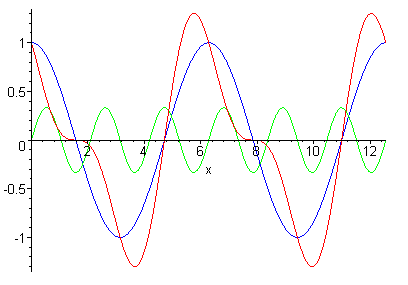
Figure 1: a sine wave of the form a sin(bx+c) has amplitude a, frequency b and phase c. The blue graph represents the wave sin(x+π/2), the green graph represents the wave sin(3x)/3, and the red wave represents their sum.
The problem is that when you are measuring the scattered rays, you lose vital information about their phase. If you simply resort to guess work, and randomly compute the phases in some way, then you are likely to end up with a meaningless image, or noise as mathematicians call it. Just like randomly filling numbers into a 9 by 9 grid is unlikely to give you the solution to a Sudoku puzzle. What you need are extra clues: rules that the phases have to obey. "People used to say that's an impossible problem," Elser says. "Then people got to thinking about the fact that there are going to be constraints coming from some rather mundane facts — that in principle will make the problem of deducing the phase like the solution of a solvable puzzle."
And the constraints here turn out to be very mundane indeed: one of them simply comes from the fact that the object in question has a well-defined boundary. In any image of the object, nothing should appear outside of that boundary, in other words, the pixel values there should be zero. "If I set up waves with known amplitudes and synthesize them, I'll find that for essentially all random combinations of phases, the thing I get is an object not confined," Elser says. "It takes a very clever combination of the phases of all those waves to add up to something in only one region; and cancel out everywhere else." The other constraint seems even more obvious: the waves you feed into your Fourier synthesis mechanism should have the amplitudes you have measured in your scattered waves.
With these two constraints in place, the imaging problem becomes a puzzle that Elser's algorithm can solve, just as it can solve any Sudoku puzzle. It will chomp through the calculations and spit out exactly those phases that give the correct image. Elser and colleagues have already used the algorithm to produce images of a single yeast cell, which have been published in a paper in the Proceedings of the national academy of sciences.
And where does all this leave Sudoku maniacs? The existence of a clever new algorithm probably won't cure them of their disease... unless they are true mathematicians: they often lose interest in a problem as soon as they know that a solution exists, even if no-one knows what that solution is!
Further reading
- See the Plus article Anything but square: from magic squares to Sudoku for more information on Sudoku, its relatives and predecessors.
- Try your hand a solving a new version of Sudoku which is this issue's puzzle.
- The Plus interviews with an audio software designer and a computer music researcher explain how Fourier analysis is used to understand sound.
- If you would like to find out more about x-ray diffraction, read this article about how it is used in crystallography.