2015 is a special anniversary for mathematicians. It is the bicentenary of the birth of George Boole, one of the founding fathers of our modern computers.

George Boole (1815-1864).

The story of George Boole (1815-1864) is an extraordinary example of collaboration across the centuries. Boole's work provided the foundations for today's computers and mobile phones, yet he died many years before the first computers were invented. How did a mathematician who lived, and died, in the nineteenth century have such an impact on our twenty-first century technology? This is the tale of self-taught mathematician George Boole and the modern day engineers who recognised the power of his ideas.

Boole's early life

George Boole's early life did not mark him out as a ground-breaking mathematician. Born in Lincoln in 1815, he was the son of a local cobbler and would have been expected to work in the family shoe making business as he grew older. But his father's business collapsed and Boole became a local school teacher instead. By the age of 19, he was already a head teacher, spending his evenings and weekends exploring his mathematical ideas. His initial writings appeared in the Cambridge Mathematics Journal and his work soon attracted the attention of the Royal Society. In 1844 Boole was awarded the Royal Society's Royal Medal for his paper On a general method of analysis. His increased profile led to the offer of a professorship in mathematics. Boole left behind his Lincolnshire teaching career and headed off to Cork University to pursue his mathematics full-time, and make the break-through that still impacts on our lives today.

The breakthrough

During his time in Ireland, Boole focused on combining logical deduction with algebra. He argued that the logical approach taken by the ancient Greek philosopher Aristotle and his followers was insufficient for addressing certain types of problems. He focused on those problems where individual statements, or propositions, could either be described as true or false. Boole's work required the development of a new branch of algebra and its associated arithmetical rules.

To introduce Boole's ideas, consider these two propositions:

A = David Beckham is a footballer

B = Quidditch is an Olympic sport

We know that one of them is true and the other is false (I'll let you decide which is which!). But what about the statement A AND B: David Beckham is a footballer AND Quidditch is an Olympic sport? It's clearly false! For it to be true, we would need each of A and B to be true, which isn't the case. Therefore, the statement A AND B is false. If we assign the truth value 0 to a false statement and the value 1 to a true one, then we can write the AND connective as a kind of multiplication: AB stands for A AND B, and since one is true and the other false, we see that AB has the truth value 0 x 1 = 0.

What about the statement A OR B? David Beckham is a footballer OR Quidditch is an Olympic sport? For this to be true only one of A or B needs to be true, which is the case in our example. Hence A OR B has a truth value of 1. We can write it as a kind of addition: A+B stands for A OR B, and since one is true and the other false, we see that A+B has the truth value 0+1 = 1.

These ideas also make sense if A and B swap their truth values, or if they are both true or both false. The tables below show the truth values for A AND B and A OR B for all possible truth value combinations. They also show the corresponding arithmetic operations, as defined by Boole. The only thing that makes Boole's arithmetic different from the arithmetic we are used to is that, for Boole, 1+1=1, rather than 1+1=2. But that's not too difficult a feature to get used to.

In the world of Boolean logic all statements are made up of smaller statements connected by AND and OR, and possibly also involving the NOT operation, which turns the truth value of a statement into its opposite: if the statement "David Beckham is a footballer" is true then the statement "David Beckham is NOT a footballer" is false.

Now that you know some of Boole's algebraic laws, you might like the following problem:

Although the problem could be solved in a number of different ways, such as using trial and improvement, Boole argued that his algebra provided a much more systematic approach to problem solving. For the above problem, you may have already noticed several key propositions that will help to solve the problem. For example, we know that X must be either red, white or blue. So, the proposition "X is red, white or blue" is true with the truth value 1. Likewise, the proposition "X or Y or Z is red" must also be true with the truth value 1. We also know that each colour is only used once so the proposition "X and Y are red" is false with truth value 0. Likewise, a counter can only be one colour so the proposition "X is red and blue" is also false with truth value 0.

Working in this way, I will leave you to complete the set of propositions and to use Boole's approach to solve the problem for yourself. We will publish an answer on Plus soon.

Collaborating across the centuries

Boole's binary approach found a powerful application over 70 years after his death, when the mathematician and engineer Claude Shannon realised that it provided the perfect description for electrical circuits. To see how, imagine an electrical circuit with two switches and a light bulb attached to it. The bulb comes on when a current flows through the circuit, otherwise the bulb is off. Each switch can be either on (closed) or off (open). In the left-hand figure below, the light will only come on if both of the switches are on. In the right-hand figure, the light will come on as long as one of the switches is on.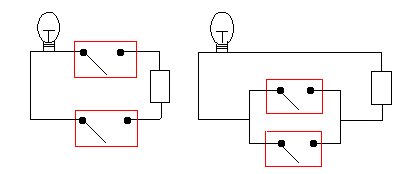

Engineers including Shannon realised that they could write 1 for the "on" position of the bulb and the switches and 0 for the "off" position. Writing down the possible combinations of 0 and 1 for the switches and the corresponding state of the bulb, what you get are exactly the truth tables of AND (left-hand circuit) and OR (right-hand circuit).

Using an inverter switch, which allows a current to flow when the switch is open, you can also mimic the truth table of NOT. This realisation meant that engineers could employ Boole's algebraic approach to design and to simplify their circuits.

Bur Shannon went further still: he suggested that all types of information — from words to pictures — could be described using strings of 0s and 1s. (In fact, it was Shannon who popularised the term bit we use to describe these digits today.) Since you can represent the logical AND, OR and NOT operations using electronic circuits, you can perform all sorts of logical tasks involving this information. It's this fact that the central processing units (CPUs) in our modern day computers are based on.

Whatever electronic gadget you use, it is based on the binary system and algebraic approach to logic first proposed by George Boole. A man who lived and died several years before the first light bulbs came on the market played a pivotal role in the development of the circuitry of our modern world.

Explore further

If you would like to learn more about electronic switches and would like to have a go at building your own circuits, see this activity on our sister site NRICH.

If you would like to try some more challenging activities using logic and electronic circuits, see these activities (also on NRICH):

• Truth tables and electronic circuits
• Logic, truth tables and switching circuits challenge
• Adding machine

About the author

Ems Lord is director of our sister site NRICH. She joined the NRICH team in 2015, following her previous role leading one of the country's largest Mathematics Specialist Teacher Programmes. Ems has taught mathematics across the key stages, from early years to A Level Further Mathematics, and has worked in a variety of settings including a hospital school. Her previous roles include supporting schools as a leading mathematics teacher, local authority consultant and as a chartered mathematics teacher. Ems has taught mathematics education on both BEd and PGCE teacher programmes and she is currently working on her PhD thesis which addresses how we can improve our support for pupils learning calculation skills.