
Getting into the picture
How a picture is made
When you look at a photograph of a scene, visual cues - such as converging straight lines, shading effects, receding regular patterns and shadows - are processed by your brain to retrieve consistent information about the real scene. Lines parallel to each other in the real scene (such as the tiles on a floor) are imaged as converging lines in the photograph which intersect at a point called the vanishing point. This holds for any set of lines as long as they are parallel to each other in the scene. Two or more aligned vanishing points define a vanishing line, such as the horizon, which defines the eye level of the viewer in the picture.

These visual clues are used by artists in their paintings, in a technique called linear perspective that was invented in the second decade of the fifteenth century in Florence by Filippo Brunelleschi. During the following decade it began to be used by innovative painters as the best way to convey the illusion of a three-dimensional scene on a flat surface. In the seventeenth and eighteenth centuries a number of mathematicians such as Desargues, Pascal, Taylor and Monge became increasingly interested in linear perspective, thus laying the foundations of modern projective geometry. Projective geometry can be regarded as a powerful tool for modelling the rules of linear perspective in a metrical or algebraic framework.
Geometric consistency and measuring heights
We should constantly bear in mind that a painting is a creation that relies upon the artist's and spectator's imaginations to construct a new, artificial world. This world originates from the hands of an artist skilled in achieving effects in which manipulating the perspective may be an advantage and in which accuracy may not be paramount. In particular, before any geometric reconstruction can be applied it is necessary to ascertain the level of geometric accuracy within the painting and, by implication, the desire of its maker for perspectival precision.
There are some simple techniques for assessing the consistency of the painted geometry. Vanishing points and vanishing lines are among the most useful projective entities of an image, and a natural way to assess the correctness of a painting's geometry is to check whether images of parallel lines do intersect in a single point on the painting.
Even in perspectivally constructed images the heights of figures might be varied by the artist according to the status of those represented. For example, the person paying for the painting may be made to appear larger than other figures in the image. Therefore, comparing the heights of people in a painting can prove interesting - not only to ascertain their consistency with perspective rules, but also in order to establish whether any disproportion is an intentional response to hierachies of status.
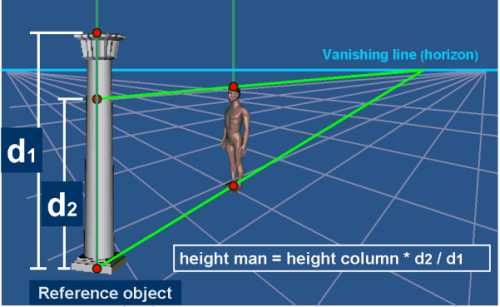
The image above shows how people's heights can be computed directly from perspective images. To compute the height of the man with respect to the height of the column, (or equally to any other reference object chosen from a picture), the height of the man is projected onto the height of the column in the image using the vanishing lines from the top and bottom of the two objects. This gives
$$ \mbox{actual height of man} = \mbox{actual height of column} \times {\rm d}/{\rm d}_1,$$
where d1 and d2 are the measurements from the image of the height of the column and the projected height of the man respectively.
Photographs can behave in a more complicated way, in that the vertical vanishing point may be finite (vertical lines eventually intersect in the image) rather than infinite (as in the example above, where the vertical lines are parallel). In such cases the simple formula above for calculating heights does not work, but instead a slightly more complex formula is used, which includes the finite vertical vanishing point in the calculation.

Comparing heights in the Flagellation.
Step inside the painting by viewing the movie (5M).
Flagellation, by the highly skilled artist and mathematician Piero della Francesca, is one of the most studied paintings from the Italian Renaissance period as it is a masterpiece of perspective technique. The "obsessive" correctness of its geometry makes it a most rewarding painting for detailed mathematical analysis.
The method for computing heights described above can be applied to this painting using the figure of Christ as the reference object. At first glance it is not easy to say whether the heights of the figures in the background are consistent with the ones in the foreground, but this technique shows that the measurements are all quite close to each other, confirming the extreme accuracy and care
for detail for which Piero della Francesca has become noted.

An important application of this theoretical framework is its use in forensic science to measure dimensions of objects and people in images taken by surveillance cameras. The quality of the images is usually very bad (as they are taken by cheap security cameras), and quite often it is not possible to recognize the face of the suspect or distinct features on their clothes. Therefore the height of the person may become an extremely useful identification feature.
In the case of photographs of real objects the reference height (the height of the phone box in the figure on the left) may be known or can be measured in situ and the height of the people in the photo can be computed in absolute terms.
If a painting conforms to the rules of linear perspective then it behaves, geometrically, as a perspective image and it can be treated as analogous to a straightforward photograph of an actual subject.
Deeper into geometry ...
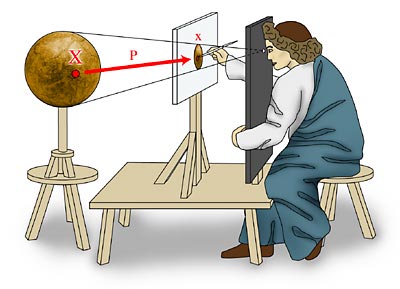
An illustration of Leonardo's perspectograph. A point X on the globe is projected to a point x on the image plane via a straight ray from X to Leonardo's eye.
In a central projection camera model, a three-dimensional point in space is projected onto the image plane by means of straight visual rays from the point in space to the optical centre (such as your eye, see image of Leonardo's "Perspectograph"). This process can be described mathematically by a projection matrix P, which takes a point in three-dimensional space and transforms it into a point on the two-dimensional image plane.
The projection matrix P can be computed from the external and internal camera parameters, such as its position, orientation and focal length.
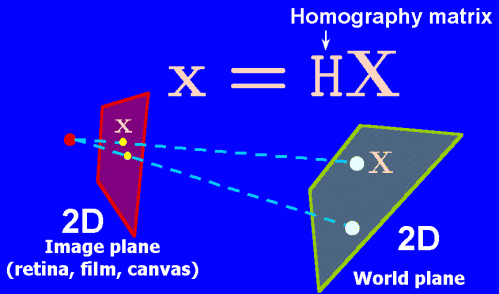
Plane-to-plane homography
In the case where planar surfaces are imaged, the transformation is called a plane-to-plane homography (a simpler matrix H). If the homography between a plane in the scene and the plane of the image (the retina or the canvas) is known, then the image of the planar surface can be rectified into a front-on view.
 Original photo |
 Rectified, front-on view |
The homography can be computed simply by knowing the relative position of four points on the scene plane and their corresponding positions in the image. For example, the left-hand image above is a photograph of a flat wall of a building taken from an angle. Four corners of a window have been selected, and the homography between the plane of the wall and that of the photograph has been computed by mapping the selected four image points to a rectangle with the same aspect ratio as the window. Thanks to the homography, a new view of the wall (on the right) has been generated as if it was looked at from a front-on position.
 A black and white pattern can be seen on the floor in the Flagellation |
 Martin Kemp's manual reconstruction of the floor pattern |
 The computer reconstruction of the floor |
Piero della Francesca's Flagellation shows, on the left hand side, an interesting black and white floor pattern viewed at a angle. Alongside this image is a manually-rectified image of the floor pattern produced by Martin Kemp (in his book "The Science of Art"), and the rectification achieved by applying a homography transformation as described above (where the four vertices of the black and white pattern have been selected as the base points for the computation of the homography, and assumed to be arranged as a perfect square). There is a striking similarity between the computer- and manually-rectified patterns. However, the computer rectification has many advantages, including speed, accuracy and the fact that the rectified image retains the visual characteristics of the original painting. Furthermore, the computer rectification discovers two patterns, one before and one behind the central dark circle on which Christ is standing. The farther instance of the pattern is very difficult to discern by eye in the original painting, while it becomes evident in the rectified view. Another example of Piero della Francesca's incredible skill and precision.
3D reconstructions
Now we get to the exciting bit! If a image has enough geometric consistency, the methods described above (rectifying slanted views, estimating distances from planar surfaces such as heights of people) can quickly produce a complete three-dimensional reconstruction of the image. The three-dimensional reconstruction process can be used to explore the possible structural ambiguities that may arise, and can magnify possible imperfections in the geometry of the painting.
The Trinity
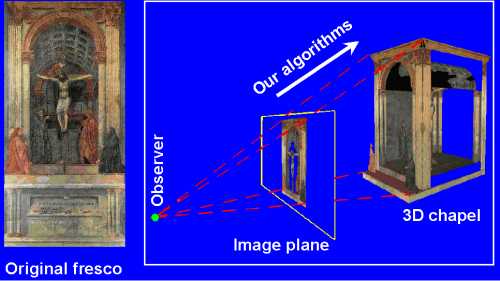
The church of Santa Maria Novella in Florence boasts one of Masaccio's best known frescoes, The Trinity (1426), painted just before his early death in 1428 at the age of 27. The fresco is the first fully-developed perspectival painting from the Renaissance that uses geometry to set up an illusion in relation to the spectator's viewpoint.
The Trinity has been analysed repeatedly using traditional techniques, but no consensus has been achieved. It has become apparent that analyses starting with the assumption that the vault coffers are square result in a different format from those that start with the assumption that the plan of the chapel is square (these two assumptions seem likely, since having a square ground plan seems to be the natural choice from a design point of view, and that of square coffers seems to be more likely from a perceptual point of view), although looking at the painting one may think that the two assumptions are consistent with each other.
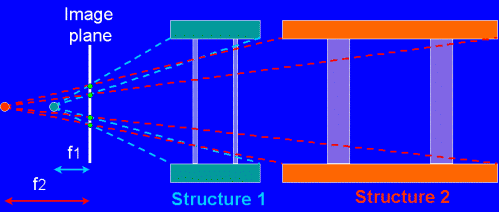
There is an infinite number of reconstructions consistent with the original painting
Single-view reconstruction algorithms have been applied to an electronic image of the fresco to help art historians resolve this debate. Since one image alone is used and no scene metric information is known (the "chapel" is not real), the number of reconstructions consistent with the original painting is infinite. In fact, different choices of the coffers or ground plan aspect ratios yield different consistent three-dimensional models. At this point new questions arise. Which architectonical structure did the artist want to convey? If he had started by laying down a square base, why would he choose rectangular-shaped coffers? Was he aware of the depth ambiguity? Was it done on purpose?
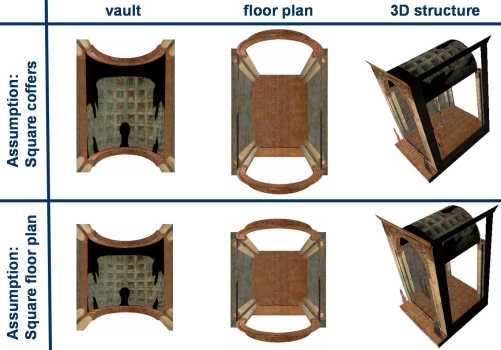
Without exploring the answers in detail here, we suspect that Masaccio began, as most designers would, with the overall shape, and then fitted in the details to look good, and that when he found that his earlier decisions had resulted in coffers that were not quite square (if he noticed!) he decided that they would look effectively square anyway. In the final analysis, visual effect takes over from absolute accuracy.
Whatever the reason for Masaccio's ambiguity, the computer analysis performed here has allowed us to investigate both assumptions rigorously, by building both models efficiently, visualizing them interactively and analysing the shape of vault and base in three dimensions (view the movie for the model with square coffers (5.3M), and the movie for the model with a square base (2M)).
St Jerome in His Study

Step inside the painting by viewing the movie (3.3M).
St Jerome in His Study is an oil painting by the Dutch artist H. Steenwick (1580-1649), who was one of the pioneers of perspectival interiors in Dutch painting. Linear perspective was generally adopted later in northern Europe than in Italy, but it was in Holland, where elaborate depictions of buildings and townscapes in their own right became a major genre for painters in the seventeenth century, that the potential of Brunelleschi's invention for the depiction of actual (or apparently real) views was fully realised.
The accuracy of the perspective in Steenwick's St Jerome, and the amazing management of light and shade as it traverses the spaces, make this painting a very significant early example of Dutch painting of domestic and ecclesiastical interiors, combining in this case both a room and a distant vista into a church. The beautifully characterised passage of the light from the windows on the left, casting shadows across the tiled floor, gives Steenwick's imagined interior an extraordinary sense of veracity.
Given its strong geometrical component (numerous parallel lines and planar surfaces can be observed) the painting proves an ideal input for our reconstruction techniques. Reconstructing this painting in three dimensions also offers the possibility to detect and investigate inconsistencies which are hard to notice through an analysis of the flat original image alone.
 The window as it looks |
 A rectified, front-on |
The images above show the original and a reconstructed front-on view of the large window on the left hand side of the painting. Notice that, while parallelism and angles have been recovered correctly, an unexpected asymmetric curvature of the top arch can be detected - the right side of the arch appears to be thicker than the left side. This inconsistency is made evident by our reconstruction process and is less noticeable in views taken from locations closer to the original view point.
This geometrical imperfection is probably due to the fact that the artist has painted a complicated curve at an angle by eye and without undertaking a precise projection, which probably wasn't visually worth the effort. The inaccuracy in the painting can be interpreted statistically, by assuming that during the painting process there is the same likelihood of the artist making a mistake in any direction and at any point of the canvas. In figure on the left below, the distribution of the uncertainty on the plane of the painting is visualised by superimposing a regular grid of circles on the original painting.
 |
 |
The figure on the right shows a front-on view of the window, computed by the usual method of rectifying the image by applying a homography transformation to the original painting. The circles in the figure on the left are mapped by the reconstruction process into ellipses of increasing size going from left to right, accounting for the reduced accuracy of the right side of the window arch.
The idea of investigating geometric imperfections by generating new views of portions of a painting was already present in what is considered to be the very first treatise on perspective, Della Pictura by Leon Battista Alberti (1435), where he suggested looking at paintings in a mirror to expose any weaknesses. The three-dimensional reconstruction of this image offers another way to expose these weaknesses.
Virtual space, the final frontier...
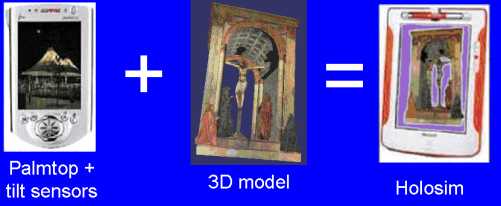
These three-dimensional models can be brought together to create an interactive virtual museum, where viewers can visualise the paintings in three dimensions, and interact with them by "diving" into the virtual scenes. And perhaps the time when we can literally step inside the painting is drawing near. In the first steps towards this goal, researchers from Microsoft have developed the Holosim - a hand-held device, such as a palmtop, fitted with tilt sensors so that as you tip or move the device the three-dimensional simulation on the display responds to your movements - allowing you to observe the object from different view points. This opens up exciting new possibilities such as inspecting a virtual three-dimensional reconstruction of a famous object as we hold it in our hands (own a virtual Ashes trophy), or using it as a window on a virtual space. And for the Trekkies among us, surely the holodeck is only a matter of time.
Acknowledgements
The author would like to thank A. Zisserman, I. Reid, M. Kemp and L. Williams for their collaboration on this work.
About the author

Antonio Criminisi is a researcher at Microsoft Research in Cambridge. His current research interests are in the area of image-based modelling, texture analysis and synthesis, video analysis and editing, 3D reconstruction from single and multiple images with application to Virtual Reality, Forensic Science, Image-Based Rendering and Art History.
Antonio developed the work in this article while he was part of the Visual Geometry Group at the University of Oxford. For more examples of this work and for details of his book, Accurate Visual Metrology from Single and Multiple Uncalibrated Images, you can visit his web page.
Comments
He who knows nothing
It might be interesting to take all known photographs of say, the JFK assassination, and possibly the couple of film clips of the event and apply this rectification technique.
We may extract useful information and discover hitherto unsuspected people or locations to investigate further.