Going up in the world

"Most twining plants are adapted to ascend supports of moderate though of different thicknesses. Our English twiners, as far as I have seen, never twine round trees" - Charles Darwin

You may have noticed, as Darwin did, that while climbing plants can twine around supports of various thicknesses, they tend not to use really thick objects, like trees. You may also have wondered how they are able to hold themselves up despite not being anchored at the top. Mathematicians Alain Goriely of the University of Arizona, USA, and Sébastien Neukirch of the Centre National de la Recherche Scientifique, France, set out to investigate these problems. They discovered that there is a critical thickness of support beyond which plants are unable to climb, and they explained how twining plants hold themselves up.

Goriely and Neukirch modelled their climbing plants as thin elastic rods with their own twist and curvature, winding around a cylindrical support. The mechanics involved in such a set-up is described mathematically by Kirchhoff's theory of elastic rods. To simplify their analysis, the researchers first imagined that the plant only grew in two dimensions, as though it were growing round a horizontal cross-section of the support. A crucial quantity in their model is the plant's natural radius — the radius of the shape in which it would naturally grow were it not for the support getting in the way.

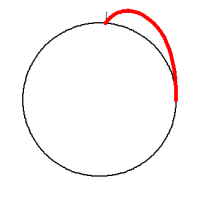
The stem arches away from the support. Image © Sebastien Neukirch.

A climbing plant's natural radius is smaller than the radius of its support. In the two-dimensional model, this means that the plant's curve is tighter than that of the disc it grows around, causing the plant's stem to arch away from the disc. The stem's tip then curves around and re-meets the support. If it does so at a certain place and with a certain angle, then the mechanical forces involved will hold the tip in place and generate tension that is passed along the stem. This tension, the researchers say, is what enable plants to hold themselves up, a problem that had previously baffled botanists.

As the plant grows, the tip moves along the stem, always finding the right position to uphold the necessary tension. The model showed that the thicker the support, the harder the tip has to push into the support to maintain its grip. This means that the angle between the stem at its tip and the tangent to the support has to become larger as the thickness of the stem increases. Once a critical thickness is reached, the angle is required to be so large that the tip loses its grip on the support and starts curling in on itself. The critical thickness, according to the model, is 3.3 times the natural radius of the plant.

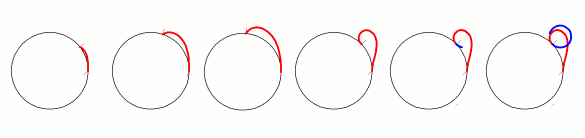
If the support is too thick, the angle between the stem of the plant and the tangent to the support becomes too large and the plant curls back on itself. Image © Sebastien Neukirch.

This implies that particularly thick trees may hope to stay free of annoying climbers, however there is a caveat. The more friction there is between the tree and the climber, the easier it is for the climber to maintain its grip. After introducing the effects of friction into their model, the researchers found that the critical thickness can increase to up to eight times the natural radius of the plant.

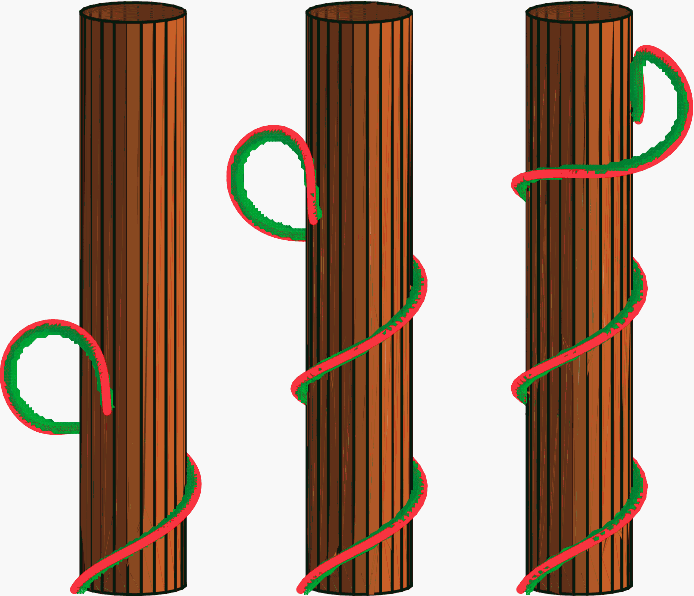
Image © Alain Goriely.

When Goriely and Neukirch generalised their model to take account of the fact that plants grow in three dimensions (that they grow up, as well as round and round), they discovered that, while the calculations were somewhat more difficult, the main results still held — the plant generates the necessary tension by arching away from the support and the critical thickness stayed in the region of 3.3 times its natural radius. However, they had to leave some simplifications in their model. For example, they did not consider the possibility that a plant's natural shape might be distorted by being stretched, twisted, etc., choosing instead to leave this for future work.

As a result of this work, we now know that Darwin was mostly correct — we would not expect to see plants twining around massive trees, since they are usually above the critical thickness. However, it is of course possible that some plants could have a large enough natural radius that a tree was below this critical value, and it would thus be able to entwine around it.

Further Reading

• The original paper was published in Physical Review Letters.
• Alain Goriely's website, with links to his work on vines.
• To find out more about highly interesting applications of the theory of elastic rods, read Plus article Spaghetti breakthrough.