
How do we remember? And how quickly do we forget?
Do you and your friends have a favourite album or song on repeat? Is everyone raving about a new movie? Is a research paper causing a buzz in your field? The question of how something rises to the top and then drifts out of our collective consciousness has intrigued social sciencists and psychologists. Now researchers from maths, physics and economics have used big data to show that the fates of our collective memories, whether of a song, a research paper, an invention or a sports star, are all described by the same mathematical equation.
A collective memory is something that is remembered by a group of people – from your family's recollection of your hilarious antics as a child to a nation's memory of an important person, event or cultural product. Such memories are created and maintained in the group’s memory by two processes: people talking about it (called communicative memory) and people physically recording the information (cultural memory).

The prominence of something in our collective memory can be observed through the attention we give, such as through online searches. (Image is "Digital Montage Number 2", floppy disk painting by Nick Gentry, CC BY-SA 3.0)
One way to observe the prominence of something in our collective memory is to measure how much attention we pay to it. Today, if we're talking about something we're probably going to be prompted to look it up online. Researcher Christian Candia and colleagues from USA and Chile captured this online attention by the number of page views of wikipedia entries (they focused on the biographies of high performing athletes), the play count of movie trailers on youtube and the popularity of songs on a streaming service. For research papers and patents the researchers used citation counts to measure how much attention they received.
The availability of these datasets, part of the phenomenon known as big data, allowed the researchers to test their hypotheses for how cultural products rise and fade away in our collective memories. This data, such as how many page views the biography of an olympic athlete has received, doesn't directly measure how strong a collective memory is. Instead the researchers describe it as a measure of the "spillovers of attentions that result in online searchers or references".
Over time the attention something receives, as measured in this data, drops off. This represents the decay in communicative memory: people are more likely to look things up in response to conversation. But it also represents a decay in cultural memory: the total cultural memory (made up of recorded information) is always increasing, so the proportion of the cultural memory that one product (song, movie, biography, paper) represents is always decreasing.
Previously, the decay of collective memories had been modelled mathematically with exponential functions. But in this work the researchers used something called a biexponential function, a sum of two exponential functions, which decays at a very fast rate for a period, then switches to decaying at a slower rate.
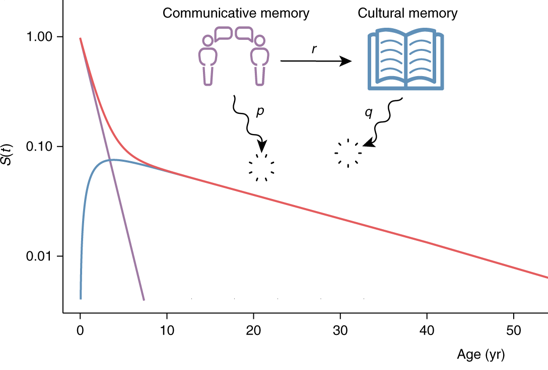
The red biexponential function is the sum of two exponential functions, the purple curve of the decay of communicative memory, and the blue curve of the decay of cultural memory.
The contribution of two different exponential functions comes from the researchers assuming that the total attention a cultural product received at any one time, $S(t)$, was the sum of the attention it gets through both communicative, $u(t)$, and cultural, $v(t)$, memory: $$ S(t) = u(t) + v(t) $$ They predicted that communicative memory decayed exponentially with rate $p+r$, where $r$ described the movement of the information from communicative to cultural memory as the memory was recorded. The proportion a cultural product represents of the total cultural memory decayed exponentially at the much slower rate $q$. The change in the attention from communicative memory, $u(t)$, and cultural memory, $v(t)$, from one time step to the next ($t$ to $t+1$) can be thought of as: $$ u(t+1)=(1-p)\times u(t)-r\times u(t) $$ $$ v(t+1)=(1-q)\times v(t)+r\times u(t). $$ These can be transformed into differential equations and solved for the initial conditions (ie, when $t=0$) of the initial communicative memory set to be some value $N$, and that at the beginning of the process there is no cultural memory. This gives the biexponential function $$ S(t)=\frac{N}{p+r-q} ( (p-q)e^{-(p+r)t} +re^{-qt}) $$ describing the decay of a cultural product in our collective memory: it quickly fades from our communicative memory as we stop talking about it (the first phase of the function), and then more gradually fades from our cultural memory.
Candia and colleagues tested this model against the various datasets and found that it fitted much more closely than previous mathematical models. While the parameters are different for different cultural products, the decay of the observed attention has the same shape described by the biexponential function. People seem to stop talking about songs, movies, papers and patents after around 5-10 years, whereas people keep talking about athletes for much longer, for around 15-30 years.
This new approach of using big data opens up the possibility of testing this model of collective memory further to see whether the collective memories of, say, events, also follow the same pattern. It might also suggest ways of how to keep things in our collective memory for longer. But for now, it's clear that if you wish to remain the talk of the town, be good at sport rather than a one-hit wonder.