
How long a line can a pencil draw?
When did the backs of envelopes first became a popular place for jotting rough-and-ready calculations? Was it before or after people started to use the "back of a fag packet", or in the USA, the back of a napkin?
Regardless of where the expression was first coined, the back of an envelope has come to symbolise any sort of rough-and-ready type of calculation that gives an indication of what the right answer will be.
It is the tool that people in business use for quickly checking the viability of a new project. Engineers use it to check if a proposed solution is likely to work. And commentators on statistics use it to help make sense of the myriad numbers that are thrown out by politicians, "expert" pundits and marketers.
But some back-of-envelope calculations are done just for the fun of it — an intellectual exercise in working out approximate answers without access to much data.
Here's just one whimsical example. How long a line can a pencil draw?

This article is an extract from the book Maths on the back of an envelope by Rob Eastaway.
In 2007, Discover magazine claimed that a regular pencil can write 45,000 words and draw a line 35 miles long. These two claims have been repeated many times since, including by the BBC's respected source of trivia QI. But are they true?
Soon after the Discover article was published, Keith Eldred of Pennsylvania (or should it be Pencil-vania) set out to test the 45,000-word claim in a project called To write a mockingbird. Eldred recruited a team of 26 people to work as a tag team copying out the whole of Harper Lee's classic novel using a single standard yellow pencil (the equivalent of a British HB pencil).
It took the group more than 100 hours to write out the entire book, and at the end of it they counted 100,388 words. They still had a stub of pencil 1.25 inches long, so in theory they could maybe have written another 20,000 words. It was convincing proof that a pencil is capable of writing well over 45,000 words. However, the project team used their pencil beyond typical practical length, and were overly careful not to waste too much lead when sharpening, so for practical purposes the claim that a typical pencil can write 45,000 words seems reasonable.
The 35-mile claim, however, seems more dubious. Here's one way to challenge it.
Let's say a pencil can write 50,000 words. How much "line" is there in a word? We need to know the average word length. Touch typists measure typing speed on the basis of words being 5 characters long, which seems a reasonable figure to use. But how "long" is a character? Using a short ruler, I measured that I use 5–10 mm of pencil line per letter. Let's call it 8 mm per letter, so the average word is equivalent to a line of length:
5 × 8= 40 mm = 0.04 metres
50,000 words × 0.04 metres = 2,000 metres, which is a bit over a mile. Even if we can eke out 100,000 words to get 2 miles, it looks like the claim of 35 miles is out by an order of magnitude.
Is there any way to get a pencil to draw a line 35 miles long?
One tactic that will help a pencil to last longer is to press less hard. You'll also use less lead if the pencil is sharp (because the line is narrower) but there's a problem with this: sharpening a pencil wastes a surprising amount of lead. As the diagram below shows, the sharpening process trims a cylinder into a cone, and some school maths to compare the volume of the two shapes shows that at least two-thirds of the lead is chucked in the bin when it is sharpened. In reality the amount of waste is probably nearer to 90%.
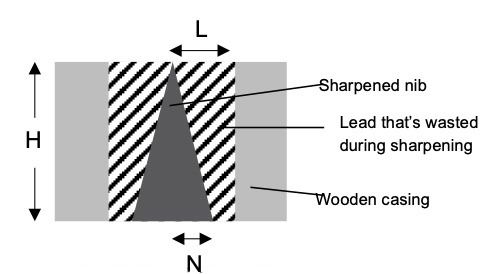
The amount of pencil wasted is the volume of the cylinder of lead (which is $\pi L^2 H$) minus the volume of the sharpened conical nib (which is $1/3 \pi N^2 H$). Even if $N=L$, two thirds of the lead is wasted.
So if you want to be more efficient with a pencil, you need a sharpener that trims off as little lead as possible. Better still, use a propelling pencil, which doesn't need sharpening at all. Will it draw a line of 35 miles? Almost certainly not. But it might at least get your mileage into double figures.
About this article

This article is an extract from the book Maths on the back of an envelope by Rob Eastaway.
Rob Eastaway is an author and speaker whose books on the maths of everyday life include How many socks make a pair? and The hidden maths of sport (with John Haigh). He is the Director of Maths Inspiration, a national programme of interactive lecture shows in theatres that has reached over 150,000 teenagers in the last ten years.