
I'm not paying that!
Since the first plane took paying passengers in the 1920s, airlines have been trying hard to make as much money as possible out of the travelling public. Doing away with the silver service on flights might have saved them a few pennies, but using mathematical principles to decide how to price their tickets has certainly made them a lot of money.
Revenue Management
Airlines began by charging a single price for identical seats on their aircraft but, in the 1970s, realised that if they sold a few seats early at a discounted rate (an early bird value price), and with more restrictive conditions, then they could fill up some of the seats that would otherwise not have been sold. But how many seats should they sell at the discounted price? Sell too many and they would not have enough seats left for the higher paying customers. Too few and they would still be left with empty seats on take-off. This is the heart of the revenue management problem: what price should an airline charge for each of the seats on its flights so that it maximises its revenue (i.e. the total money coming in from ticket sales). Put another way, how many seats should an airline reserve for the high-paying customers and how many can it sell at bucket-shop prices?

Knowing the customer
Each potential customer will have what is called a reserve price for a flight ticket, which might vary with the time left before the flight and will also depend on the passenger's reason for travelling. A customer's reserve price is the maximum that they would pay to make the trip. Customers don't tell airlines what their reserve price for a flight is (assuming that they know it themselves), so a lot of the analysis that airlines do involves trying to work out the distribution of reserve prices for their potential customers. Why is this knowledge so important? Every time an airline sells a ticket to a customer at a price below their reserve price, the airline is losing potential revenue because the customer would have paid more for it. The airline also loses potential revenue if it underestimates the number of people prepared to pay higher fares and sells too many tickets at a discounted rate. The distribution of reserve prices tells an airline how many people would want to buy a ticket at any given fare. If it knew exactly what this was, it would always have seats remaining for the high-paying customers.

Money: maximise it!
Estimating what customers are prepared to pay involves a thorough analysis of sales data from previous flights. Airlines will look for trends in the numbers of passengers: a general increase or decrease in numbers. They will also look for cycles in the data. These might just be weekly cycles (busy flights on Monday and Friday, empty flights on a Tuesday lunchtime or 6am on a Sunday) but there will also be annual cycles, especially on holiday flights. In fact, forecasts need to take into account everything from school holidays and big football matches to terrorist activity and high fuel prices - anything that could affect people's desire to travel. This is why there will always be a need for the human factor in forecasting.
Maximising the revenue
Even when an airline has a good idea of the distribution of reserve prices for its potential customers, deciding what to charge for each of the seats will mean performing a complex constrained optimisation problem. The problem is constrained because the aircraft only has a limited capacity. We can consider a very simplified example to demonstrate the kind of problem that airlines face.Let's assume that we have just two fare classes on our aeroplane and that we have good estimates of the expected demands for the two ticket types. For the moment, we'll assume that our demand is deterministic, i.e. it isn't random, so we can predict it exactly. With these assumptions, we can write the revenue management problem as a series of linear equations.
We wish to maximise the expected revenue generated by the flight. For the two-fares example, the expected revenue is $$ y = p_lx_l + p_hx_h$$ where we expect to sell $x_l$ low-cost tickets at the discount price of $p_l$ and $x_h$ high-cost tickets at the higher price of $p_h$. We also have certain constraints that $x_l$ and $x_h$ must obey:
- We cannot sell more tickets than we have seats on the plane (actually airlines do sometimes ignore this constraint — a technique called overbooking — which we'll discuss below), therefore, $x_l + x_h \leq C$, where $C$ is the number of seats on the aircraft.
- The number of low-cost seats sold must be less than or equal to the demand for low-cost seats: $x_l \leq d_l.$
- The number of high-cost seats sold must be less than or equal to the demand for high-cost seats: $x_h \leq d_h$.
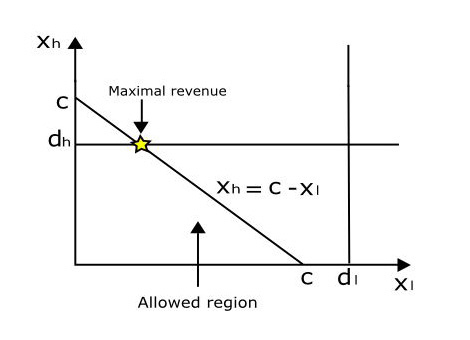
So, we can see from the diagram that to maximise the revenue, we should set $x_h$ such that we satisfy all of the high-fare paying customers and we should fill up the remaining seats with passengers paying discounted fares.
Adding complexity
In reality, the airline not only has to decide on the optimal allocation of seats to fare classes but it also must decide what will be the best fares to charge in each of those classes. The optimisation is said to be stochastic, because some of the variables in the problem are random. In this case, the numbers of people wanting to buy tickets at a given fare are random variables. The fact that the problem is stochastic means that the airline needs to work with expected values and probability distributions, which makes the optimisation harder to solve.

Complexity in numbers
Airlines still use linear programming to solve these stochastic optimisation problems, but use different decision variables from those in the simple example considered above. Rather than deciding on the number of seats to sell at a given fare, an airline considers each seat in turn and decides whether or not to sell it at a given rate. Therefore, for an aircraft with 100 seats and 2 fare classes, there would be 200 decision variables. The decision variables can only take on the values 1 (sell the seat at this fare) or 0 (don't sell the seat at this fare). Because of this, a specialised form of linear programming called integer programming must be used to solve the problem. Integer programs take longer to solve, so the airlines need a lot of computing power.
Another method used by airlines to decide whether or not to sell a ticket is an opportunity cost. An opportunity cost is defined to be the cost of giving up the next best option when making a decision. Thinking about the early-bird discounts discussed above, the opportunity cost of selling the ticket at a discount is the expected cost of giving up the opportunity of perhaps selling the ticket later at a higher price. Each time the airline receives a request for a discounted ticket, it weighs up the revenue that it knows it will receive by selling the ticket now at a low price against the expected revenue that it would receive if it reserved the ticket for a higher paying passenger. The expected revenue from the higher-paying passenger is equal to the probability that they will request a ticket on the flight multiplied by the higher fare and so using the expected revenue takes into account the fact that a higher paying passenger may or may not request a ticket later in the selling period.
As airlines have become more sophisticated, the number of different prices that they charge for tickets has increased and today there are often around ten different fare classes for economy passengers. Each of the fare classes will have slightly different conditions associated with it. The purpose of these conditions is usually simply to make the lower fares unattractive to passengers prepared to pay more. For example, the cheapest fares might insist that the ticket is a return with the passenger being away over a Saturday night (deterring business people from buying them) and the most expensive will be fully flexible tickets. The airline must now decide on prices for each of the different fare classes and the number of seats to reserve for the different classes, which complicates the problem further as it introduces more variables. The higher the number of variables the longer the optimisation algorithms will take to run.
Overbooking

Want a holiday? Hop on a plane!
Occasionally people don't show up for a flight that they've booked. They might miss the train that was going to take them to the airport, have been in a business meeting that over ran or simply have changed their mind about the flight and decided not to go at all. Because of this, airlines often sell more tickets on a flight than there are seats, a practice known as overbooking. They are taking a gamble that some of the people won't show up at the check-in desk. Obviously, if all of the passengers do turn up, then the airline has an additional cost to pay as customers have every right to some compensation for being bumped off their flight. In fact, some people actually deliberately book themselves on busy flights in an attempt to get the compensation money, which can be more than the cost of the ticket!
Overbooking was the first area to receive the "mathematical treatment", and to begin with airlines tried to sell just enough extra seats so that the probability of bumping a passenger off a flight was between acceptable bounds. These days, the effects of overbooking are included in the revenue maximisation problem, using the probability distributions describing passengers' behaviour to estimate the expected costs and/or benefits of issuing more tickets than seats.
No frills airlines

No frills
Increased complexity
An average of 1250 flights operate through Heathrow every day. Multiply that by the number of major airports in the world and you have a very complex network of interconnecting routes. As the network has become more complicated, so too has the revenue management problem. First, you have the impact of competition on your demand estimates. For example, BA may estimate the number of passengers that will buy tickets in a particular class on a particular flight only to find that KLM has decided to sell its tickets on the same route at a much lower price. The next complication is multi-leg flights. In the USA in particular, it is rare to have point-to-point connections between cities. Instead, airlines generally use what is known as a "hub-and-spoke" system, whereby passengers will first connect to a hub, before boarding another flight to take them on to their destination. This makes the demand for individual flights much harder to forecast, as the people travelling on the flights might be making very different journeys. The need to optimise fares over several different combinations of flights also complicates the revenue maximisation problem considerably.
Not just airlines
It isn't only airlines who benefit from a mathematical approach to pricing their products. The ideas discussed above are also used to price rental cars, hotel rooms, cinema tickets, airport parking and tee times on golf courses. Even the sale of turkeys at Christmas can be optimised using the no-frills airline revenue management model. In fact, the sale of any set of identical products with an expiry date and limited capacity could be optimised using revenue management. Revenue management is part of Operational Research, an area of mathematics that investigates the solution of real-world business and organisational problems. If you would like to find out more about Operational Research, take a look at the Operational Research Society's webpage.
About the author

Christine Currie is a lecturer in Operational Research in the School of Mathematics at the University of Southampton. Her research includes modelling diseases as well as pricing airline tickets. She spends most of her spare time running around the countryside and orienteering.