Influenza virus: it's all in the packaging!
Back to the Unravelling genetic secrets package
Back to the Do you know what's good for you package
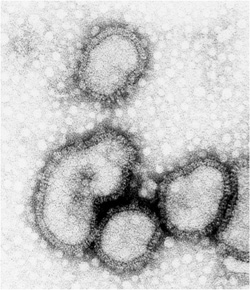
A real influenza virion [Image courtesy Edward Hutchinson]
Influenza is a seasonal disease we are all familiar with. Most of us have experienced the misery of being cooped up in bed with a streaming nose, aching joints and temperature now and again. However sometimes influenza can cause serious complications, particularly in the elderly, occasionally leading to death. And this year's swine flu pandemic, thankfully with fewer deaths than expected, has given us an inkling of just how dangerous influenza could be.
Influenza comes in three types — A, B and C — with A the most common and the cause of the major outbreaks. A virus particle, called a virion, is a roughly spherical shell containing the influenza genome, and covered by two types of surface proteins called antigens: one (H) which allows the virus to enter host cells, and the other (N) which allows new virions to be released from infected host cells. Influenza A can be characterised into different strains according to its surface antigens, such as the now familiar swine flu or H1N1 virus, and the H5N1 bird flu that emerged in the 1990s in Asia.

The virion has a spherical(ish) shell covered with surface proteins, and inside the genome is made up of 8 RNA segments
What makes influenza so dangerous is the way in which it evolves. All viruses evolve, with minor genetic mutations either being carried forward to new generations or dying out. This normal form of evolution in a virus is called antigenic drift, where the influenza slowly changes over time, and we retain some partial immunity to the evolved virus thanks to our immune systems remembering past infections. However, things become very dangerous when antigenic shift occurs. In this case two different strains of influenza mix together to create what is essentially a new disease to which we have no immunity.
During influenza infection, viruses spread from cell to cell, hijacking cellular machinery to make more copies of themselves. The influenza genome is unusual in being made of several segments, like mini chromosomes, rather than one continuous genome. The different segments are replicated separately, but must end up together inside a new virus particle, which then buds off from the cell surface. There are eight segments for influenza A, and all contain important genes, so a virus needs a full set of segments to be fully viable.
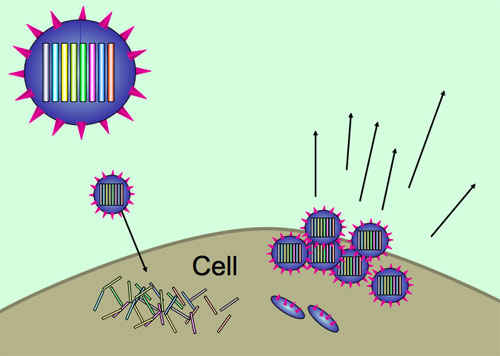
Viruses use host cells to replicate themselves, with each new virion containing all eight segments of the influenza genome.
And now we are in the midst of H1N1 pandemic, which despite its quick spread around the globe has been fatal in far fewer cases than originally predicted. This swine flu is a result of several stages of reassortment, possibly existing in its current form for some years. Reassortment was implicated in generating at least two of the three pandemic strains in the 20th century (the evidence for the 1918 pandemic is unclear and an interesting current topic). Understanding packaging is key to understanding reassortment.
Let me count the ways...
There was debate in the past about whether influenza packages segments at random or whether there is a special mechanism to ensure each virus particle gets the eight different segments. As a mathematician, I always found this uncertainty slightly puzzling, as the numbers immediately suggest random packaging would be a truly pathetic strategy for a virus! If we number the segments 1 to 8, then random packaging is equivalent to picking eight numbers at random from this set, say {5, 5, 7, 4, 1, 6, 3, 8}. But this example won't do, as it doesn't contain all eight segments. There are 88 = 16,777,216 ways of picking a random set of eight numbers, with all of these random sets equally likely to be picked. But the number of ways of picking exactly one of each of the segments is
8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 8! = 40,320.
So the chances of picking a complete set at random is 8!/88 = 0.0024, or less than 1 in 400.

How many do I have to eat to get a full set of toys? All in the name of science! [Image courtesy of Dr Andrew Conlan]
So is random packaging any good? No, because less than 1 in 400 virions will be viable. It is clear that influenza could do much better by being a bit less random, or by evolving to package more segments. The success of this random strategy is similar to asking how many Kinder Eggs I'd have to eat in order to get a full set of toys (which I have explored experimentally)!
So what about packing more than eight segments into each virion? Then we could continue to pick segments at random until we have all eight: say {5, 5, 7, 4, 1, 6, 3, 2, 4, 1, 5, 8}. But how many segments do we expect to need before we have all eight?
On the first choice, all eight of the eight possible segments would give us our first distinct segment, so we only need to choose 8/8 = 1 for one distinct segment. Now we have one segment, only seven of the eight possible segments are different, so on average we would need to choose another 8/7 segments to get a second distinct segment in our virion. For the third distinct segment, six of the eight possibilities would do, so we would need to pick another 8/6 segments... and so on. So, on average, we expect to need to choose
8/8 + 8/7 + 8/6 + 8/5 + 8/4 + 8/3 + 8/2 + 8/1 = 21.7,
Mathematics can be more fussy!
We now know that influenza doesn't get around the packaging problem by simply grabbing more segments. Current experimental evidence suggests that segments are packaged specifically: the virus has some way to ensure that it usually has exactly one of each segment. We don't yet know exactly how this happens, but for packaging to be specific, it follows that there must be something about each of the eight segments that acts to distinguish it from the others. It is possible that these labels, or packaging signals, work by interacting with each other in some way. By extensive experiments, labs around the world have started to identify where in the influenza genome these packaging signals might be for some of the segments. These searching experiments are costly and time-consuming if one must search everywhere in the genome, and they might not pinpoint signals in detail, so this is an ideal place for mathematics to help.
We are taking a joint approach between mathematicians and virologists at the University of Cambridge to find and understand these packaging signals. We collaborate with Dr Paul Digard and his lab, who are based in the Department of Pathology. We hope that by combining biological knowledge and insight with a mathematical approach we might be able to pin down in some detail the likely locations of these packaging signals. Theory alone isn't enough: we can follow up our computational work with experiments to explore these likely locations for the packaging signals, for example by making mutant viruses through reverse genetics.
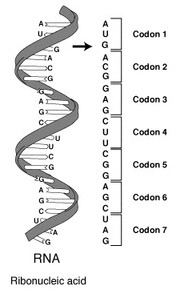
An RNA strand: the codons (the nucleotide triples) specify amino acids
The influenza virus genome is made up of 8 segments of RNA which vary from 890 to 2341 nucleotides in length. Nucleotides — adenine (A), uracil (U), guanine (G) and cytosine (C)— are the molecules that make up the strand of RNA. The RNA strand is read as sequence of nucleotide triples (called codons): each codon defines an amino acid, and the sequence of amino acids the RNA specifies builds up a particular protein molecule. (You can read an excellent introduction to genetics at the Virtual Genetics Education Centre.)
Our computational methods make use of the large amount of influenza genome sequences publicly available (such as those from the Influenza Virus Resource). The packaging signals appear to be embedded in regions of the genome that encode proteins, like a message hidden within another message. To find them, we make use of redundancy in the genetic code to try to spot the regions where there is an apparently inexplicable constraint on the genome. There are many possible sequences that encode the same protein, and the virus ought to be able to mutate to any of these synonymous sequences. But in parts of each segment of the virus, the genome sequence does not vary despite many variations being possible.
To find the suspicious regions of the genome segments, we align hundreds of examples of the genome sequence. For example the following sequences are all from the segment 1 of the influenza virus:
| auggaGagaauaaaAgaacuaAgA... |
| auggaAagaauaaaAgaacuaCgG... |
| auggaAagaauaaaAgaacuaCgG... |
| auggaAagaauaaaAgaacuaAgA... |
| auggaGagaauaaaGgaacuaAgA... |
These break down into codons as follows:
aug gaG aga aua aaA gaa cua AgA...
aug gaA aga aua aaA gaa cua CgG...
aug gaA aga aua aaA gaa cua CgG...
aug gaA aga aua aaA gaa cua AgA...
aug gaG aga aua aaG gaa cua AgA...
Despite slight differences in the sequences (in the capitalised positions), all these sequences encode the same series of amino acids:
Met Glu Arg Ile Lys Glu Leu Arg...
All the sequences must start with Methionine (Met), encoded aug, as this codon is used to indicate the start of the reading frame. This codon can't tell us anything about packaging signals.
The next codon is Glutamic acid (Glu), which can be encoded either as gag or gaa (see the RNA codon table). As both of these variations are present in the genome sequence, this codon is unlikely to be part of the packaging signal.
The third codon is Arginine (Arg). There are six possible ways of encoding Arginine: cgt,cgc,cga,cgg, agg as well as aga. However as there is no variation in this codon for these sequences, so we would suspect this region might act as a packaging signal.
In fact, we can come up with a score for every position in the sequence (based on the number of variations possible, as well as some other factors, such as codon bias) where low scores mean there's suspiciously little variation, when variation would have been possible:
aug gag aga…
aug gaa aga…
1.00 1.00 0.01...
...but why do we care?
Once we have pin-pointed suspicious regions in the genome, the Digard laboratory can explore them by engineering mutant viruses to see if the packaging process is broken by changes in those locations in the genome. The results we have are promising, and it seems that our methods are identifying regions of interest, but there is so much more we want to do.
There are ways we can improve our methods to make better use of the increasing numbers of full genomes of influenza available. (This is currently being researched by a PhD student in my group, Johann von Kirchbach). Also, if we can find any covariances between signals (e.g. when one site on the genome mutated, another site elsewhere usually also mutated), we might be able to begin uncovering clues as to how these signals work: this would be an important step. Then we hope to formulate new experiments to explore further.
Understanding the packaging process of influenza and uncovering the packaging signals that drive it would be a major step in understanding how viruses work. Not only is this of basic virological interest, could also lead to possible treatments. And importantly, as we make our way through the first flu pandemic in half a century, this would lead to a better understanding of the reassortment of "normal" flu with avian or swine flu, that allow dangerous viruses to become adept at infecting human. Perhaps this research will give us another defense against pandemics in the future.Back to the Mathematics of infectious disease package and the Unravelling genetic secrets package
About this article

Julia Gog is Lecturer in Applied Mathematics at the University of Cambridge. Julia and her research group use mathematics and computers to help understand the dynamics of infectious diseases, particularly influenza. She studied mathematics first at university, and then moved towards biology for her PhD on disease modelling. Her research now has links with the Departments of Zoology and Virology, the Vet School and of course the Department of Applied Mathematics and Theoretical Physics. Julia is a Royal Society University Research Fellow and also a fellow of Queens’ College.