Avi Wigderson (Photo: Cliff Moore/Institute for Advanced Study, Princeton, NJ USA/AbelPrize)

You are faced with a difficult problem, it is not easily solved. How do you feel? Well, if you are Avi Wigderson, one of the winners of the 2021 Abel Prize, you are very happy! Difficult problems have given him a lifelong feast of mathematics to enjoy.

Wigderson has spent his life working on understanding how hard problems are for computers to solve, an area called complexity theory. He has been recognised for his contribution to widening and deepening the theory of computational complexity, a contribution that is arguably greater than that of any single other person.

And we should all be as happy about hard problems as Wigderson, because they have enabled the modern world. Our digital lives are all built on modern cryptography which, he said, is "based on the idea of what is hiding the secret is the computational difficulty of a problem." The difficult problem in this case is to do with prime numbers: factoring a very large number into a product of two prime numbers. (You can read more about cryptography in Safety in numbers.)

This factoring problem is a perfect example of the kind of hard problems at the heart of complexity theory. Suppose you are given a very large number, say,

1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139.

And then you are told that the factors of this number are

37975227936943673922808872755445627854565536638199

and

40094690950920881030683735292761468389214899724061.

It is very easy to check if this is the correct solution: you just need to use the standard multiplication methods you learnt in school. For a computer this is a very quick task, and falls into the category of polynomial time in complexity theory: the number of steps a computer would take to do this multiplication is proportional to some power of the size of the numbers involved. But factoring a number is a much more difficult job, and we currently have no algorithms that can factor a number in polynomial time.

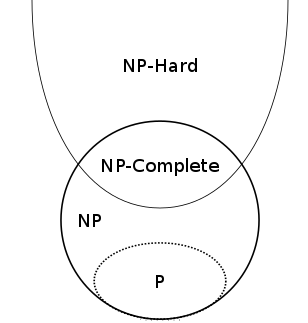
The hierarchy of complexity (assuming the NP class is not equal to the P class). Image: Behnam Esfahbod, CC BY-SA 3.0.

This puts factoring in the class of NP (standing for nondeterministic polynomial time) – those problems that seem hard to solve, but if you have a solution it is easy to check (that is, a computer can do it in polynomial time) that this solution is correct. You can think of them as one-way problems – hard to solve but easy to check. (You can read more about the different classes of complexity in What's your problem?, and you can see evidence of how hard it can be to factor numbers in the RSA challenge.)

One of the most important open problems in mathematics is whether these two classes of problems, P and NP, are the same? Are the problems in NP really as hard to solve as we think, or is it just that nobody has found fast solutions yet? Wigderson, as with most mathematicians, believes that P ≠ NP, and that there are some problems that are truly hard. "It's a wonderful axiom, that some problems are difficult," Wigderson said. "It seems to hold in real life, and suddenly you can do these wonderful things."

Zero knowledge proofs

One of the first wonderful things that Wigderson did with hard problems happened during his postdoctoral research, which he said was like playing amazing games: "Can you do this impossible task? Can we exchange secrets? Is it possible to prove theorems without providing absolutely any detail about the proof, except that your proof is correct?"

It was this last impossible question that was to be his first significant contribution to the field: zero knowledge proofs. "This appears to be the antithesis of mathematics," Wigderson said. Mathematicians not only want a proof of a theorem that they know to be correct, but they also want to understand what is going on: "The proof should be revealing." But on the other hand, in cryptography you often want to be able to prove something to someone else, but you do not want to reveal the details of why it is true. You want to be able to prove that the number used in your encryption is a product of two prime numbers, but you are not willing to reveal which two.

When he was a postdoctoral researcher, Wigderson, together with Oded Goldreich and Silvio Micali, proved that this new concept of zero-knowledge proofs can be used to prove, in secret, any public result about secret data. (You can read more details about zero-knowledge proofs and their role in cryptography in these lovely notes of Wigderson's lecture, taken by Dai Tri Man Lê) Now, more than 30 years later, zero-knowledge proofs are being used in blockchain technology.

The power of randomness, and the power of removing randomness

"It's good to have hard problems," said Wigderson. The things you can do with them are "amazing, shocking and surprising. But there's other benefits of hard problems – with them you can build pseudorandom number generators."

The power of randomness has long fascinated Wigderson. Mathematicians have been able to come up with algorithms that do many tasks. But for many problems you hit a brick wall unless these algorithms use the power of randomness. This means that rather than being deterministic (explicitly setting out what happens), some random input is also required. For example, some of the probabilistic algorithms that test if a number is prime rely on repeatedly doing mathematical checks for randomly selected numbers against the potentially prime number. The more randomly chosen numbers you successfully check against, the more you can be sure that your number really is prime. There is a deterministic algorithm for checking if a number is prime, but the random prime testing algorithms are much, much quicker. So in some cases random algorithms are used today because they are more efficient. And for some problems, no deterministic algorithm is known.

"The real theoretical question is, is it just that we are too stupid to find a deterministic algorithm?" Wigderson said. One important reason why it might be important to have a deterministic algorithm is that there is always a small chance of producing the wrong answer with a probabilistic algorithm. For example, although we have a deterministic algorithm for checking if a number is prime, this is far less efficient that the probabilistic algorithms. But if you are relying on your numbers definitely being prime in order to ensure the security of your cryptography system, you might want to be sure and use the deterministic algorithm.

Can we always eliminate randomness from algorithms? Wigderson collaborated with many researchers to show that we can be almost certain we can, as long as an assumption that is very similar to P ≠ NP is true. This assumption is a slightly stronger statement: that not only are there problems in NP that are not in P (that is, they are not solvable in polynomial time), but also that there are some NP problems that are exponentially hard. (You can read more details in Wigderson’s lecture notes, taken by Dai Tri Man Lê.)

If this stronger statement is true, Wigderson, together with László Babai, Lance Fortnow, Noam Nisan and Russell Impagliazzo, proved that you can always replace the random input required by your random algorithm with a pseudorandom input. First, you allow yourself a few truly random numbers to act as a seed. Then, if you have a one-way maths operation (that’s easy to do in one direction but hard to do in the other), you can apply your one-way operation to your random seeds and return a new number, and you can then append that new number to your existing sequence. Repeating this process of applying your one-way operation to the later numbers in your sequence, continues to generate new numbers. The result is a pseudorandom sequence, which is built according to explicit instructions (deterministically) from the initial random number seeds. What’s more, this pseudorandom sequence is then very hard to distinguish from a truly random one: in order to untangle its deterministic construction you’d have to be able to quickly solve the very hard problem of reversing your one-way maths operation.

Wigderson explained: "We know roughly the following: the assumption that is very similar to P versus NP, that some problems are exponentially hard, if that holds, then you can replace every probabilistic algorithm with a determinist one. You can eliminate randomness always – so hard problems are useful in a very different way!"

Wigderson has spent his life tackling hard problems. His career started in the infancy of complexity theory, and he now finds himself working in an area that is important in both computer science and mathematics. He was recognised for his contributions to computer science in 1994 with the Rolf Nevanlinna Prize, and today for his contributions to mathematics with the Abel Prize. "I consider myself unbelievably lucky to live in this age," he says. "[Computational complexity] is a young field. It is a very democratic field. It is a very friendly field, it is a field that is very collaborative, that suits my nature. And definitely, it is bursting with intellectual problems and challenges. It is a very fantastic existence!"

All quotes have been taken from the lovely video portrait of Avi Wigderson, produced by the Heidelberg Laureate Forum in 2019, which you can watch below.