
Light's identity crisis
A moving charged particle, such as an electron, experiences electric and magnetic forces. In the middle of the 19th century, the Scottish physicist James Clerk Maxwell wrote down a set of equations which unified these two forces into a single theory. This led him to understand light waves (and radio waves) as electromagnetic oscillations propagating through a vacuum.
Light as electromagnetic waves
Waves on the surface of a pond are a sequence of peaks and troughs that move along in the shape of a sine wave. Light waves are mathematically similar, except that they are electromagnetic: the sinusoidal oscillation is of the amplitude of the electromagnetic field.
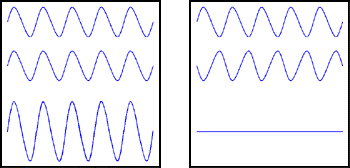
Figure 1: Light waves. In each box the sum of the first and second waves is the third wave.
When two waves of the same wavelength meet, their combined electromagnetic field depends on their relative phase. If the peaks of the two waves coincide, we say that the waves are in phase, and then the two waves reinforce each other, as in the left-hand box in the figure. But if the peaks of one wave coincide with the troughs of the other the waves are said to be out of phase, and they cancel each other, as in the right-hand box.
Try it : with a graphing calculator compare the graphs of sin(x) and sin(x)+sin(x). Then compare the graphs of sin(x), sin(x+pi) and sin(x)+sin(x+pi). What do you see?

Figure 2: The grooves on a CD are only 0.5 micro-metres wide and make a good diffraction grating, resulting in coloured interference patterns.
Because of the wave-like character of light, it is diffracted when it is shone through a pair of closely separated slits: if a screen is placed some way behind the slits, a pattern of light and dark fringes appears on it. The spacing of these fringes is calculated from the wavelength lambda of the light. Dark fringes appear at points on the screen where the light received from the two slits is exactly out of phase. These points have distances from the two slits that differ by:
where n is an integer.
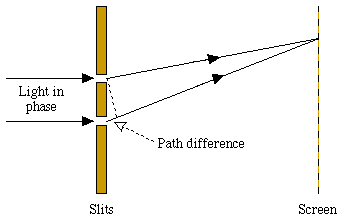
Figure 3: The double-slit experiment

Figure 4: Diffraction patterns are often used to analyse the structure of materials. Subtle differences in structure can change the properties of a material dramatically. Researchers at Heriot-Watt University are using the technique to help Cadbury make sure their chocolate always solidifies in the tastiest way.
Light as particles
So, by the beginning of the 19th century, it was a well-established notion that light is wave-like. But in the early years of the 20th century it became apparent that it is also particle-like. A key experiment was the photoelectric effect, in which electrons escape from the surface of a metal when it is bombarded with light.
A metal consists of a huge number of atoms effectively anchored to fixed sites by the electric forces caused by all the other atoms. The outermost orbital electrons of the atoms can easily be pulled off when an electric field is applied. They then move through the metal and form what we call an electric current.
When light is shone on the metal, some of the electrons can actually escape from the surface. The number that escape rises with the intensity of the light, but their energy of escape does not. Rather it depends on the colour of the light or, equivalently, its frequency nu (pronounced new).
The explanation of these properties by Albert Einstein in 1905 (the year in which he also produced the theory of relativity) was really the beginning of quantum theory. A beam of light can be thought of as a collection of particles, called photons. The number of photons is proportional to the intensity of the light, and the energy E of each photon is proportional to its frequency:
This formula had already been guessed in 1900 by the German physicist Max Planck, and the constant h is named after him. In ordinary units it is very small:
The electron is ejected from the metal when one of the photons hits it and gets absorbed by it, so that the photon's energy is transferred to the electron. The number of escaping electrons increases with the intensity of the light because when there are more photons there is a greater chance of one hitting an electron.
How heavy are photons?
Photons move with the speed of light, so when we think of them as particles we must use special relativity instead of Newton's mechanics. The energy of a particle whose speed is v (not to be confused with the greek letter nu) and whose rest mass is m is, according to Einstein:
In this equation m is the particle's mass, v is its speed and c is the speed of light. For a particle at rest we can substitute 0 for v giving Einstein's famous formula:
For a particle moving with the speed of light, v = c, the denominator vanishes, so it can have finite energy only if the numerator vanishes too, that is m = 0. Experiments have tested that photons have zero mass to very high accuracy: we know that their mass is less than 10-18 times that of an electron.
Photons may not have mass but they do have momentum. In Newton's mechanics the momentum of a particle is simply its mass times its velocity; p = mv. However, in special relativity the momentum of a particle is:
Try it : the Earth's mass is approximately 6x1024 kg, and it moves around the Sun once per year at a distance of about 1.5x1011 metres. Use a calculator to compare Newton's classical value for the momentum of the Earth with Einstein's relativistic value. The speed of light is approximately 3x108 ms-1.
What do you notice about the two values?
Using the relativistic momentum equation we can express the energy of a particle in terms of its momentum as follows:
For a photon this is simply:
But as we have seen already the energy is also related to the frequency of the light by:
When we combine these two equations, we find that:
This tells us the momentum of a photon for light of frequency nu.
For waves whose speed is c, the wavelength is:
Putting these formulae together we find that:
This is one of the fundamental relations of quantum theory!
It turns that this equation is so fundamental that it applies to all particles, not just photons. (See "Quantum uncertainty" elsewhere in this issue.).
Try it : using an approximation for the momentum of the Earth in its orbit round the Sun, calculate its wavelengh, lambda. The the value of h, Planck's constant, is given above as approximately 6.626x10-34 Js.
What do you notice about the value?
Biographies of the mathematicians mentioned in the article are available from the "MacTutor history of mathematics archive":
The author
Professor Peter Landshoff is doing research on quarks (what we and everything in the world are made of) and is a lecturer in quantum mechanics at the University of Cambridge.
Comments
Anonymous
The functions mentioned above can be viewed with https://www.wolframalpha.com
Anonymous
Fascinating and understandable at the same time.