
Magnetic tangles

Figure 1: Magnetic fields, from a bar magnet to the Sun. The global solar corona on the right was seen from Earth during a 2008 total eclipse. (Image on the right by Miloslav Druckmüller.)
What happens when magnetic fields get tangled up in knots? This does happen in the Sun's atmosphere and mathematical models predict that once the magnetic field becomes tangled, it must retain some vestige of this complexity for a long time. This enables the storage of vast quantities of energy. In this article I will outline how the notion of magnetic topology helps us to understand the physical situation and draw such conclusions.
Magnetic field lines: are they not those orderly patterns mapped out by iron filings around bar magnet, revealing the direction of an invisible force field? On a much larger scale, the Sun's magnetic field is also revealed in beautiful images, such as those taken in visible light during total eclipses. Here, the iron filings are replaced by electrons which emit the light, but the effect is the same. At first glance, the Sun's magnetic field has north and south poles akin to an astrophysical bar magnet, but take a closer look and it is rather different. The Sun is not a solid but a churning ball of plasma — a gas so hot that its atoms have been stripped of their electrons which are then able to conduct electricity. But electric currents generate their own magnetic fields, so we might expect the solar magnetic field to be complex and ever-changing. It is.

Figure 2: Magnetic loops in the solar corona, taken by the TRACE satellite. The inset shows how the coronal field lines are braided by random motions on the solar surface. (See also the TRACE movie, looking down on the solar surface.)
The magnetic field lines in the Sun's corona (the atmosphere above its visible surface) are rooted inside the Sun. The footpoints of these field lines, where they penetrate the surface, are dragged around by the random, turbulent motions inside the Sun. As a result, the coronal magnetic field can become braided and tangled. This tangling has important consequences, as we shall see.
Tangling prevents relaxation
Suppose that our coronal magnetic field has been tangled by motions in the solar interior, in the manner described. What happens then? The plasma in the corona is free to move around, and the tangled magnetic field will cause electric currents and flows of plasma. These in turn will re-organise the magnetic field. However, these motions rapidly use up energy, and eventually a final "relaxed" state is reached where all forces are balanced and the magnetic field is stationary. The process is called magnetic relaxation. The relaxed state of minimum possible energy is one where not only is the plasma stationary (because moving takes kinetic energy), but also there are no electric currents (because these involve the movement of electrons).
If this were all there were to it, then the Sun's magnetic field would relax very rapidly to this minimum energy state, and its coronal field would lose its tangling at the same rate it were gained. But observations have demonstrated that the Sun's magnetic field is not in this minimum energy state. Chief among these is the unintuitive fact that the corona is much hotter than the solar surface beneath. The only way that this could be theoretically possible is if the coronal magnetic field contains free energy above that of the minimum energy state. Could the tangling by surface motions be somehow preventing the relaxation?
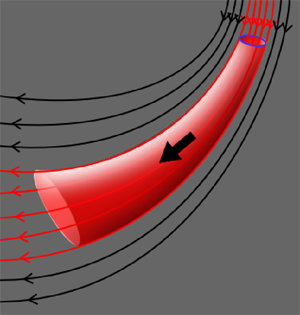
Figure 3: A bundle of magnetic field lines passing through a closed curve (in blue) is called a magnetic flux tube.
Mathematical modelling demonstrates that the tangling can indeed do this. The first indications came in the 1940s, when Swedish physicist Hannes Alfvén made the major advance of recognising that severe constraints arise from the very high electrical conductivity of the solar plasma. He was later awarded the 1970 Nobel Prize in Physics for his pioneering work on the dynamics of magnetic fields.
Alfvén's constraints are summed up in his frozen flux theorem. He proved that the mathematical equations of motion for a perfectly conducting fluid require that magnetic field lines move with the fluid. This means that if two blobs of plasma are connected by a magnetic field line at any time, they must be connected by a magnetic field line at all other times, past and future, even as the plasma moves around and the magnetic field is distorted. The consequences are far-reaching, implying that the precise manner of inter-linking, or tangling, of all of the field lines must also be preserved. In a perfectly conducting plasma, therefore, the magnetic relaxation can deform the magnetic field (by reshaping the plasma), but only so long as the links between different field lines, the magnetic topology, is preserved.
To give you an intuitive feeling for this topology preserving relaxation, I now introduce the notion of a magnetic flux tube. This is nothing more than a bundle of magnetic field lines passing through some closed curve (see illustration). Because the sides of the flux tube are formed of magnetic field lines, there can be no field lines entering the tube through the sides. So a cross section anywhere along the tube will always be cut by the same number of field lines, in the same direction. This is called the magnetic flux of the tube (because the magnetic field "flows" through the cross section in the direction of the arrows). Of course, the flux tube can get fatter or thinner as you move along its length. Where it is thinner, the magnetic field strength is higher, in the same way that for the bar magnet the magnetic force is stronger where the field lines converge near the poles of the magnet.
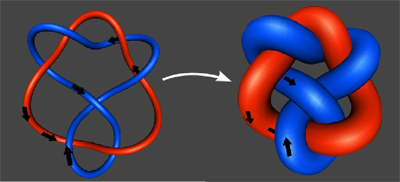
Figure 4: Linking limits the fattening of magnetic flux tubes as they relax.
So what happens to a flux tube during the relaxation? Well, the magnetic field will tend naturally to reduce its own energy during the relaxation, as well as the kinetic energy. Since the energy stored in a magnetic field is proportional to the strength of the field, flux tubes will try to evolve so as to get fatter. But, in general, a flux tube will be tangled around other flux tubes, or even knotted itself. It can fatten only until it comes into contact with itself or another tube. By Alfvén’s theorem, flux tubes can never pass through one another. So we see how the initial tangling affects the possible relaxation and will likely prevent it from reaching the minimum energy state.
A family of constraints
There is a simple way to quantify the linkage of a pair of closed flux tubes in the magnetic field. The flux tubes exist in three-dimensional space and do not intersect one another, but when we look at them from some direction we see a two-dimensional projection, with a number of crossings. The number of crossings we see depends on our viewpoint. Now, at each crossing, one tube is in front of the other, and each tube has a direction (that of its magnetic field lines). Suppose we call a crossing positive if the top strand must be rotated in the anti-clockwise direction to align it with the bottom strand. Conversely, call a crossing negative if the top strand must be rotated clockwise. If we do this for all possible crossings, we can count the total number of positive and negative crossings as seen from our viewpoint, which we label $N_+$ and $N_-$ respectively. These numbers can change if we move to a different viewpoint. But a remarkable fact is that the sum $$L = (N_+ - N_-)/2$$ is always the same, no matter which viewpoint we choose. This is called the linking number of the two tubes. Moreover, even if we stretch and deform the two tubes (without breaking them), $L$ will remain the same: it is a topological invariant. The only way to change it is for one tube to pass through the other. For a magnetic field, Alfvén's Theorem in a perfectly conducting plasma says that this cannot happen.
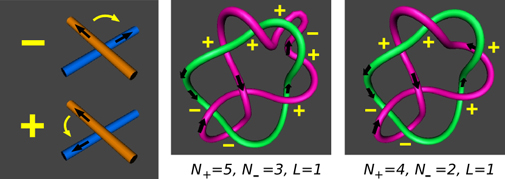
Figure 5: Definition of positive and negative crossings (left). On the right are two pairs of linked tubes, illustrating how deforming them can change N+ and N-, but not L.
In fact, the linking number has to remain the same for every possible pair of flux tubes that make up the magnetic field. So if we assume the coronal plasma to be perfectly conducting, then there are a whole family of constraints preventing the relaxation.
In reality the situation is not quite so simple. Alfvén's frozen-flux theorem relies on the assumption of perfect, that means infinite, conductivity. But of course the conductivity is not really infinite, just very (very) high. Unfortunately, the behaviour of a magnetic field in this case is fundamentally different from the (ostensibly very similar) case with truly infinite conductivity.
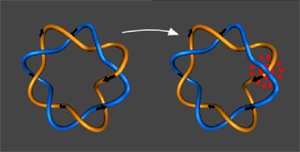
Figure 6: A localised "reconnection" can change the global linking number of two flux tubes.
A very small but finite resistivity leads to the dissipation of a little energy from the electrical currents as heat. In practice, this dissipation occurs only in localised pockets where there happen to be very high concentrations of current. Because Alfvén's theorem does not hold in these pockets, the magnetic field lines and flux tubes passing through those locations can change their connection. This is known as magnetic reconnection. But remember that the linking number is invariant only so long as the two tubes do not pass through one another. So two flux tubes that happen to cross in such a non-ideal pocket can change their linking number. In other words, even if Alfvén's theorem breaks down only in very localised regions, this can still change the global linkage of flux tubes.
What, then, prevents the relaxation from removing all tangling and reaching the minimum energy state? Physicists have realised that, although the family of linking constraints is destroyed by the presence of non-zero resistivity, a certain quantity representing the average linking number is not. This single number for the overall magnetic field is called the magnetic helicity H (see here for more detail on the magnetic helicity). You can see that H doesn't change in the perfectly-conducting case because each of the individual linking numbers are unchanged. What is less obvious is that H is almost conserved in the more realistic case of finite resistivity. Nevertheless, this has been shown mathematically from the dynamical equations, provided that the pockets of reconnection are small. The conservation is not perfect, so H would eventually decay away. But the decay is so slow that before it can change appreciably the coronal magnetic field will have been re-tangled by new surface motions anyway. So in an overall sense, tangling must persist for long times. The fact that the magnetic field must retain its magnetic helicity then means that it is prevented from relaxing to the minimum energy state.
Down to Earth with a bang

Figure 7: The Aurora Australis (southern lights) on 24 May 2010, seen unusually from above by the International Space Station. (Image courtesy NASA)
The notion of magnetic helicity conservation is not purely mathematical. Not only do we infer its presence by the hot corona, but we can measure it directly in so-called interplanetary coronal mass ejections. The Sun's magnetic field is not confined to its lower atmosphere but extends out into the solar system. If the magnetic field in the lower corona becomes too tangled (or perhaps tangled in a certain way), then it can become unstable and explode outward. Modern satellites allow us to track these ejections as they travel out toward Earth. Onboard instruments measure the magnetic field of the ejections, and have shown them to be tangled. When they arrive here and crash into our magnetosphere, they often send streams of high-energy particles down into the atmosphere. These are responsible for the aurora (Northern lights), and can even damage power and communication infrastructure on the ground. If the coronal magnetic field were in a simple, untangled, minimum-energy state, none of this would happen.
About the author

Anthony Yeates is a postdoctoral researcher in mathematics at the University of Dundee, where he is a member of the MHD (MagnetoHydroDynamics) research group. He tries to understand the workings of magnetic fields such as the Sun's by combining computer simulations and mathematical approaches like those in this article.
Figures 4 to 6 in this article were produced using a programme called KnotPlot.
The image of the Sun at the top left of this article is courtesy NASA.