Strategic dating: The 37% rule

Are you stumped by the dating game? Never fear — Plus is here! In this article we'll look at one of the central questions of dating: how many people should you date before settling for something a little more serious?

It's a tricky question, and as with many tricky questions, mathematics has an answer of sorts: it's 37%. Out of all the people you could possibly date, see about the first 37%, and then settle for the first person after that who's better than the ones you saw before (or wait for the very last one if such a person doesn't turn up).

Is this the one?

Why is that a good strategy? You don't want to go for the very first person who comes along, even if they are great, because someone better might turn up later. On the other hand, you don't want to be too choosy: once you have rejected someone, you most likely won't get them back. But why 37%? It's a question of maximising probabilities.

The basics

Let's first lay down some ground rules. We'll assume that you have a rough estimate of how many people you could be dating in, say, the next couple of years. Let's call this number $N$. The value of $N$ depends on your habits — perhaps you meet lots of people through dating apps, or perhaps you only meet them through close friends and work. Either way, we assume there's a pool of $N$ people out there from which you are choosing. And since the order in which you date people might depend on a whole range of complicated factors we can't possibly figure out, we might as well assume that it's random. 

We'll also assume that you have a clear-cut way of rating people, for example on a scale from 1 to 10. That in itself is a tricky task, but perhaps you can come up with some system, or just use your gut feeling. Sadly, a person you have dated and then rejected isn't available to you any longer later on. Among your pool of $N$ people, there's at least one you'd rate highest. We will call that person X — it's who you'd ideally want to end up with. Your strategy is to date $M$ of the $N$ people and then settle with the next person who is better. Our task is to show that the best value of $M$ corresponds to 37% of $N$. We'll do that by calculating the probability of landing X with your strategy, and then finding the value of $M$ that maximises this probability. Before we start, here's a picture of the end result. It shows the values of $N$ on the horizontal axis and the best value of $M/N$, the one that maximises the probability of ending up with X, on the vertical axis. You can see that, as $N$ gets larger, the optimal value of $M/N$ settles down nicely to around $0.37$. Which means that the best value of $M$ is roughly 37% of $N$.

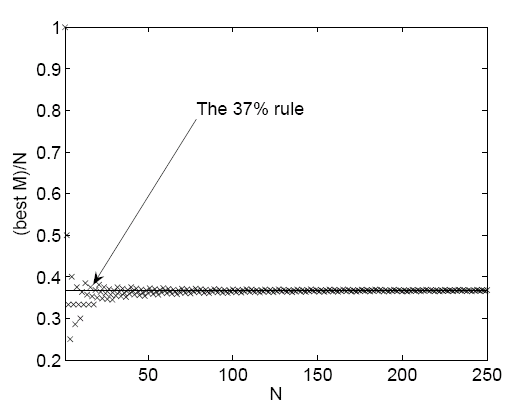
This figure was created by John Billingham for the article Kissing the frog: A mathematician's guide to mating, which looks at results and problems related to the 37% rule in more detail.

Getting in line

Let's calculate the probability $P(M,N)$ of picking X if you date $M$ people out of $N$ and then go for the next person who is better than the previous ones. Obviously it all depends on when you date X — right at the start, somewhere in the middle of your dating spree, or towards the end. The overall probability is therefore made up of several terms: \begin{eqnarray}P(M,N) &=& P(\mbox{X is your first date and you pick them})\\ & +& P(\mbox{X is your second date and you pick them}) \nonumber \\ &+& P(\mbox{X is your third date and you pick them}) \nonumber\\ & +& ... \nonumber \\ &+& P(\mbox{X is your $N$th date and you pick them}). \nonumber\end{eqnarray} Let's work out the terms one by one. If X is among the first $M$ people you date, then tough luck, you have missed your chance. The probability of settling with X is zero. Therefore, the first $M$ terms of equation 1 are all zero. If X is the $(M+1)st$ person you date, you're in luck: since X is better than all others so far, you will pick X for sure. Therefore, \begin{eqnarray*} & P(\mbox{X is the $(M+1)st$ person you date and you pick them}) \\ =& P(\mbox{X is the $(M+1)st$ person you date}).\end{eqnarray*} Now all things being equal (which we assume they are) the probability of X being the $(M+1)st$ out of $N$ people is $1/N$ (X is equally likely to be in any of the $N$ possible positions). Therefore, \begin{eqnarray*}& P(\mbox{X is the $(M+1)st$ person you date and you pick them}) \\=& P(\mbox{X is the $(M+1)st$ person you date}) \\ =& 1/N.\end{eqnarray*} If X is the $(M+2)nd$ person, you'll pick them to settle down with as long as the $(M+1)st$ person didn't have a higher rating than all the previous $M$ people. In other words, you pick X if the highest-ranked among the first $M+1$ people turned up within the first $M$ people. The probability of that is $M/M+1$. The chance of X coming $(M+2)nd$ is again $1/N$. Therefore \begin{eqnarray*} & P(\mbox{X is the $(M+2)nd$ person you date and you pick them}) \\ = &1/N \times M/(M+1) \\ = & M/(N(M+1)).\end{eqnarray*} Let's move on. If X is the $(M+3)rd$ person you date, you'll pick them to settle down with as long as the $(M+1)st$ person and the $(M+2)nd$ person both didn't have a higher rating than the ones you saw before them. In other words, you pick X if the highest-ranked among the first $M+2$ people turned up within the first $M$ people. The probability of that is $M/M+2$. The chance of X coming $(M+3)rd$ is again $1/N$. Therefore, \begin{eqnarray*} & P(\mbox{X is the $(M+3)rd$ person you date and you pick them}) \\ = & 1/N \times M/(M+2) \\ =& M/(N(M+2)).\end{eqnarray*} We can continue like this until we hit the case in which X is the last person you date. You will pick X as long as the $(M+1)st,$ $(M+2)nd$, $(M+3)rd$, etc, and $(N-1)st$ people all didn't have a higher rating than the ones you saw before them. In other words, you pick X if the highest-ranked among the first $N-1$ people turned up within the first $M$ people. The probability of that is $M/N-1$. The chance of X coming $Nth$ is again $1/N$. Therefore, \begin{eqnarray*} & P(\mbox{X is the $Nth$ person you date and you pick them}) \\ = & 1/N \times M/(N-1) \\ =& M/(N(N-1)).\end{eqnarray*} Putting all this together shows that \begin{eqnarray*}P(M,N) &=& \frac{1}{N}+\frac{M}{N(M+1)}+\frac{M}{N(M+2)} + ... +\frac{M}{N(N-1)}\\ &=&\frac{1}{N} \left(1 + \frac{M}{M+1} + \frac{M}{M+2} + \ldots + \frac{M}{N-1} \right) \\ &=&\frac{M}{N} \left(\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right).\end{eqnarray*}

Maximising your chance of success

For a given number of $N$ people you want to choose $M$ so that you maximise $P(M,N)$. This means that we want $$P(M-1,N) < P(M,N).$$ Substituting the expressions for $P(M-1,N)$ and $P(M,N)$ from the equation above and manipulating the inequality gives \begin{eqnarray*}1 < \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1}.\end{eqnarray*}

(See this article for the detailed calculation.)

We can go through the same calculation for $P(M+1,N) < P(M,N)$ and find that \begin{eqnarray*}1 > \frac{1}{M+1} + \frac{1}{M+2} + \frac{1}{M+3} + \ldots + \frac{1}{N-1}. \end{eqnarray*} Now let's play with some numbers. If $N=4$, so there are only four people, the only value of $M$ that satisfies the two inequalities is $M=1$, which is 25% of $N$: $$\frac{5}{6} = \frac{1}{2} + \frac{1}{3} < 1 < \frac{1}{1} + \frac{1}{2} + \frac{1}{3} =\frac{11}{6}.$$ This means you should discard the first person and then go for the next one that tops the previous ones. If $N=5$, so there are only five people, the only value of $M$ for which the two inequalities hold is $M=2$, which is 40% of $N$: $$\frac{7}{12}=\frac{1}{3} + \frac{1}{4} < 1 < \frac{1}{2} + \frac{1}{3} + \frac{1}{4} = \frac{13}{12}.$$ So you should discard the first two people and then go for the next one that tops the previous ones. These percentages are nowhere near 37, but as you crank up the value of $N$, they get closer to the magic number. For twenty potential partners ($N=20$) you should choose $M=7$, which is 35% of $N$. For fifty ($N=50$) you should choose $M=18$, which is 36% of $N$. For a hundred potential partners ($N=100$) you should choose $M = 37$ (that's obviously 37% of $N$) and for (an admittedly unrealistic) 1000 ($N=1000$) you should choose $M = 368$, which is 36.8% of $N$ .

Here's the plot of the best value of $M/N$ against $N$ again, confirming the 37% rule.

This figure was created by John Billingham for the article Kissing the frog: A mathematician's guide to mating, which looks at results and problems related to the 37% rule in more detail.

There's actually a more rigorous way of estimating the proportion, rather than just drawing a picture, but it involves calculus. If you follow that argument, you will see that the "about 37%" really mean a proportion of $1/e$ where $e$ is the base of the natural logarithm: $e \approx 2.718$ so $1/e \approx 0.368$. Those who are interested should read this article, which looks at the problem in terms of a princess kissing frogs and has the detailed calculations.

So what's your chance of ending up with X with the 37% strategy? It's roughly 37%! The magic number 37 turns up twice in this context, both as the probability and the optimal proportion. This comes out of the underlying mathematics, which you can see in the article just mentioned. Thus, using the 37% strategy your chance of ending up with X is just over a third. That's not great odds, but, as we have seen, it's the best you can expect with a strategy like this one.

Does it really make sense?

Happiness at last!

So should you use this strategy in your search for love? That's up to you. Real life is much more messy than we've assumed. Sadly, not everybody is there for you to accept or reject — X, when you meet them, might actually reject you! In real life people do sometimes go back to someone they have previously rejected, which our model doesn't allow. It's hard to compare people on the basis of a date, let alone estimate the total number $N$ of people available for you to date. And we haven't addressed the biggest problem of them all: that someone who appears great on a date doesn't necessarily make a good partner. Like all mathematical models our approach simplifies reality, but it does, perhaps, give you a general guideline — if you are mathematically inclined.

Our dating question belongs to the wider class of optimal stopping problems — loosely speaking, situations where you have to decide when is the right time to take a given action (go for a relationship) after having gathered some experience (dated some people) in order to maximise your pay-off (romantic happiness). Life abounds with these kind of problems, whether it's selling a house and having to decide which offer to take, or deciding after how many runs of proofreading to hand in your essay. So even if you prefer to keep your romantic life well clear of mathematics, strategies like the 37% rule might help you with other tricky problems life decides to through at you.

About the author

Marianne Freiberger is Editor of Plus.