
Kissing the frog: A mathematician's guide to mating
When you were small, you probably heard the fairytale The Frog Prince. The original version of the story is rather more complicated.
The Frog Prince: original version
Once upon a time, a princess was walking through a forest and stumbled across a pond. Out of the pond rose a witch, who cackled, "Stop! I have turned a handsome prince into a frog and cast him into my pond to live with 99 other frogs. Each frog has a different number on his back. The prince has the largest number on his back, and this is your only way of spotting him. You must find him and kiss him if you want to leave my enchanted forest. The frogs will jump from the pond one by one. When each frog appears, you must decide whether to kiss him or throw him back in, never to be seen again. If you kiss a real frog, or don't kiss any of the 100 frogs, you will never leave the forest, and the prince will remain in the pond." And with a suitably evil laugh, the witch sank back into her murky pond. Fortunately, the princess was very good at maths, and knew the best strategy for deciding which frog to kiss.

A prince?
Frog 1 hopped out of the pond with the number 2 on its back. The princess kicked it back into the pond. Frog 2 had the number 12 on its back. Better, but it received the same treatment from the princess. Frog 3 was number −6 (Did I say the numbers had to be positive?) and was duly dispatched by the princess. She repeated this for the first 37 frogs, and noted that the highest number she had seen so far was 23.2 (Did I say they had to be whole numbers?). She then waited until she saw a frog numbered higher than 23.2 and kissed it. (Of course the frog numbered 23.2 might have been the prince, and she'd then have missed him.) The frog disappeared in a puff of smoke to be replaced by a handsome prince, and they lived happily ever after (or, if you prefer unhappy endings: the witch rose from the pond laughing as the frog remained unmoved by the princess's attentions. Oh dear! There was a higher numbered frog still to come).
The 37% rule
The princess's strategy was first to gather some information about the frogs (she remembered the highest number out of the first 37), and then choose based on this information (she kissed the frog with the next highest number). If there were a different number of frogs, how many should she kick into the pond before looking for one worth kissing? The answer is that she should kick about 37% of the frogs into the pond. Why 37%? If you can count and you know that the integral of 1/x is ln x (now you know), then you should be able to follow the logical argument that leads to this conclusion.
Don't marry a frog!
If you haven't worked it out by now, I've been talking about partner choice. How many people should you date (and kick back into the pond) before you decide to settle down, live together and have babies (kiss the frog) based on how good a partner you think they'll make (the number on their back)? I've been describing a simple mathematical model for this important, life-changing decision. If you've never done any mathematical modelling, here's how it works:
- Find a real world problem.
- Try to decide what the important bits of it are.
- Translate these into maths.
- Forget the real world, and try to understand what the maths tells you.
- Compare with the real world.Choose between:
-
- Sitting back and gloating over your new-found insight before telling everyone how clever you are and what interesting new things you've discovered.
- Deciding that your model doesn't make sense, or doesn't agree well with the real world, then trying to figure out what features of the real world you left out. Go back to step 3.
Here's our example:
- Out of a limited choice of people, who should I choose to be my partner?
- Possible partners appear one after the other, I have no idea when or whether someone better will come along, and I want to choose the best possible partner.
- The fairy tale is the maths (honestly!).
- The best strategy is to date 37% of them, and then settle down with the next best one that comes along. This strategy pairs you up with the best partner 37% of the time.
- This is where it gets interesting. Does this strategy seem reasonable? Is there anything about the real process of partner choice that we have left out?
We can pass over 6a quickly, as there are so many things missing from our mathematical model that it's hard to know where to begin patching it up! However, we should briefly pat ourselves on the back, because the idea of dating a few people before settling down seems sensible, even though we might not be entirely convinced that the 37% rule is what real people either use or should use (37% of how many? Good question!). Now for step 6b.
How attractive is my frog?

Kissed too soon?
I'm told that when men meet women, they sometimes rate each other on a scale of 1 to 10. Of course, mathematicians are far too intelligent and sophisticated do this. We rate people on a scale of 0 to 1. In our original mathematical model, all we could do was compare one possible frog with another. The numbers didn't mean anything in themselves; they just told the princess whether one frog was "better" than another. Let's change the fairytale slightly so that the 100 frogs are now labelled with numbers drawn randomly from those that lie between 0 and 1, with the handsome prince having the highest number. What's the princess's best strategy now?
Well, the princess now has much more information to use. There is a highest and a lowest number (0 and 1), and the frogs' numbers are uniformly, but randomly, distributed between the two. If the first frog to hop out is numbered, for example, 0.99, then she knows it's a top quality frog, and could well be worth a peck on the cheek. What if the first frog is numbered 0.8? Is that good enough to kiss? It turns out that the best strategy is, as anyone aged over 25 knows, to start with high standards, and then lower them as the frogs keep on coming. We're meant to be doing some maths here, so by "standards" I mean that for each frog there is a number, called a decision number, below which the princess shouldn't kiss it (here's how to calculate the decision number). If the frog is numbered above the appropriate decision number, and is the best frog so far, she should kiss it. This strategy nets her the handsome prince a whopping 58% of the time. In fact, if the first frog is numbered 0.99, she shouldn't kiss it, because the first decision number for 100 frogs is about 0.992. She's more likely to find Mr. Right by holding out for a more attractive frog. Examples of the three things that can happen are shown below.
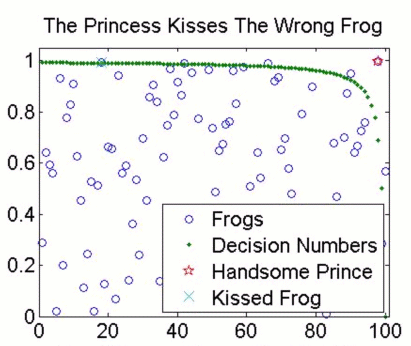
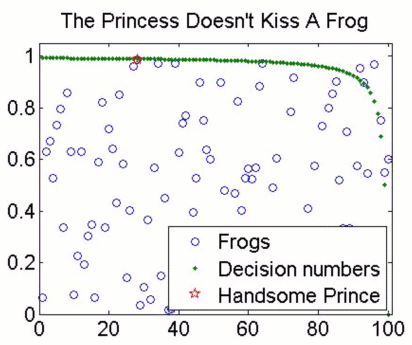
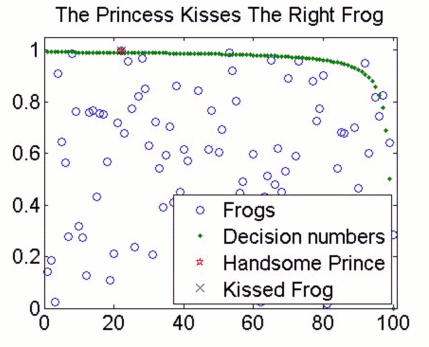
The best-looking frog ... but he doesn't fancy me .. and I don't know why not!

A frog's perspective.
There are lots of other things that we could add to our mathematical model to make it more realistic. For example, in real life, if you kiss the second best frog, you don't have to stay in the enchanted forest. Unless you're an incurable romantic who thinks that there's just one perfect person out there for you, you can be very happy with frog number 2. Maybe you're more interested in avoiding a very bad frog. What's more important, making sure you bag frog number 1 or avoiding frogs 51 to 100? The strategy you should choose depends upon what you're trying to achieve.
Now let's imagine that the princess, who I have so far avoided describing, has a face like a bag of spanners. When the handsome prince appears, he may take one look at her and run for his life. Partner choice is a two-way business. You must choose and be chosen. If you kiss a frog whose number is too far from yours, disaster is probably just around the corner. And how do you know what your number is anyway? You may think you know, but it's not what you think that matters. It's only by finding out who will agree to date you that you start to get some idea of what your number is. All of these features can be, and have been, added to mathematical models.
There's more to life than snogging
One of the great things about maths is that it has so many different uses. In fact, the same bit of maths can have lots of different applications, and the fairytale of the frog prince is an example of this. Let me retell the fairytale one last time. In this version, the princess's three brothers have been turned into frogs and thrown into the pond. She still has to find them by kissing them, the frogs are still numbered between 0 and 1 and her brothers have the three largest numbers. The witch is very generous and allows her to kiss 20 of the frogs. As long as her brothers get a kiss, all four of them can go home. If you think this sounds easy, you'd be right. In fact, with the right strategy, the chances of a brother missing out on his kiss are tiny. Again, there are decision numbers, but these are very low to start with, so that the princess's lips will be kept busy at the start of the parade of frogs. However, after each of the first two kisses, the decision numbers increase and, after she has kissed three frogs, she kisses any frog numbered in the top three so far.

Don't marry this.
So what's that got to do with partner choice? I don't know of anyone who arranges their love life in such a bizarre way. In fact, this is a mathematical model for a game played between the regulators and the suppliers of electricity in the UK. Part of the money paid by industrial customers to their electricity supplier is based on their consumption of electricity during the three half hour periods during each year when the total consumption of energy across the whole country is highest. From the regulator's point of view, this is meant to encourage industry to cut back its consumption during times when the national grid gets close to its operating capacity. From the point of view of a large industrial consumer of electricity, they want to know when these half hour periods are, so that they can shut down their factories and save themselves lots of money. The problem is that nobody knows when these three periods (called the triads) are until the year ends and the electricity consumption figures are added up. Industry is therefore prepared to pay a lot of money to anyone who can accurately predict these triad periods for them (call the triads). They know that they'll have to turn off their factories more than just three times to hit the triads reliably, but aren't prepared to do this more than about 20 times per year.
So, here's the fairytale again. Predictions of energy consumption appear in sequence (frogs jump out of the pond), we want to make sure we advise our customers to turn off their factories when we think this will be a triad (the princess must kiss her three brothers), but we mustn't do this more than 20 times (the princess can kiss no more than 20 frogs). If energy consumption figures were just random numbers between 0 and 1, this would be pretty easy, and no one would make any money from predicting triads.

'Kiss me!'
However, and here we're back at step 6b of my description of mathematical modelling, there are lots of complications. I'll tell you about just two of them. Firstly, energy consumption figures are basically random numbers, but each number depends to some extent on the number before, in the same way that the weather today is a reasonable predictor of the weather tomorrow. This means that we need another mathematical model for how these numbers behave, and, back in the real world, we have to predict them. Secondly, calling a triad affects the numbers that we're trying to predict. Say we predict that electricity consumption will be high enough to be a triad period, we call it, and our customers close down their factories. Electricity consumption is then lower than it would have been (which is, of course, why the regulators set up the game in this way). There is negative feedback built into the system. But we may still need to call the triad, because otherwise the factories stay on, electricity consumption is higher, and the princess's brother stays in the pond forever!
Further reading
The first fairytale is usually known as the secretary problem, and has spawned a vast amount of new mathematics over the last forty years. Although the solution appeared in a scientific paper in [1], there is some controversy over who was actually the first to solve it, [2].
The literature on partner selection is very large, and I'm no expert, but the most entertaining introduction I've read is given by Todd and Miller in [3].
Finally, if you want to learn more about calling triads, you'll have to read [4].
[1] J.P. Gilbert and F. Mosteller, 1966, Recognizing the maximum of a sequence, J. Am. Stat. Ass., 61, 35-73
[2] T. S. Ferguson, 1989, Who solved the secretary problem? Statist. Sci. 4, 282-289
[3] P.M. Todd and G.F. Miller, 1999, From Pride and Prejudice to Persuasion: Satisficing in mate search, in Simple heuristics that make us smart, eds. G. Gigerenzer, P.M. Todd and the ABC Group, Oxford University Press
[4] Robert Hunt, Liam Clarke, John Byatt-Smith and John Billingham, 2006, [ https://www.smithinst.ac.uk/Projects/ESGI56/ESGI56-BritishEnergy/Report] Forecasting triads: The negative feedback problem, Study Group Report
About the author

John Billingham is a Professor of Theoretical Mechanics in the School of Mathematical Sciences at the University of Nottingham. He is married to a beautiful princess who clearly knows nothing about the 37% rule.
Comments
Anonymous
Dear Dr. Billingham
Thanks for the wonderful lesson and story. I am a 30 year old adult and have always been a bit short on Mathematics knowledge. Lectures/lessons like yours help me to stay motivated to learn mathematics even at this point of age.
In the first part of the story, you said the number of the frogs have to a whole number, and the number that the Princess saw was 23.2, do you think 23.2 is a whole number?
Thanks.
Anonymous
actually, the evil witch just said that each frog would have a number. Therefore, they don't have to be integers.
Mayank Mukund Bhandare
Thank you so much for the wonderful analysis, Dr. John!
I happened to read this yesterday, on the eve of the Valentine's, and I didn't really regret not having a human Valentine (I have my two dogs who do make up for the same by the way!).
The credit goes to this mesmerizing article that I stumbled upon.
Wow! I mean, loved it.
Hats off to the beautiful soul (who probably believes in true love, now, whatever that may be!) who was indeed brilliant in coming up with the analysis (and somehow, stretching the probability of the method's viability to an appreciable 58%, finally!)
I would love to go through the Todd-Miller book as well. Thanks!
P.S. Well, in the 'Finding The Decision Numbers' section, I guess you seemed to have made a petty typo, is it? Third para. Last sentence. It must be {y^(k - j)}{(1 - y)^j}, right?
Not petty enough though! I wasted almost half an hour in figuring it out until something in me prompted me to scroll down, only to discover that it was nothing but a silly typo. Man!!
Please do consider editing the same, if possible.
Thank you!