Kissing the frog: A mathematician's guide to mating
The 37% rule
The first question we need to answer is, why is the best strategy to throw back some number of frogs, and then kiss the next one that is better than all those you've seen so far? Well, what else could you do? All you know about the frogs that you've seen is how good they are relative to each other, which you can see from the numbers on their backs. When the first frog hops out, you have absolutely no information (the number on its back tells you nothing). You could kiss it, but there's only a 1 in 100 chance that it's really the handsome prince. So you'd be better off waiting until you've seen a few more frogs ... and that's the strategy!
Let's make things a little more general. If there are $N$ frogs in the pond, you will kick back the first $M$ frogs, and then kiss the next frog that has a higher number than all those you have seen so far. We have to work out what the best choice of $M$ is. To do that, we have to work out what your chances are of kissing the right frog, depending on where he appears in the sequence:
If the handsome prince is one of the first $M$ frogs, disaster, you'll kick him back in the pond.
If he is the $(M+1)$th frog, success, you'll kiss him.
If he is the $(M+2)$th frog, you'll kiss him, {\em unless the $(M+1)$th frog had the largest number of all the previous $M+1$ frogs}. This unfortunate arrangement of frogs, which means that you'll kiss the $(M+1)$th frog, not the handsome prince, only occurs in $1/(M+1)$ of the possible ways of arranging the first $M+1$ frogs. (There are just as many arrangements that have the largest numbered frog in the last position, as there are arrangements that have the largest numbered frog in any other position.) You'll kiss the right frog in $1-1/(M+1) = M/(M+1)$ of the possible cases.
If he is the $(M+3)$th frog, you'll kiss him, {\em unless the $(M+1)$th or $(M+2)$th frog had the largest number of the previous $M+2$ frogs}. This only occurs in $2/(M+2)$ of the possible ways of arranging the first $M+2$ frogs. You'll kiss the right frog in $M/(M+2)$ of the possible cases.
...
And so on, until
...
If he is the $N$th frog, you'll kiss him, {\em unless the $(M+1)$th, $(M+2)$th, $(M+3)$th,\ldots or $(N-1)$th frog had the largest number of the previous $N-1$ frogs}. This only occurs in $(N-1-M)/(N-1)$ of the possible ways of arranging the first $N-1$ frogs. You'll kiss the right frog in $M/(N-1)$ of the possible cases.
Now, each of these possible positions of the handsome prince occurs in $1/N$ of the possible arrangements of the frogs, so your probability of winning is \begin{eqnarray*} P(M,N) & = & \frac{1}{N} \left(1 + \frac{M}{M+1} + \frac{M}{M+2} + \ldots + \frac{M}{N-1} \right) \\ & = & \frac{M}{N} \left(\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right).\end{eqnarray*} For a given total number of frogs $N$, we want to maximise your probability of kissing the handsome prince, $P(M,N)$, so we want $$P(M-1,N)< P(M,N) ~~\mbox{and}~~P(M+1,N) P(M,N)$$ starting with the first inequality means that \begin{eqnarray*} & \frac{M-1}{N} \left(\frac{1}{M-1} + \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right) \\ < & \frac{M}{N} \left(\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right).\end{eqnarray*} Cancelling the factor of $N$ gives \begin{eqnarray*} &(M-1) \left(\frac{1}{M-1} + \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right) \\ < & M \left(\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right).\end{eqnarray*} Now multiply out the first term of the top line to give \begin{eqnarray*} & 1 + (M-1) \left(\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right) \\ < & M \left(\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right).\end{eqnarray*} Take the right hand side over to the left to give \begin{eqnarray*}1 -\left(\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right) <0,\end{eqnarray*} and therefore \begin{eqnarray*}1<\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1}.\end{eqnarray*} We can go through the same calculation for $P(M+1,N) < P(M,N)$ (try it!), and find that \[1>\frac{1}{M+1} + \frac{1}{M+2} + \frac{1}{M+3} + \ldots + \frac{1}{N-1},\] so that, finally, we need \[ \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} < 1 < \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1}. \]
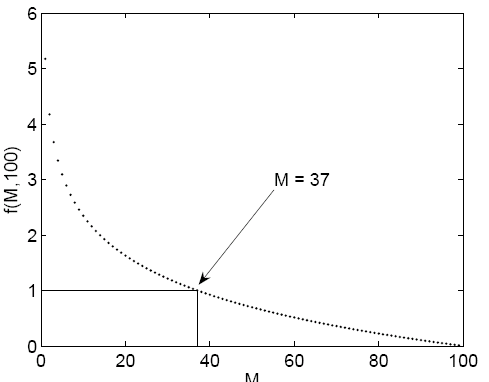
We can now work out what $M$ you should use for various numbers of frogs in the pond (values of $N$). If there are only four frogs, we can see that \[\frac{1}{2} + \frac{1}{3} < 1 < \frac{1}{1} + \frac{1}{2} + \frac{1}{3},\] so $M = 1$, and you should kick back the first frog, and kiss the next one that is better. If there are only five frogs, we can see that \[\frac{1}{3} + \frac{1}{4} < 1 < \frac{1}{2} + \frac{1}{3} + \frac{1}{4},\] so $M = 2$, and you should kick back the first two frogs, and kiss the next one that is better. We could continue doing this by hand, but it gets very tedious. Instead, let's define \[f(M,N) = \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1},\] and ask a computer to plot this function for us. For 100 frogs ($N=100$), we can see below that you should choose $M = 37$.
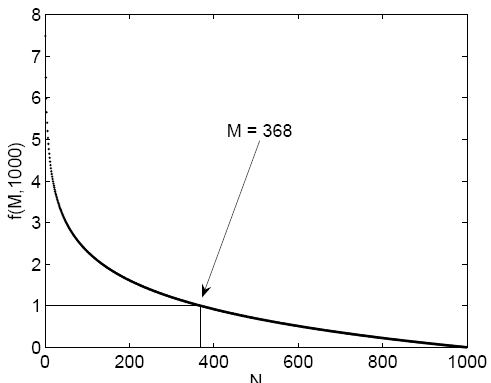
For 1000 frogs ($N=1000$), you should choose $M = 368$.
Let's plot the value of $M/N$ that you should choose as a function of $N$.
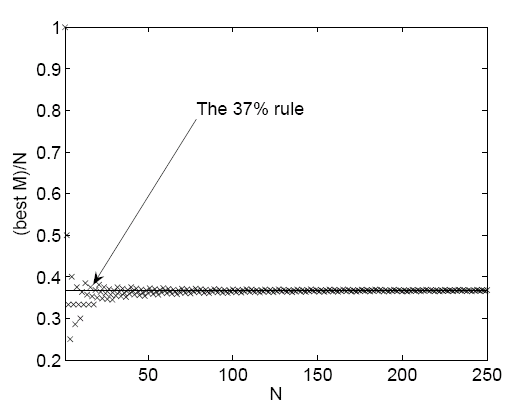
As $N$ gets bigger, we can see that the proportion of frogs that you should kick back before thinking about kissing asymptotes to about $37\%$. But why? Can we be more precise? Can we estimate the size of the function $f(M,N)$ when $N$ is large?
Have a look at the graph drawn below.
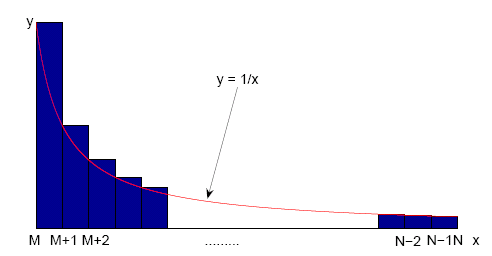
The area of the shaded blocks is $\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1}$. The curve drawn through the top left hand corners of the blocks is $y = 1/x$. We can see that the area under the curve is less than the area of the blocks, so \[\int_M^{N} \frac{1}{x} dx < \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \cdots + \frac{1}{N-1}.\] But \[\int_M^{N} \frac{1}{x} dx = \left[ \ln x\right]_M^N = \ln N - \ln M = \ln\left(\frac{N}{M}\right),\] so \[\ln\left(\frac{N}{M}\right) < \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \cdots + \frac{1}{N-1}.\]
Now look at the next graph.
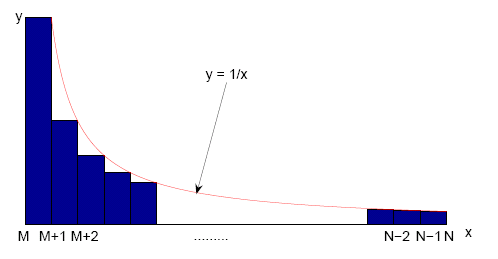
In this case, we can see that the area under the blocks (excluding the first block) is less than that under the curve, so \[\frac{1}{M+1} + \frac{1}{M+2} + \cdots + \frac{1}{N-1}< \int_M^{N-1} \frac{1}{x} dx= \ln\left(\frac{N-1}{M}\right).\] Putting this together, we can see that \begin{eqnarray*} & \frac{1}{M+1} + \frac{1}{M+2} + \frac{1}{M+3} + \cdots + \frac{1}{N-1} \\ < & \ln\left(\frac{N-1}{M}\right) < \ln\left(\frac{N}{M}\right) \\ < & \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \cdots + \frac{1}{N-1}.\end{eqnarray*} However, we are trying to find $M$ so that \[\frac{1}{M+1} + \frac{1}{M+2} + \frac{1}{M+3} + \cdots + \frac{1}{N-1} < 1 < \frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \cdots + \frac{1}{N-1}.\] When $N$ and $M$ are large, $N/M \approx (N-1)/M$, so we need to choose $M$ with \[\ln\left(\frac{N}{M}\right) \approx 1,~~~\frac{N}{M} \approx e,~~~M \approx \frac{N}{e} \approx 0.3679 N.\]
But how often does this net you the handsome prince? We found a while ago that the probability of kissing the right frog is \[P(M,N) = \frac{M}{N} \left(\frac{1}{M} + \frac{1}{M+1} + \frac{1}{M+2} + \ldots + \frac{1}{N-1} \right) \approx \frac{1}{e} \ln\left(\frac{N}{M}\right) \approx \frac{1}{e} \approx 0.3679.\] So the 37\% rule wins the prince 37\% of the time, whether there are a hundred, a thousand or a million frogs in the pond. Mind you, it might take a while to kiss 37\% of a million frogs. There's another thing to think about in our model!