Mathematical mysteries: The Solitaire Advance
Solitaire is a game played with pegs in a rectangular grid. A peg may jump horizontally or vertically, but not diagonally, over a peg in an adjacent square into a vacant square immediately beyond. The peg which was jumped over is then removed.

Starting with some arrangement of pegs, the pegs are jumped over each other until just one peg remains in a prescribed position.
There are many versions of the game. In the best-known version the board is cross-shaped, with pegs in every position except the centre. The object is to find a jumping procedure which will leave just one peg in the centre.
In "The Solitaire Advance" the problem is to arrange an "army" of pegs behind a line across the board, and then to jump them in such a way as to advance one of the pegs as far across the line as possible.
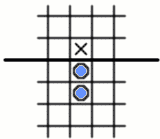
Just two pegs are needed to get one of them into the first row across the line,
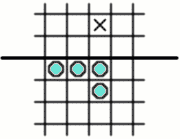
while four pegs can be arranged and jumped so as to advance a peg into the second row,
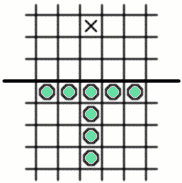
and an army of eight pegs can be arranged and jumped so as to advance a peg into the third row.
Setting out an army of pegs which can advance a peg into the fourth row is rather more challenging. One solution is shown. There are several others.
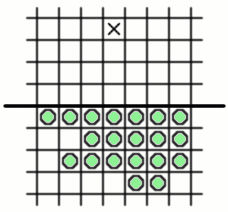
Can an arrangement be found to advance a peg into the fifth row beyond the barrier? This turns out to be rather difficult, and after some unsuccessful attempts the suspicion takes hold that the task may be impossible. But even the strongest suspicion is not enough. A convincing argument is needed, proving beyond doubt that it is not possible to find any arrangement of pegs behind the barrier that can be used to jump a peg into the fifth row.
Such an argument was devised by the mathematician John Horton Conway. It relies on an ingenious way of assigning values to the squares of the grid.
The value 1 is assigned to the target position in the fifth row, and the positions below that are assigned the values $x^r$, where $r$ is the smallest number of steps (horizontally or vertically) from that position to the target position.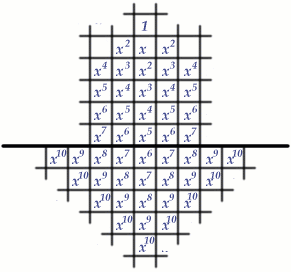
The value of $x$ is chosen to be the positive root of $x^2 + x = 1$ i.e. $x = {1\over 2}(\sqrt{5}-1)$ (the Golden Ratio). The reason for this choice is that it follows that $x^{r+2} + x^{r+1} = x^{r}$, for $r=0,1,2,\dots $.
Let us examine what happens when a jump is made. \par If three squares are in a row, there are two possibilities. The first is that they are labelled $x^{r+2}, x^{r+1} ,x^r$, for some $r=0,1,2, \dots $. The second possibility is that they are labelled $x^{r+1}, x^r ,x^{r+1}$, for some $r=0,1,2, \dots $. \par Considering the first possibility, suppose three squares in a row or column are labelled $x^{r+2}, x^{r+1} ,x^r$, for $r=0,1,2, \dots $, with the first two squares occupied and the third vacant. When the peg in the first position jumps over the peg in the second position into the vacant third position

the total value of the occupied squares stays the same, since $x^{r+2} + x^{r+1} = x^r.$ If a jump is made in the opposite direction

the total value decreases, since $ x^{r+2} < x^{r+1} + x^{r} \hbox{and} 0 < x < 1. $ \par Considering the second possibility, if three squares in a row or column are labelled $x^{r+1}, x^r ,x^{r+1}$, for $r=0,1,2, \dots $, with the first two squares occupied and the third vacant, then when the peg in the first position jumps over the peg in the second position into the vacant third position

the total value of the occuped squares also decreases. In summary: as the pegs are jumped, the total value of the squares occupied by the solitaire army stays the same, $vr$ decreases. We now calculate the total value $V_n$ of all squares below the barrier of value $x^n$ or more.
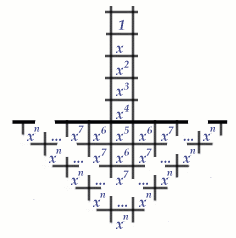
$$ V_n = x^5 + 3x^6 + 5x^7 +\dots \quad + (2n-1)x^n $$ This is a hybrid of an arithmetic and a geometric series, which may be summed by the same technique used in summing a geometric series\dots \par Multiply throughout the expression for $V_n$ by $x$ and subtract the result from the original expression. This gives $$ (1-x) V_n &= x^5 + 2x^6 + 2x^7 + \dots + 2x^r - (2n-1) x^{n+1}\cr$$ $$ = x^5 + 2x^6 \left(1+x+ \dots + x^{n-6})\right - (2n-1)x^{n+1}\cr &= x^5 + {2x^6(1-x^{n-5})\over 1-x} - (2n-1) x^{n+1} \cr } $$ summing the geometric series. \par So $$ \eqalign{ V_n &= {x^5(1-x) + 2x^b \over (1-x)^2} - {2x^{n-1}\over(1-x)^2} - {(2n - 1)X^{n+1}\over 1-x} \cr &< {x^5 + x^6 \over (1-x)^2} \qquad \hbox{(since} 0 < x < 1). } $$ Since $x^5 + x^6 = x^4$, and $1-x = x^2$, it follows that $V_n < 1$ for all $n$. Therefore any arrangement of pegs below the barrier has total value less than $1$, and that proves that no arrangement can be found that will advance a peg into the fifth row.