Mathematical Mysteries: Trisecting the Angle
Bisecting a given angle using only a pair of compasses and a straight edge is easy. But trisecting it - dividing it into three equal angles - is in most cases impossible. Why?
Bisecting an angle
If we have a pair of lines meeting at a point O, and we want to bisect the angle between them, here's how we do it.
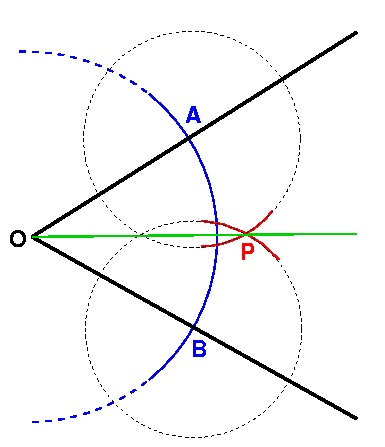
Bisecting angle AOB using straight edge and compasses.
Put the point of the compass at O and draw a circle (of any radius you like). This is the blue arc in the diagram. The circle will cross the two lines at two points: call these A and B.
Now put the point of the compass at A and draw an arc of a circle, as shown in the diagram. Without changing the radius at which the compass is set, move its point to B and draw another arc of a circle. These are the red arcs in the diagram. The point where the two arcs cross, P, can then be joined to O using the straight edge (the green line), and angle POB is half of angle AOB. If the arcs don't cross, then of course you need to use larger circles!
Trisecting an angle
What about trisecting an angle? Why is it so difficult? There are a few special cases of angles for which it can be done - for example, pi/2 radians (90 degrees). For the general case, however, the Greeks couldn't work out how to do it, despite expending vast amounts of energy on the problem.
Trisecting an arbitrary angle can be done if you cheat by using a measuring ruler instead of a plain straight edge (you can find out how in the sci.math FAQ file), or even if you simply draw two little marks on your straight edge. However, to "play by the rules" you aren't allowed any marks on the straight edge at all - it must be completely blank.
The problem of whether trisection could be done in the general case remained a mathematical mystery for millennia - it was only in 1837 that it was eventually proved to be impossible by Pierre Wantzel, a French mathematician and expert on arithmetic. This was a great achievement for a man of 23, who subsequently died at the tragically young age of 33.
So why is it impossible? Pierre showed that the two problems of trisecting an angle and of solving a cubic equation are equivalent. Moreover, he showed that only a very few cubic equations can be solved using the straight-edge-and-compass method - most cannot. He thus deduced that most angles cannot be trisected.
Footnote : The real mystery
Despite the fact that Wantzel's proof means that we now know that it's impossible to trisect a general angle, people keep trying. The mathematics department where PASS Maths is based receives quite serious letters every so often from individuals who think they've cracked the problem, offering famous people in the department the opportunity to "buy" the "proof" (sometimes for large amounts of money!). One such letter even missed out several pages of the "proof" on the grounds of security of the writer's copyright!
Needless to say, all these so-called proofs contain flaws and are worthless. If the writers really wanted to convince anyone that it is possible to trisect the angle, their time would be better spent trying to find an error in Wantzel's proof. The real mystery here is why people keep trying to solve the problem in the face of a proof of its impossibility. How would you reply to them?
Comments
Anonymous
Ha. Logically it is not possible to prove that something is impossible.
Anonymous
Prove it.
Anonymous
Dear anonymous
Mathematicians prove the impossible all the time. One such example is the proff that it is impossible to find the ratio of two integers that equal the square root of two.
touche!
Anonymous
No! That is NOT proving the impossible. Rather, its proving impossible something (huh?). As in, its "un"-proving something.
Anonymous
Actually the aphorism is that it's not possible to prove a negative (and even that is sometimes wrong). Proving that things are impossible is done all the time... it is the basis, for example, of reductio absurdum or proof by contradiction.
Marty
bisect line oa, join a to b bisect this line, take the centre of oa and project it through the centre of ab so that projected line is equal lenght inside and outside the triangle then take the point at the end of projected line run it back to o. looks like 1 third to me
Anonymous
An angle can be trisected by Euclidean methods in 3 dimensional space.
Anonymous
In regards to people tackling a proof trisecting an angle, a case can be made that it isn’t always a worthless endeavor. In my case I am looking at it as a way to keep my mind and thinking active.
The easiest thing to do is to prove that it is impossible to trisect any angle precisely. However there is still the question of is there any method to effectively trisect any angle to an acceptable accuracy in a limited number of steps using only a compass and unmarked straight edge. This is a different issue and is a valid question.
Anonymous
|I recomend to you my comment at the top ofthe column of comments: I claim that it works: Straightforward in angles between 0 and 180, higher angles need to be partitioned into a straight angle ( tri is 60 easy) and an acute or obtuse angle the smaller ( or residual) angle is then trisected using my described technique asnd then the trisect copied to augment the angle of 60 derived from the straight angle, the composite angle being one third of the original angle
Anonymous
1) Set up the angle in a circle centring its midpoint
2) Build a triangle using the chord as height
3) Find the Centroid on the chord
...draw your lines and see what may be the real thing
and something you can't prove
gkmk2030
1) Draw AB
2) Draw AC orbitrarily
3) With any radius with compass mark D along AC and E along AB
4) Join DE
Problem :
We have to divide DE to 3 equal parts
1) With D as center mark DF (any distance) arc and with same radius and compass mark FG with F as center and
GH with G as center along AC
2) Join HE
3) With GK as radius mark a circle with E as center . join GL (L is the outer most point in circle)
4) with the top most point L joint G & L with a line
5) Similarly with FN as radius draw a circle with center as I and join MF intersecting DE at J (J is the outer most point in circle)
6) Join AJ, AI
7) Hence angle BAC is divided into 3 parts
By H.S. TANDAVESHWARA dated 19/12/2014
Anonymous
WITHOUT GIVING ANY PREVIOUS HINTS, YOU HAVE USED POINTS LIKE 'K', 'N', 'I' AND 'M' WHILE SAYING GK, FN AND MF. SIMILARLY WHILE SAYING 'OUTER MOST POINT OF A CIRCLE' YOU SHOULD HAVE BEEN MORE PRECISE AS THERE ARE TWO SUCH POINTS FOR A POINT LYING OUTSIDE THE CIRCLE. I THINK THERE ARE EASIER WAYS OF DIVIDING A LINE INTO 3 EQUAL PARTS.
BUT MOST IMPORTANT: DID YOU MEASURE THE THREE ANGLES CREATED AT 'A'? CAN YOU PROVE THAT THE ANGLES ARE OF EQUAL MEASURE?
Prasenjit Wakode
We divide any angle by this method into the ratio of x:y:x but not x:x:x so the trisection method you proposed is actually a method for partitioning an angle into ratio x:y:x (where values of x and y can be calculated for general case. You can try it and show that x is not equal to y !!!). Talking generally, we can divide any arbitrary angle into a paliandromic ratio by this chord sectioned method.(i.e. for 5 parts, angle wil be divided into ratio a:b:c:b:a , etc). There are different auxilliary curves like hyperbola(for trisection only), spiral(for n section), sinusoidal wave(for n section), etc which can trisect or nsect any given angle. Sometimes only intuition can give wrong results bro so read more and derive more.
Anonymous
The section on bisecting an angle with Euclidean compass and straight edge contains errors.
First, you may not draw a circle with an arbitrary radius ("any radius you like"). The only thing you can do with a Euclidean compass is to draw a circle with the center at a known point, and the circumference containing a known point. You cannot just "pick a point," you must construct it. This problem can be avoided by instead drawing the circle with center at the vertex of the angle, and through one of the other two points that are given to define the angle. Restatement: given angle ABC (B the vertex), draw the circle with center B and radius the length of segment AB.
Second, when you lift a Euclidean compass off the paper, it collapses. You cannot just move the compass and keep it set at the same radius.
Mike Ochs
B.A. Mathematics, Univ of Colorado
Anonymous
The compass equivalency theorem basically states that you can construct with an unmarked straight edge and collapsing compass two circles of equal radii around 2 arbitrary points on a plane. By the application of this theorem, you can justify the use of a rusty compass in your constructions.
Anonymous
Given any angle ABC
Centre the vertex draw an arc to cut the two arms: AB in P BC in S
Join PS
Centre P and radius = PS draw a long seeking arc.
Centre S and radius PS, draw a defining arc to cut the arc centre P inD
Join DB
BD will cut PS at its mid point, E
Centre E and radius EP draw a semi circle to cut PS at P and S.
Centre P and radius EP draw an arc to cut the semi circle centre E at Q
Centre S draw an arc radius ES, to cut the semicircle centre E at R
Join BQ, BR these lines will trisect thew circle.
The development of this technique rests on the extension of the Basic circle equality: equal chords in the same circle subtend equal angles at the circumference.
Given three equal adjacnt angles from the centre of a circle, then the subtending arcs will subtend three equal adjacent angle at any point on any concentric circle.
My paper which is being stolidly ignored by academia, (is in fact copyright) and contains euclidean style proofs leading up to and including the new equal angles proposition. I am willing to share the entire paper with anyone hwo promises to honour the copyright.
Anonymous
Sir, try your construction in auotocad and then actually measure all the three angles that you feel are one third the original one. I have tried as per the steps you mentioned but it isn't trisecting at all. It in fact dividing the original angle in the ratio x:y:x . But a good try indeed.
Anonymous
I can do it if I invoke the Goldilocks theorem. It's that ok?
Paul506
I have done this using only 1 compass and 1 unmarked straight edge. I'd be happy to demonstrate and be proven wrong but I have no idea of the best place to go.
Dave_
I've found over the years that "impossible" has a certain feeling associated with it...so when I make these attempts I actually train my brain for other math related and conceptual work.
David Scott Stokes
Yes, I do believe it is possible. I am fine tuning my method which is quite simple to understand. stokes.scottd@gmail.com
Petrus3743
Yes, it is credibly proven: in general, an exact tripartition of an angle, only with a compass, pen and unmarked ruler, is not possible. However, it can be an exciting task to find an approximation construction that has the smallest possible absolute error with relatively little effort.
Well, the question: Which approximation construction holds the record?
Here is an example of a approximation construction that has acceptable accuracy with relatively little effort:
https://commons.wikimedia.org/wiki/File:01_Dreiteilung_des_Winkels-180%…