Maths in a minute: Branching processes
Imagine you're looking at a little bacterium in a petri dish. You know that it'll produce anything between 0 and 5 offspring in a day and then die. Each offspring will in turn produce between 0 and 5 offspring in a day and then die. And so on.
Will the population of offspring eventually grow very large, or will it go extinct?
One way to figure out an answer is to model the process using a die. Draw a dot on a piece of paper for the first bacterium. Then roll the die. If it's a 1, there are 0 offspring, if it's a 2 there is one offspring, if it's a 3 there are 2, and so on. You can represent the new offspring (if there are any) by dots in a row below the original dots. Then repeat the process for the new generation of bacteria. Stop when the population has died out, or when it's reached your favourite large number.
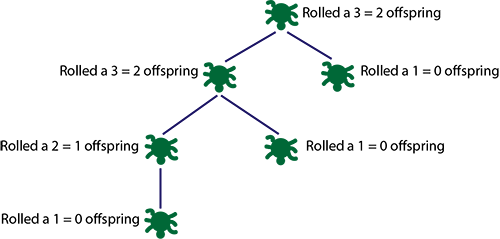
What we have just described is what mathematicians call a branching process. The diagram above illustrates why the word "branch" comes into the picture. A single run of the branching process won't tell you anything about what you can expect to happen to your population of bacteria — it all depends on the rolls of the die. But running it many times (preferably on a computer) can give you an idea of what kind of outcomes are most likely to occur. If the branching process goes extinct (or grows large) in most of your simulations then this is what is likely to happen to the population in your petry dish too.
Mathematicians use probability theory to make this idea more precise and derive interesting information from branching processes. For example, in our example the expected number of offspring per bacterium is 2.5 (you can think of this as an average). You can show mathematically that this means that the expected size of the population at generation n is $2.5^n$. Since this number keeps growing from generation to generation, you can deduce that the population is unlikely to die out (though it could still die out if you happen to roll a lot of 1s).
Mathematicians have also come up with many ways of modifying and extending the basic idea of a branching process we have described here to model more complex processes. For example, we have said that each of the possible outcomes of the roll of the die is equally likely, but we could also have used another probability distribution with some outcomes more likely than others. It is also possible to define a branching process where the length of time until an individual produces offspring or dies varies. Or you could define a branching process in which individuals have different characteristics. Many variations are possible.
Many processes in the world can be modelled using branching processes. An example is the spread of a new disease that has just entered a population. You can't predict with certainty if it'll spread or die out, as a lot depends on the first few people who catch it — whether they pass it on to lots of others or not. Branching processes can help you get some kind of a grip on this uncertainty.
This article is part of our collaboration with JUNIPER, the Joint UNIversities Pandemic and Epidemiological Research network. JUNIPER is a collaborative network of researchers from across the UK who work at the interface between mathematical modelling, infectious disease control and public health policy. You can see more content produced with JUNIPER here.
