
Maths in a minute: Cayley graphs
Imagine you’re trying to solve a Rubik’s cube methodically. To plan out your moves, you might try beginning by writing down your starting position and connecting it to all possible positions which are one move away.
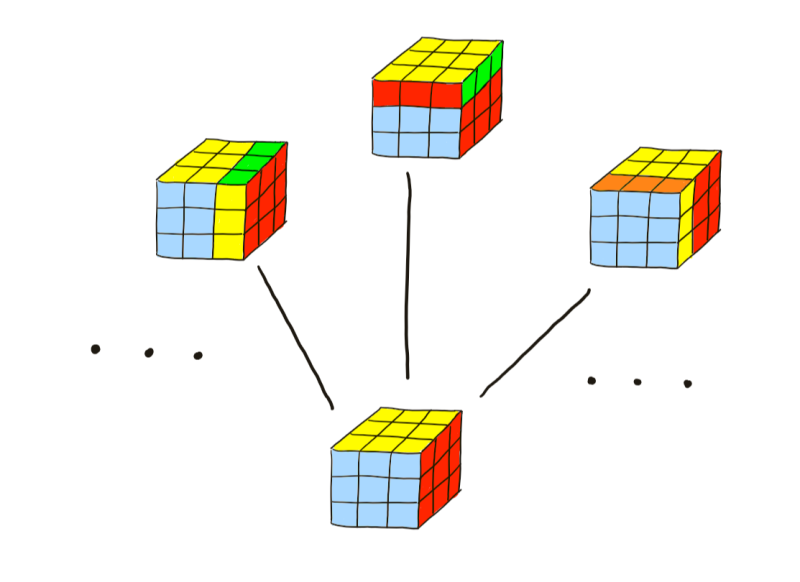
Then, from each of these new positions, you connect them to all possible positions which are one move away.
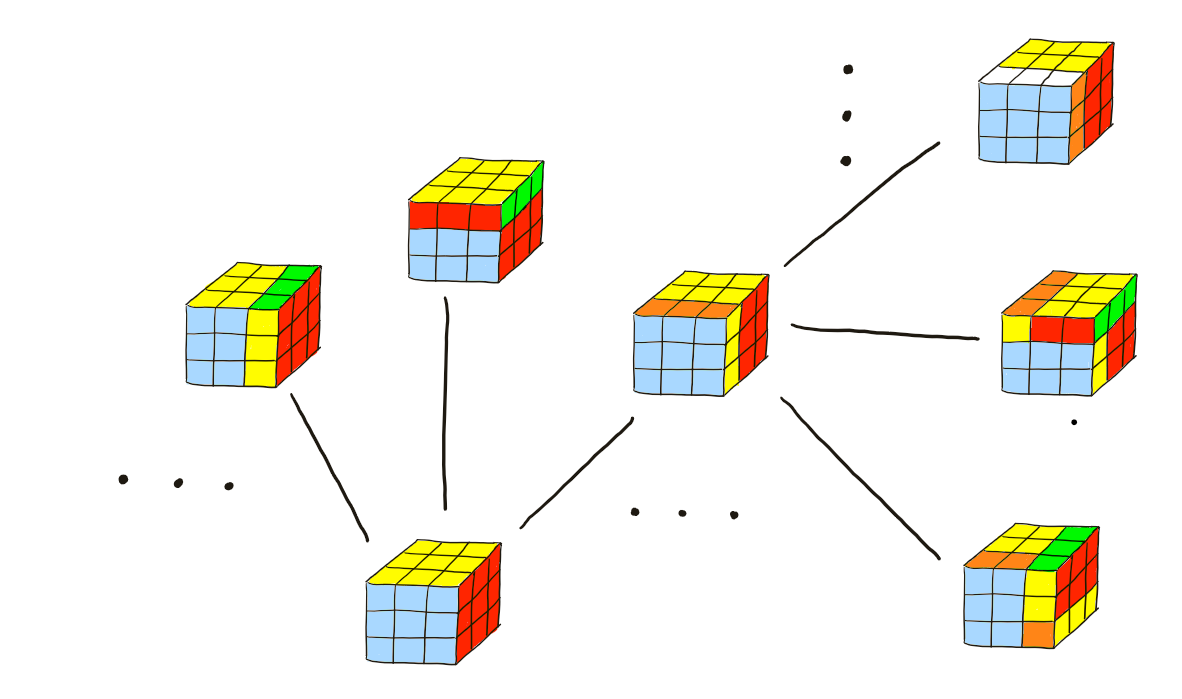
If you do this repeatedly for every possible position of the Rubik’s cube, you’ll have a complete map of all the positions of the Rubik’s cube, as well as paths connecting any position to any other position using only individual moves. Solving a Rubik’s cube is now the same as finding a path in this map which takes you from your starting position to the solved position! Mathematicians call this map a Cayley graph of the group of permutations of the Rubik’s cube.
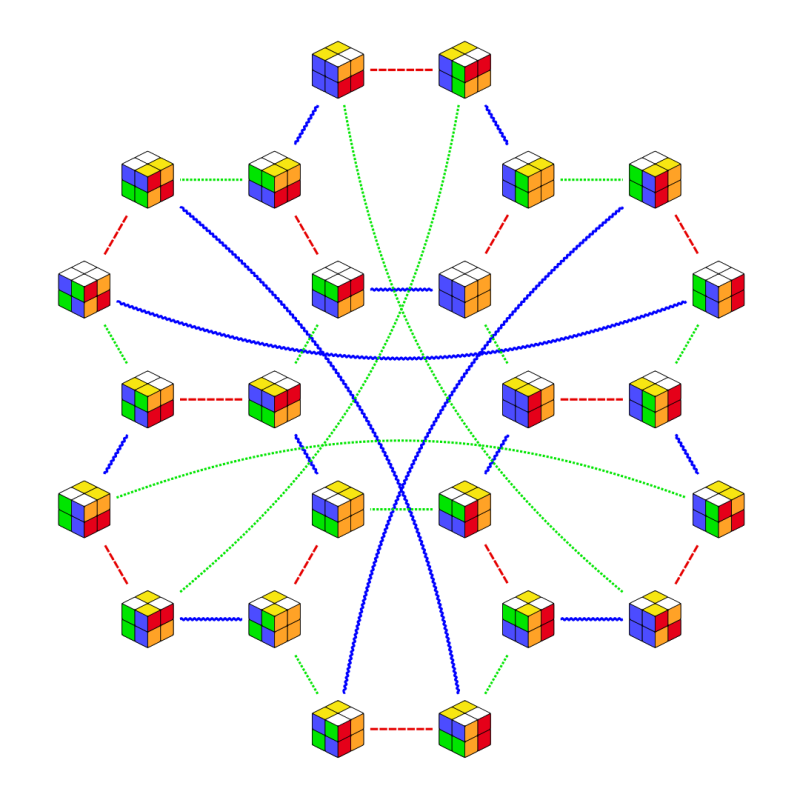

The collection of permutations of a Rubik’s cube is one example of a general mathematical object called a group. We can similarly draw a Cayley graph for any other group. Think of the Cayley graph of a group as a map of all its elements, together with streets along certain allowed directions connecting the different elements.
Formally, given a group, we pick a subset of group elements to act as allowed directions to move in. In the case of a Rubik’s cube, the allowed directions are all the permutations given by rotating at most one face. Then, we construct a graph (a general name for a collection of nodes, called vertices, and edges connecting them) with one vertex for each group element, and connect two vertices with an edge if we can get from the first vertex to the second by left-multiplying by one of the allowed directions. The resulting graph is known as the Cayley graph of the group.
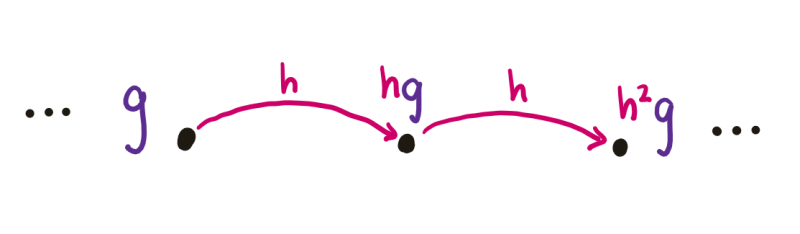
(A technical note: in the case of the Rubik’s cube, the vertices should technically be the set of permutations of the Rubik’s cube. For the sake of the story, we secretly identified each permutation with the position achieved by applying the permutation to the solved cube.)
Notice that if we pick a different set of allowed directions, we’ll get a different Cayley graph. The vertices would still be the elements of the group, but they would be connected in a different way.
Cayley graphs are useful because they turn groups from an algebraic object to a geometric one. For example, they give us a notion of distance in a group. Given a group and a specified set of allowed directions, the distance between two elements in the group is the number of steps we have to take in its Cayley graph to get from the first element to the second. For a Rubik’s cube, the distance between two positions is the number of moves we have to make to get from the first position to the second.
Cayley graphs have given rise to the modern subject of geometric group theory, which draws connections between the algebra of groups and the geometry of their Cayley graphs. For more about this active field of research, see here:
Groups, geometry, and Gromov — Find out about the proof that started the modern field of geometric group theory.