
Maths in a minute: Simplifying circuits
Most of us are aware that the work done by our computers is accomplished by breaking tasks down into a series of just a few logical operations. These operations – AND, OR and NOT – can be physically represented in the computer circuits and mathematically representation using Boolean algebra. (You can read more in Maths in a minute: Boolean algebra.) This realisation of the links between circuitry, logic and algebra was first made by Claude Shannon (1916 - 2001), who in 1936 was a 20-year-old student at Massachusetts Institute of Technology writing his Masters thesis.
Shannon was considering complex circuits of switches and relays that were used in places such as telephone exchanges. Suppose that you have a complicated circuit design, a mess of wires and switches. Shannon realised that if you wrote down the corresponding Boolean algebra expression, you could quickly use the simplification laws to remove redundant components in your circuit.
For example, consider this circuit:
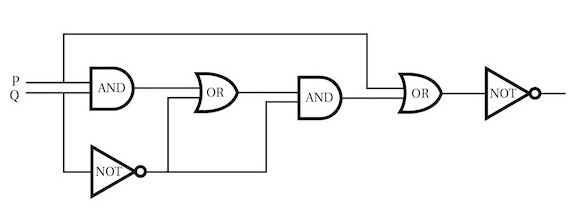
This circuit diagram is written in shorthand with symbols to represent the AND, OR and NOT gates that combine the 0/1 values for P and Q.
The circuit above corresponds to the expression
((P x Q + Q') x Q' + P)'
This expression can be simplified using the laws of Boolean algebra as follows:
| ((P x Q + Q') x Q' + P)' | |
| = ((P x Q + Q') x Q')' x P' | (by De Morgan's laws) |
| =((P x Q + Q')' + Q) x P' | (by De Morgan's laws) |
| =((P x Q)' x Q + Q) x P' | (by De Morgan's laws) |
| = Q x P' | (by the simplification rule A+A x B) |
So analysing the original circuit using Boolean algebra reveals that a simple circuit with just two gates will do the same trick as the original complicated one.
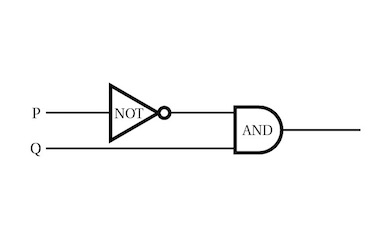
This simple circuit, with just two gates, is equivalent to the original complex one.
Before Shannon's work, simplifying a circuit design involved writing all the possible positions of the switches in the circuit and following through the chain of events for each, a process he himself described as "very tedious and open to errors." But now, thanks to his insight, any circuit could be easily described and simplified using Boolean algebra.