Maths in a minute: Take it to the limit

Sequences of numbers can have limits. For example, the sequence 1, 1/2, 1/3, 1/4, ... has the limit 0 and the sequence 0, 1/2, 2/3, 3/4, 4/5, ... has the limit 1.

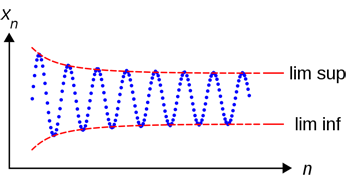
But not all number sequences behave so nicely. For example, the sequence 1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 4/5, ... keeps jumping up and down, rather than getting closer and closer to one particular number. We can, however, discern some sort of limiting behaviour as we move along the sequence: the numbers never become larger than 1 or smaller than 0. And what's more, moving far enough along the sequence, you can find numbers that get as close as you like to both 1 and 0. So both 0 and 1 have some right to be considered limits of the sequence — and indeed they are: 1 is the limit superior and 0 is the limit inferior, so-called for obvious reasons.

But can you define these limits superior and inferior for a general sequence $(a_n) = a_1, a_2, a_3, ...$ , for example the one shown in the picture? Here's how to do it for the limit superior. First look at the whole sequence and find its least upper bound: that's the smallest number that's bigger than all the numbers in the sequence. Then chop off the first number in the sequence, $a_1,$ and again find the least upper bound for the new sequence. This might be smaller than the previous least upper bound (if that was equal to $a_1$), but not bigger. Then chop off the first two numbers and again find the least upper bound.

Keep going, chopping off the first three, four, five, etc numbers, to get a sequence of least upper bounds (indicated by the red curve in the picture). In this sequence every number is either equal to or smaller than the number before. The limit superior is defined to be the limit of these least upper bounds. It always exists: since the sequence of least upper bounds is either constant or decreasing, it will either approach minus infinity or some other finite limit. The limit superior could also be equal to plus infinity, if there are numbers in the sequence that get arbitrarily large.

The limit inferior is defined in a similar way, only that you look at the sequence of greatest lower bounds and then take the limit of that.

You can read more about the limits inferior and superior in the Plus article The Abel Prize 2012.