The design for the new maths gallery

Would you like to step inside an abstract mathematical space? Soon you'll be able to do just that, in the maths gallery at the Science Museum in London, due to open in 2016.

"We decided we should provide an abstract environment," says Shajay Bhooshan from Zaha Hadid Architects, the lead designer on the project. "It's related to mathematics, and not so much to the rest of the museum, but provides a kind of hermetic, contemplative environment."

Inside this experience of the abstract beauty of maths will be examples of its everyday implications that affect us all. The layout of the gallery is based on a simulation of the turbulence field around an experimental plane from 1929 – the Handley Page Gugnunc. "That particular aircraft is one of the first [to be built for] mathematical competitions conducted to make flying safer for commercial and passenger use," says Bhooshan. It was designed for the Guggenheim Safe Aircraft competition in 1929 which aimed to find planes that could fly safely at slow speeds and with short takeoffs. The research behind the plane profoundly advanced aviation technology and understanding at the very beginnings of civilian air travel. (You can read two brilliant articles from the 1930s about the competition and the aircraft itself.)

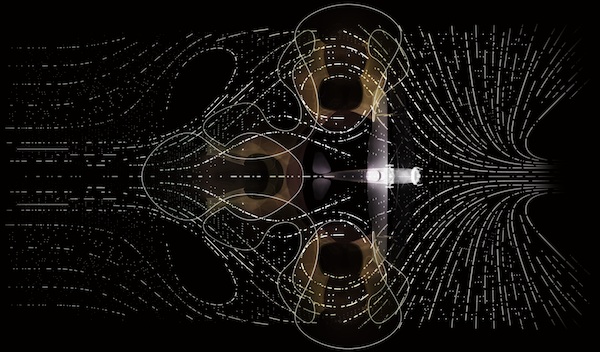
A top view of the turbulence field around the Handley Page aircraft, one of the main exhibits in the new maths gallery (Image courtesy of Zaha Hadid Architects)

Behind the plane will hang three surfaces which all stem from the same mathematical equation, the same equation that gives rise to the huge variety of surfaces that form the plinth for objects throughout the gallery. The equation defining these $$ \begin{array}{l} a_1 sin(x)sin(2y)sin(3z) \\ + a_2 sin(2x)sin(y)sin(3z)\\ +a_3 sin(2x)sin(3y)sin(z)\\ +a_4 sin(3x)sin(y)sin(2z)\\ +a_5 in(x)sin(3y)sin(2z)\\ +a_6sin(3x)sin(2y)sin(z)=0 \end{array} $$ is a complicated looking combination of familiar sine functions that is governed by six different parameters. By varying the values of these parameters, the $a_i$, the surface bends and twists producing a whole family of different shapes. Some of these will be created in physical form to provide the support display cases used throughout the galleries.

All of the shapes within the display cases in the gallery have been produced from a single equation. You can play with these surfaces yourself or watch their creation in the video below.

The project has had a particular resonance for Bhooshan and his colleagues as maths has become an essential part of the toolkit for designers today. "I don't have a formal background in mathematics, but I've grown with the company for the last seven years, and as the design process has got more complex, we've learned some of the maths that makes our lives easier," says Bhooshan. "Day in and day out, a lot of our work is writing little apps or applets to explore geometry and how it can be optimised for multiple criteria, such as spatial, aesthetic, fabrication or structural criteria. We are writing code, and of course code is just a way of manifesting the mathematics behind all of these things."

The final design of the gallery has an elegance and simplicity that echoes the beauty of a mathematical proof. "The end result seems simple," says Bhooshan. "That's the most satisfying thing, [given] all the effort that goes into making it simple and tangible." And mathematics will no doubt continue to play a part in the building of the gallery. "I'm sure there will be many more instances where maths and physics will come to the foreground in the process of designing it and getting it made." It seems fitting that the new gallery will not only contain mathematical objects telling mathematical stories, but the very fabric of it will be built from maths. We can't wait to visit!