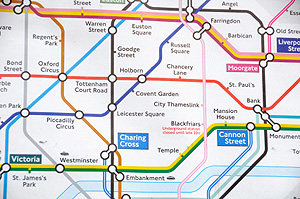A piece of a geographically accurate map of the London Underground (top, image from Wikimedia commons) and the (roughly) corresponding piece of the network on the actual map (bottom).

The world of computer science is buzzing with reports of exciting news. It involves networks: those potentially complex beasts we all encounter every day, in the form of the internet, or the social, transport and utility networks we depend upon. The problem is that the same network can appear in different guises — which prompts the question of how hard it is to tell whether two apparently different networks are actually the same. László Babai, a mathematician and computer scientist at the University of Chicago in Illinois, claims he can prove it's not as hard as some people had thought. If he is correct then, according to the computer scientist Scott Aaronson writing on his blog, this would constitute the "theoretical computer science result of the decade".

We often think about networks as anchored in space. A map of a train network, for example, overlays the geographical map of the region it is in. But there is more than one way in which you can represent a network in space. The London Underground map is a great example of this. The relative locations of the stations have been changed, compared to the geographical map, to make it easier to read (find out more here). Another example are the two pictures shown below on the left. Despite their appearance, they represent the same network: by moving the nodes around you can turn one network into the other so that the links between nodes exactly match.

Abstractly, a network is just a collection of nodes linked up in a certain way. The question that has been bugging computer scientists is not whether they can spot if two networks, given by different representations, are the same. They have algorithms, step-by-step recipes, which can do just that. Rather, they have been wondering whether there's an algorithm that is faster than the ones they know of.

It's obvious that the problem becomes harder as the networks in question grow larger. There are many other problems that display the same feature. Examples are searching an unordered list for a particular entry, or factoring a number: the larger the list or the number, the longer it will take an algorithm to come up with the answer.

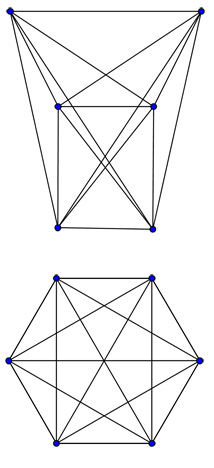
Both of these networks consist of six nodes with each node connected to all the other nodes.

Computer scientists classify problems by seeing how fast the time it takes to solve them grows with the size of the input. For example, suppose the size of the input (the size of the list to be searched or number to be factored) is $n.$ If the time it takes to solve the problem grows roughly like $n,$ or $n^2,$ or $n^3,$ or $n^k$ for any other natural number $k,$ as $n$ gets larger, then the problem is deemed "easy". The number $n^k$ could still grow fast with $n$ if $k$ is large, of course, but this kind of polynomial growth, as it's called, is nowhere near as explosive as exponential growth, described, for example, by the expression $2^n$. (See here for a more technical definition of so-called polynomial time algorithms.)

Babai claims to have shown that the network problem (telling whether two networks are the same) can be solved by an algorithm that is nearly, but not quite, as fast as the polynomial time algorithms that characterise the "easy" problems. This means that the problem isn't as hard as people had previously thought.

Why is this result important? You might think it's for practical reasons: because it gives people dealing with large networks, such as the internet, a much longed-for tool for solving some of their problems faster. But this isn't the case. People have long known of algorithms that efficiently solve the network problem for the vast majority of networks they come across in the real world. Babai's result is important for purely theoretical reasons: it represents a rare type of progress in an area called complexity theory.

Using the run time of algorithms, complexity theorists have come up with a hierarchy of complexity classes. The "easy" problems, those for which the time grows polynomially with the input, belong to a class called P. Then there is a class called NP. It consists of problems that may not be as easy to solve as the P ones, but for which a potential solution is easily verified. The problem of spotting whether two networks are the same belongs to the NP class: if someone tells you how one network can be transformed into another, or gives you a reason for why it can't, then it's easy to check whether they are correct (to be precise, a potential solution to an NP problem can be checked in polynomial time). Within the NP class there's a class of problems thought to be particularly hard, known as NP complete problems. (There are also other complexity classes, but we'll ignore them here.)

This all seems very neat, but as it turns out, the stack of complexity classes is shrouded in mystery. For a start, there's an embarrassing gap in the middle. While complexity theorists have many examples of problems that belong in the NP complete class and many examples of problems that belong in the P class, they know of only few problems that appear to fall in between: too hard to be in P and too easy to be NP complete. More dramatically, there may not even be a middle. NP problems are thought to be hard because nobody knows any polynomial-time algorithm to solve them. But this doesn't mean that such algorithms don't exist. If someone discovers such algorithms, then the NP class will simply collapse, as all those supposedly hard NP problems end up in the "easy" P class after all. As a computer science expert recently admitted to us, the embarrassing fact about complexity theory is that nearly nothing is known for certain (in fact, you could win a million dollars for settling the P versus NP problem).

This is why the network problem is so interesting to complexity theorists. It's a firm candidate for a problem that belongs to the elusive middle class between P and NP complete problems. Babai's result narrows down the location of the network problem within this supposed middle class: it's just above, though not quite in, the "easy" P class. There are a range of other problems that can be reduced to the network problem, and Babai's claim implies that these too are just above P. Results that reduce the complexity of important problems are rare, and so they are always a cause for celebration.

Babai's result doesn't rule out the possibility that someone may still find a polynomial time algorithm to solve the network problem, putting it squarely in the P class. Some will no doubt take Babai's success as an indication that the P class is indeed where the problem belongs, or even indulge in speculations that other problems may also slide down the complexity hierarchy and that the P and NP classes will eventually turn out to be the same. But others will read the result the other way. If even an enormous amount of work hasn't succeeded in squeezing the problem into the P class, then maybe that's because it doesn't belong there. It will probably be quite a while until complexity theorists find the answer. To start with they will need to confirm that Babai's result really is correct.

We would like to thank Colva Roney-Dougal of St. Andrew's University for guiding us safely through the puzzling thicket of complexity classes.