
Mysterious number 6174

Anyone can uncover the mystery
The number 6174 is a really mysterious number. At first glance, it might not seem so obvious. But as we are about to see, anyone who can subtract can uncover the mystery that makes 6174 so special.
Kaprekar's operation
In 1949 the mathematician D. R. Kaprekar from Devlali, India, devised a process now known as Kaprekar's operation. First choose a four digit number where the digits are not all the same (that is not 1111, 2222,...). Then rearrange the digits to get the largest and smallest numbers these digits can make. Finally, subtract the smallest number from the largest to get a new number, and carry on repeating the operation for each new number.
It is a simple operation, but Kaprekar discovered it led to a surprising result. Let's try it out, starting with the number 2005, the digits of last year. The maximum number we can make with these digits is 5200, and the minimum is 0025 or 25 (if one or more of the digits is zero, embed these in the left hand side of the minimum number). The subtractions are:
5200 - 0025 = 5175
7551 - 1557 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
When we reach 6174 the operation repeats itself, returning 6174 every time. We call the number 6174 a kernel of this operation. So 6174 is a kernel for Kaprekar's operation, but is this as special as 6174 gets? Well not only is 6174 the only kernel for the operation, it also has one more surprise up its sleeve. Let's try again starting with a different number, say 1789.
9871 - 1789 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
We reached 6174 again!

A very mysterious number...
When we started with 2005 the process reached 6174 in seven steps, and for 1789 in three steps. In fact, you reach 6174 for all four digit numbers that don't have all the digits the same. It's marvellous, isn't it? Kaprekar's operation is so simple but uncovers such an interesting result. And this will become even more intriguing when we think about the reason why all four digit numbers reach this mysterious number 6174.
Only 6174?
The digits of any four digit number can be arranged into a maximum number by putting the digits in descending order, and a minimum number by putting them in ascending order. So for four digits a,b,c,d where
9 ≥ a ≥ b ≥ c ≥ d ≥ 0
and a, b, c, d are not all the same digit, the maximum number is abcd and the minimum is dcba.
We can calculate the result of Kaprekar's operation using the standard method of subtraction applied to each column of this problem:
| a | b | c | d | |
| - | d | c | b | a |
|
|
||||
|---|---|---|---|---|
| A | B | C | D | |
which gives the relations
| D = 10 + d - a (as a > d) |
| C = 10 + c - 1 - b = 9 + c - b (as b > c - 1) |
| B = b - 1 - c (as b > c) |
| A = a - d |
for those numbers where a>b>c>d.
A number will be repeated under Kaprekar's operation if the resulting number ABCD can be written using the initial four digits a,b,c and d. So we can find the kernels of Kaprekar's operation by considering all the possible combinations of {a, b, c, d} and checking if they satisfy the relations above. Each of the 4! = 24 combinations gives a system of four simultaneous equations with four unknowns, so we should be able to solve this system for a, b, c and d.
It turns out that only one of these combinations has integer solutions that satisfy 9 ≥ a ≥ b ≥ c ≥ d ≥ 0. That combination is ABCD = bdac, and the solution to the simultaneous equations is a=7, b=6, c=4 and d=1. That is ABCD = 6174. There are no valid solutions to the simultaneous equations resulting from some of the digits in {a,b,c,d} being equal. Therefore the number 6174 is the only number unchanged by Kaprekar's operation — our mysterious number is unique.
For three digit numbers the same phenomenon occurs. For example applying Kaprekar's operation to the three digit number 753 gives the following:
753 - 357 = 396
963 - 369 = 594
954 - 459 = 495
954 - 459 = 495
The number 495 is the unique kernel for the operation on three digit numbers, and all three digit numbers reach 495 using the operation. Why don't you check it yourself?
How fast to 6174?
It was about 1975 when I first heard about the number 6174 from a friend, and I was very impressed at the time. I thought that it would be easy to prove why this phenomenon occurred but I could not actually find the reason why. I used a computer to check whether all four digit numbers reached the kernel 6174 in a limited number of steps. The program, which was about 50 statements in Visual Basic, checked all of 8991 four digit numbers from 1000 to 9999 where the digits were not all the same.
The table below shows the results: every four digit number where the digits aren't all equal reaches 6174 under Kaprekar's process, and in at most seven steps. If you do not reach 6174 after using Kaprekar's operation seven times, then you have made a mistake in your calculations and should try it again!
| Iteration | Frequency |
|---|---|
| 0 | 1 |
| 1 | 356 |
| 2 | 519 |
| 3 | 2124 |
| 4 | 1124 |
| 5 | 1379 |
| 6 | 1508 |
| 7 | 1980 |
Which way to 6174?
My computer program checked all 8991 numbers, but in his article Malcolm Lines explains that it is enough to check only 30 of all the possible four digit numbers when investigating Kaprekar's operation.
As before let's suppose that the four digit number is abcd, where
9 ≥ a ≥ b ≥ c ≥ d ≥ 0.
Let us calculate the first subtraction in the process. The maximum number is 1000a+100b+10c+d and the minimum number is 1000d+100c+10b+a. So the subtraction is:
1000a + 100b + 10c + d - (1000d + 100c + 10b + a)
= 1000(a-d) + 100(b-c) + 10(c-b) + (d-a)
= 999(a-d) + 90(b-c)
The possible value of (a-d) is from 1 to 9, and (b-c) is from 0 to 9. By running through all the possibilities, we can see all the possible results from the first subtraction in the process. These are shown in Table 1.
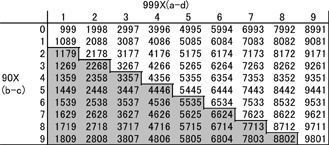
Table 1: Numbers after the first subtraction in Kaprekar's process
We are only interested in numbers where the digits are not all equal and
a ≥ b ≥ c ≥ d,
therefore we only need to consider those where (a-d) ≥ (b-c). So we can ignore the grey region in Table 1 which contains those numbers where
(a-d) < (b-c).
Now we arrange the digits of the numbers in the table in descending order, to get the maximum number ready for the second subtraction:
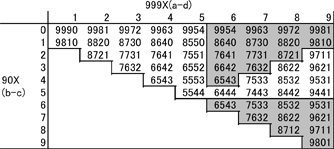
Table 2: Maximum numbers, ready for the second subtraction
We can ignore the duplicates in Table 2 (the grey regions), and are left with just 30 numbers to follow through the rest of the process. The following figure shows the routes which these numbers take to reach 6174.
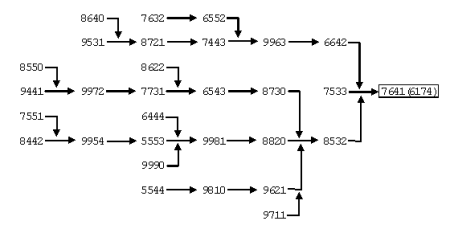
How these 30 numbers reach 6174
From this figure you can see how all the four digit numbers reach 6174 and reach it in at most seven steps. Even so I still think it is very mysterious. I guess Kaprekar, who discovered this number, was extremely clever or had a lot of time to think about it!
Two digits, five digits, six and beyond...
We have seen that four and three digit numbers reach a unique kernel, but how about other numbers? It turns out that the answers for those is not quite as impressive. Let try it out for a two digit number, say 28:
82 - 28 = 54
54 - 45 = 9
90 - 09 = 81
81 - 18 = 63
63 - 36 = 27
72 - 27 = 45
54 - 45 = 9
It doesn't take long to check that all two digit numbers will reach the loop 9→81→63→27→45→9. Unlike for three and four digit numbers, there is no unique kernel for two digit numbers.
But what about five digits? Is there a kernel for five digit numbers like 6174 and 495? To answer this we would need to use a similar process as before: check the 120 combinations of {a,b,c,d,e} for ABCDE such that
9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0
and
abcde - edcba = ABCDE.
Thankfully the calculations have already been done by a computer, and it is known that there is no kernel for Kaprekar's operation on five digit numbers. But all five digit numbers do reach one of the following three loops:
71973→83952→74943→62964→71973
75933→63954→61974→82962→75933
59994→53955→59994
As Malcolm Lines points out in his article, it will take a lot of time to check what happens for six or more digits, and this work becomes extremely dull! To save you from this fate, the following table shows the kernels for two digit to ten digit numbers (for more see Mathews Archive of Recreational Mathematics). It appears that Kaprekar's operation takes every number to a unique kernel only for three and four digit numbers.
| Digits | Kernel |
|---|---|
| 2 | None |
| 3 | 495 |
| 4 | 6174 |
| 5 | None |
| 6 | 549945, 631764 |
| 7 | None |
| 8 | 63317664, 97508421 |
| 9 | 554999445, 864197532 |
| 10 | 6333176664, 9753086421, 9975084201 |
Beautiful, but is it special?
We have seen that all three digit numbers reach 495, and all four digit numbers reach 6174 under Kaprekar's operation. But I have not explained why all such numbers reach a unique kernel. Is this phenomenon incidental, or is there some deeper mathematical reason why this happens? Beautiful and mysterious as the result is, it might just be incidental.
Let's stop and consider a beautiful puzzle by Yukio Yamamoto in Japan.
If you multiply two five digit numbers you can get the answer 123456789. Can you guess the two five digit numbers?
This is a very beautiful puzzle and you might think that a big mathematical theory should be hidden behind it. But in fact it's beauty is only incidental, there are other very similar, but not so beautiful, examples. Such as:
(We can give you a hint to help you solve these puzzles, and here are the answers.)
If I showed you Yamamoto's puzzle you would be inspired to solve it because it is so beautiful, but if I showed you the second puzzle you might not be interested at all. I think Kaprekar's problem is like Yamamoto's number guessing puzzle. We are drawn to both because they are so beautiful. And because they are so beautiful we feel there must be something more to them when in fact their beauty may just be incidental. Such misunderstandings have led to developments in mathematics and science in the past.
Is it enough to know all four digit numbers reach 6174 by Kaprekar's operation, but not know the reason why? So far, nobody has been able to say that all numbers reaching a unique kernel for three and four digit numbers is an incidental phenomenon. This property seems so surprising it leads us to expect that a big theorem in number theory hides behind it. If we can answer this question we could find this is just a beautiful misunderstanding, but we hope not.
Note from the editors: many readers noticed that repeatedly adding up the digits of any of the kernels of Kaprekar's operation always equals 9. Find out why in this follow-up to the article.
References
- Kaprekar, D. R., "Another Solitaire Game", Scripta Mathematica, vol 15, pp 244-245 (1949)
- Gardner, Martin, "The Magic Numbers of Doctor Matrix", Japanese version, Tokyo: Kinokuniya (1978)
- Lines, Malcolm E., A number for your thoughts: facts and speculations about numbers..., Bristol: Hilger (1986)
- Nishiyama, Yutaka, Kurashi no Algorithm, Kyoto: Nakanishiya (1993)
About the author

Yutaka Nishiyama is a professor at Osaka University of Economics, Japan. After studying mathematics at the University of Kyoto he went on to work for IBM Japan for 14 years. He is interested in the mathematics that occurs in daily life, and has written seven books about the subject. The most recent one, called "The mystery of five in nature", investigates, amongst other things, why many flowers have five petals. Professor Nishiyama is currently visiting the University of Cambridge.
Comments
Anonymous
visual basic didn't exist in 1975
Anonymous
Yes, visual basic didn't exist in 1975.
I tested it by FORTRAN program in those days and recently test again by visual basic or visual studio.
Yutaka Nishiyama
Anonymous
I almost stopped reading and left the page at the point you seemed to imply that in 1975 there was extant visual basic. I am so glad I kept on reading.
Anonymous
Thank you for taking the time to put all this together. A very interesting read, I appreciate the time you took to make it. Nice pictures and diagrams too!
Anonymous
BASIC was the programming taught to me in High School 1974, with a audio coupler, teletype & papertape....
Richard Claessens
Yes I also learned basic in fact I learned MS-DOS and basic about the same time I later went on to try and understand C++. Let you in college but had difficulty with the arrays I probably should have studied Fortran first
Anonymous
I'd like to see what happens to 11-20 digit numbers. What is the limit for which the kernel has been found? thank you
Anonymous
Hi
Have they missed something about the 495 being a kernel for 3 digits only?
You get this number from 4 digits as well
try any 4 digit number in pairs divided by one another for example 5858 or 1919 and then deduct 5588 or 1199 and u will get to 495 in not time
Vishal Agarwal
As you said: try with 5858 or 1919
8855-5588= 3267
7632-2367 = 5265
6552-2556 = 3996
9963-3699 = 6264
6642-2466 = 4176
7841-1467 = 6714
Anonymous
In Mathematica. But no kernels found :(
ClearAll["Global`*"]
Manipulate[
num = 10^n - 2;
t = Table[
num = (num // IntegerDigits // Sort // Reverse //
FromDigits)*(10^((n - (num // Log10)) // Floor)) - (num //
IntegerDigits // Sort // FromDigits), {x, 0, 50}] //
ListPlot, {n, 2, 40, 1}]
Anonymous
... also, has there been any investigation as to why the digits need to be different? Clearly, this works for some numbers with repeating digits, eg
9871 - 1789 = 8082 -> since 9871 reaches 6174 so much 8082
thank you
Anonymous
The criteria wasn't "no repeating" digits -- just " not all repeating." In other words, you can't use 1111,2222,3333,4444,5555,6666,7777,8888, or 9999 for obvious reasons (the largest and smallest numbers would be the same and so the first subtraction would yield zero). But any other 4-digit combination should work -- so 1112 or 1311 or whatever would be fine.
quantumness
Actually 1112 doesn’t work:
2111-1112 = 999
folke
Actually 1112 does work:
2111-1112 = 999
9990 - 0999 =
...
8532 - 2358 = 6174
5 iterations.
Anonymous
Hi
You also get 495 from any 4 digit number made of pairs for example 1919 and then deducting 1199 you get to 6174 in not time so I dont see any wonder on this!
The wonder I see is you swap this digits by starting with the higher number in front example 9191 -deducting 1199 and you end up with 6174:))))
SHAKEEL
9911-1199=8712
8721-1278=7443
7443-3447=3996
9963-3699=6264
6642-2466=4176
7641-1467=6174
Anonymous
Very nice article, I enjoyed it
(who cares whether visual basic existed in 1975 or not)
Chuck N.
I care. And people like me who were into programming in the 70s care. But the author explained his slip, above.
I taught math and programming through the 70s, 80s, and 90s. This is the first time I ran into this number pattern. Thanks for a fine presentation.
Anonymous
What happens if this experiment is repeated with different bases such as octal (0-7) hex (0-f) or binarry (0,1)?
Anonymous
I also saw the VB error but it did not detract from the subject in anyway. Again thanks for sharing.
Anonymous
Very nice article.
For a non mathematician, I struggled for quite a while through the 4 lines of relations (e.g. trying to figure out how b had to be greater than c for the third one), it was only later that I read 'for those numbers where a>b>c>d'. Maybe that should go first?
Also am curious about how the iterations play out in non decimal bases?
Thanks!
Anonymous
Is it true that every number of digits that is a prime number has no kernel? Like, will a number of 11 digits have a "None"?
Anonymous
No, it is not. Three is a prime, and has a kernel.
veeraswami
3 is the only odd prime that is related to 9 by virtue of it being its divisor. All subsequent primes don't have any correlation with 9. Just the test on 11 will tell us by means of falsification if the hypothesis holds good.
Anonymous
More mystery or am I just making it up? The digits 6172 "appears" in the list of kernels for all numbers with a length which is even (greater than 3), 6174 for 4 digits, 631764 for 6 digits, 63317664 for 8 digits and 6333176664 for 10 digits. Does this mean 633331766664 is a possible kernel for numbers with 12 digits?
Anonymous
Yes.
Anonymous
There's an interesting fact about the 10-digit kernels, if you try looping '1234567890' around it also comes back!
Anonymous
Hi there,
How does your calculation work?
I see your result:
Iteration Frequency
0 1
1 356
2 519
3 2124
4 1124
5 1379
6 1508
7 1980
But, my test gives:
[0] => 1
[1] => 356
[2] => 519
[3] => 2124
[4] => 1124
[5] => 1311
[6] => 1508
[7] => 1980
[10] => 68
See the difference on the 5th iteration. When I look back, this resulted from the following digits:
1000,1011,1101,1110,1112,1121,1211,1222,2111,2122,2212,2221,2223,2232
,2322,2333,3222,3233,3323,3332,3334,3343,3433,3444,4333,4344,4434,4443
,4445,4454,4544,4555,5444,5455,5545,5554,5556,5565,5655,5666,6555,6566
,6656,6665,6667,6676,6766,6777,7666,7677,7767,7776,7778,7787,7877,7888
,8777,8788,8878,8887,8889,8898,8988,8999,9888,9899,9989,9998
A random test with 3433 gives:
#1: 4333 - 3334 = 999
#2: 999 - 999 = 0
#3: 0 - 0 = 0
#4: 0 - 0 = 0
#5: 0 - 0 = 0
#6: 0 - 0 = 0
#7: 0 - 0 = 0
#8: 0 - 0 = 0
#9: 0 - 0 = 0
#10: 0 - 0 = 0
Can you clarify this? Maybe my calculations are wrong.
Thank you.
@ariefbayu
Anonymous
Your step #2 is incorrect. The result from step #1 is 0999. So step #2 should be 9990 - 0999 = 8991. If you continue on from there, you'll see that it works out.
Anonymous
999 should be 9990 and 0999 there must be 4 digits in order for it to work. your #2 only has 3 digits.
Anonymous
#2: 999 - 999 = 0 <---- 0999 - 9990 = 8991
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174
7641 - 1467 = 6174 :)
my bast regards
maher - Saleh
ifallah
Anonymous
4333 - 3334 = 999 is correct but need to keep 4 digits so write 0999
then you get:
9990-0999=8991 and so on.
Khelly Lykke
To the 999, one must add the zero. This is a four digit solution not a there digit solution. 9990, 0999
Anonymous
Though mathematics is not my forte I found your artical interesting. As a Forester I was drawn to your the title of your book "The mystry of five in nature". My mind went to the biology term- 'Contact Parastikeits' (spelling may be off) which follows Fibonaccis sequence 1,1,2,3,5,8... Have you found the "Mystery" to follow this sequence?
Dave Peckham
Marianne
Hi Dave,
You can find out more about the Fibonacci sequence here: http://plus.maths.org/content/life-and-numbers-fibonacci-0
Anonymous
Article about Five Petals is there,
http://www.osaka-ue.ac.jp/zemi/nishiyama/math2010kr/five.pdf
http://www.osaka-ue.ac.jp/zemi/nishiyama/index.HTML
My approach is without Fibonaccis sequence.
Yutaka Nishiyama
Anonymous
Hello, when i was playing with numbers. i played with 2 digit numbers and i saw that always, or at least the many times i have done it. i came to a number that is a multypile of 9. is it true or i just got lucky?
Anonymous
The difference between 2 numbers wil the same digits will always be a multiple of 9.
Consider a 2 digit number as 10x + y. Transpose the digits; 10y + x. (10x + y) - (10y + x) = 9x - 9y.
Anonymous
that is true!
Anonymous
your result really works and it was intersting to see
Anonymous
for six digit numbers, you may get into an infinite loop. Try 851742
875421 - 124578 = 750843
875430 - 34578 = 840852
885420 - 24588 = 860832
886320 - 23688 = 862632
866322 - 223668 = 642654
665442 - 244566 = 420876
876420 - 24678 = 851742
Anonymous
What happens when the base is changed? Do we get different solutions for different number of digits?
Anonymous
This is essentially the Fibonacci sequence with the decimal place moved over to the right one time.
Anonymous
All the Kaprekar kernels or kernel loop-numbers are multiples of 9.
Anonymous
For all Kaprekar's constants with an even number of digits, the average of the digits in that number is ALWAYS 4.5!
Anonymous
9*9= 81 ; 8+1 = 9!
45*45= 2025 ; 20 +25 = 45 !
55*55 = 3025 ; 30 + 25 = 55!
99*99= 9801 ; 98+01 = 99!
703*703= 494209 ; 494+209= 703!
5292*5292 = 28005264 ; 28+ 005264 = 5292!
This magic can also be seen on 2728, 857143 etc...
Anonymous
using numbers 0-9 and letters a-z what is the breakdown and mathematical structure for this. Im good at math just not on a deep level like this. Please help. tb205700@aol.com contact me
Anonymous
Dear Readers,
I've just published new book entitled "The Mysterious Number 6174: One of 30 Amazing Mathematical Topics in Daily Life,"
ISBN 978-4768761748.
Please check it at Amazon Japan, and my website is at
http://www.osaka-ue.ac.jp/zemi/nishiyama/index.html
Prof. Yutaka Nishiyama
Shrinath Tandur
Hey, I like how you've managed to put in 6174 into the ISBN number!
Anonymous
every one of the kernels is divisible by 9.