Infinity: A very short introduction

by Ian Stewart

This is a very small book about a, potentially, very large subject. People have been thinking about infinity for a very long time, and there are various angles from which to look at it: religious, philosophical, mathematical. In this book Stewart focusses on the maths, dipping into those bits of philosophy and religion that are relevant. With this tight focus, Stewart has turned what must have seemed like a daunting project into an entertaining, illuminating, and digestible read.

As Stewart points out in the very first sentence of the book, infinity is paradoxical. Perhaps the strangest thing about it is that, despite never actually experiencing anything truly infinite, we all have an intuitive feel for what infinity is. It's something that characterises things that never end, like the counting numbers 1, 2, 3, ..., or a never-ending Universe. Stewart suggests that infinity is a "mental default, a natural side effect of our pattern spotting abilities of our minds". When there's no obvious end to something, such as a piece of line, or the extent of the Universe, we simply assume that there is no end. It's the simplest extrapolation of them all. It's an idea that threads its way through the book: in maths, rolling with our intuitive grasp of infinities can even make things simpler. But it does come at a price.

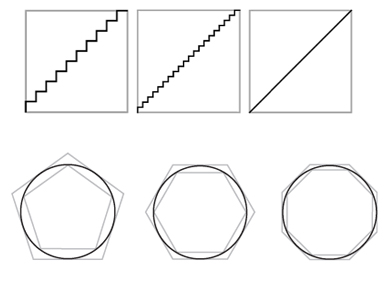
The top diagram shows how the staircases approach the diagonal of the square when the length of the line segments is made smaller. (Image from Infinity: A very short introduction.) The bottom diagram shows how polygons can be used to approximate the area of a circle.

Stewart starts the book with a collection of puzzles, paradoxes and proofs, which will convince you, very quickly, that infinity is tricky. Look at the staircases in the squares in the top diagram on the right, for example. If the length of the square's sides are 1, then the total length of each staircase, including horizontal and vertical bits, is 2: the vertical bits add up to one side of the square and so do the horizontal bits. If you increase the number of steps, by decreasing the length of the bits, then the sequence of staircases approximates the diagonal of the square to any desired degree of accuracy. The natural conclusion is that the length of the diagonal is 2, which is false: it's the square root of 2. Yet in other situations, such an approximation process does give the right answer. For example, you can use a sequence of approximating polygons to work out the area of a circle, as shown in bottom diagram of the figure. Whatever you do with infinity, you need to be careful.

Yet, infinity lurks in many places, as Stewart illustrates in the following chapter. Numbers and their arithmetic is an obvious one, but to begin with Stewart takes us, not all the way to the end of the number line, but into its microscopic structure: decimal expansions, irrational numbers, and the uneasy existence of the rational numbers: even within the smallest segment of the number line you'll find infinitely many rationals, yet they don't join up to form a continuum. It's an easy-going start, but one that already contains plenty of mathematical depth.

A chapter on the history of infinity contains, among things like Zeno's famous paradoxes, Anselm of Canterbury's perplexing proof of the existence of god: "Consider the most perfect being. Since a being that exists is more perfect than a being that does not, the most perfect possible being must exist." The idea that god is perfect also implies that god has no limitations; that he's infinite. Nice try, but the argument is a logical fallacy, and there's a mathematical analogue: similar reasoning can lead you to conclude that the largest number of all numbers is 1 (assume that x is the largest number and that it's bigger than 1 and think about x² - or buy the book).

The philosopher Immanuel Kant attacked Anselm's dodgy reasoning, but made a more sophisticated error of his own. Kant believed that we're all born with an internal representation of space, which we need to understand the physical world. That space is the Euclidean space of straight lines, planes and spaces we learn about at school, complete with its infinite extent and infinite divisibility. Kant thought that Euclidean geometry was both universal and necessary. He was proved wrong on both counts. It's that intuition again: both useful (no one could claim that Euclidean geometry is useless) and misleading.

After the brief but interesting history lesson, Stewart takes us into the worlds of calculus, geometry and physics. The chapter on calculus contains a nice and concise description of the struggle to turn infinitely small and mathematically suspect quantities called infinitesimals into the well-behaved limits most of us struggled with at school. The chapter on geometry has a lesson on perspective drawing and how an artist's natural desire to turn the horizon into a straight line leads to projective geometry. The chapter on physics asks whether real infinites, actual infinities to use Aristotle's language, do exist in the physical world, for example at the centre of black holes. It's the chapter I'd most like to have been longer and more detailed, but there's only so much you can expect from a very short introduction.

The final chapter closes the circle by going back to numbers. It explores Georg Cantor's shocking discovery of an infinity of infinities, one larger than the other, the smallest one being that of the natural numbers. The discovery scandalised some mathematicians of the time (Cantor was called a scientific charlatan and corrupter of youth) but has now found full acceptance. And despite its awe-inspiring nature, Cantor's discovery, or at least some of it, can easily be understood even by newcomers, at least under Stewart's capable instruction.

On the whole, the book has something for everyone. A little mathematical background would be helpful, but even without it there are plenty of interesting insights to take away from the book. Seasoned mathematicians will also enjoy it, as Stewart doesn't cherry pick only the obvious and friendly aspects of the topic. The chapter on calculus has a nice section on non-standard analysis, and I particularly liked the description of Cantor's motivation for thinking about infinity: the infinite sets of zeroes of the trigonometric series that arise in Fourier analysis. The chapter on Cantor also delves into set theory.

Stewart also points out that we could, in theory, do without infinity. "Absolutely no activities that depend on numbers, in the whole of human history, would change if we had limited ourselves to [a] finite range of numbers," he admits. Mathematicians have even devised a version of arithmetic in which there's a very big largest number, but it's clumsy and awkward to work with. And anyway, who would want to do away with such a beautiful and intriguing concept as infinity? I'm pretty sure that anyone who has read this book won't.

Book details:

Infinity: A very short introduction

Ian Stewart

paperback — 160 pages

Oxford University Press (2017)

ISBN 978-0198755234