Nine points will do
To show that, even with only nine points, there must be either a blue triangle or four points connected by red lines, we need a subtle improvement on the reasoning we used for 10 points.
With 10 points, the proof relied on finding a point connected either to at least six red lines, or to at least four blue ones. Once we had such a point, we could be sure to find our three friends or four strangers. And in fact, by counting the lines meeting at a point, we saw that any point would do.
If the graph has only 9 points, each has only 8 neighbours. How can our theorem fail? Only if every point has exactly five red lines and three blue ones. That is, every point must look like this:
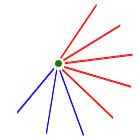
How many blue lines would this annoying graph have? Well, every line has two ends, and three blue lines meet at each of the 9 points. So the total number of blue lines is (9×3)/2, which is 13.5. Oh dear! This is impossible - of course there must be a whole number of blue lines in the graph.
So there must, after all, be at least one point connected to either four blue lines or six red lines, and now the same argument as before shows there must be three friends (a blue triangle) or four strangers.