
Unreasonable effectiveness
Mario Livio's book, Is God a mathematician is reviewed in this issue of Plus.
In 1960, physics Nobel Laureate Eugene Wigner wrote a famous article entitled The Unreasonable Effectiveness of Mathematics in the Natural Sciences. In this article, Wigner referred to the uncanny ability of mathematics not only to describe, but even to predict phenomena in the physical world. He wrote:

Unreasonable effectiveness: how come mathematics describes nature's mysteries so well? This image shows the Orion Nebula as seen by the Hubble Space Telescope. Image courtesy NASA, ESA, M. Robberto (Space Telescope Science Institute/ESA) and the Hubble Space Telescope Orion Treasury Project Team.
Indeed, how is it possible that all the phenomena observed in classical electricity and magnetism can be explained by means of just four mathematical equations? Furthermore, physicist James Clerk Maxwell (after whom those four equations of electromagnetism are named) showed in 1864 that the equations predicted that varying electric or magnetic fields should generate propagating waves. These waves—the familiar electromagnetic waves—were eventually detected by the German physicist Heinrich Hertz in a series of experiments conducted in the late 1880s. And if that is not enough, the modern theory of electrodynamics, known as quantum electrodynamics (QED), is even more astonishing. In 2006 a group of physicists at Harvard University determined the magnetic moment of the electron (which measures how strongly the electron interacts with a magnetic field) to a precision of eight parts in a trillion. Calculations of the electron's magnetic moment based on QED reach the same precision and the two results agree! What is it that gives mathematics such incredible powers? In the present short article I will not even attempt to answer this intricate question. I will rather present some less familiar aspects of the problem itself.
The puzzle of the power of mathematics is in fact even more complex than the above example of electromagnetism might suggest. There are actually two facets to the "unreasonable effectiveness," one that I will call active and another that I dub passive. The active facet refers to the fact that when scientists attempt to light their way through the labyrinth of natural phenomena, they use mathematics as their torch. In other words, at least some of the laws of nature are formulated in directly applicable mathematical terms. The mathematical entities, relations, and equations used in those laws were developed for a specific application. Newton, for instance, formulated the branch of mathematics known as calculus because he needed this tool for his equations of motion. Similarly, string theorists today often develop the mathematical machinery they need. The passive effectiveness, on the other hand, refers to cases in which abstract mathematical theories had been developed with absolutely no applications in mind, only to turn out decades, or sometimes centuries later, to be powerfully predictive physical models. In what follows I will describe a wonderful example of the continuous interplay between active and passive effectiveness.
To be or knot to be
In the Greek legend of the Gordian knot Alexander the Great used his sword to slice through a knot that had defied all previous attempts to untie it. Knots, and especially maritime knots, enjoy a long history of legends and fanciful names such as "Englishman's tie," "hangman's knot," and "cat's paw". Knots became the subject of serious scientific investigation when in the 1860s the English physicist William Thomson (better known today as Lord Kelvin) proposed that atoms were in fact knotted tubes of ether (that mysterious substance that was supposed to permeate space). In order to be able to develop something like a periodic table of the elements, Thomson had to be able to classify knots—find out which different knots are possible. This particular need sparked a great interest in the mathematical theory of knots. This is a perfect example of what I dubbed the active aspect of the effectiveness of mathematics. In other words, physicists and mathematicians thought that knots were viable models for atoms, and consequently they enthusiastically engaged in the mathematical study of knots.
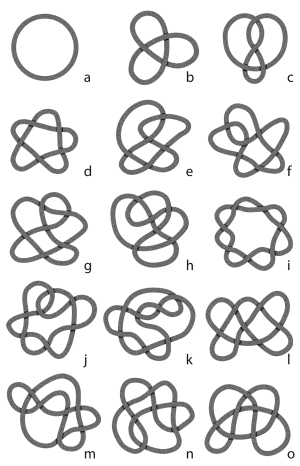
Figure 1: A selection of knots. Image created by Ann Feild.
A mathematical knot looks very much like a familiar knot in a string, only with the string's ends spliced (a few examples of knots are shown in figure 1). In Thomson's theory, knots such as the ones in figure 1a (the unknot), figure 1b (the trefoil knot) and figure 1c (the figure eight knot) could, in principle at least, model atoms of increasing complexity, such as the hydrogen, carbon, and oxygen atoms, respectively. For knots to be truly useful, however, mathematicians searched for some precise way of proving that what appeared to be different knots (such as the trefoil knot and the figure eight knot) were really different—they couldn't be transformed one into the other by some simple manipulation. Towards the end of the nineteenth century, the Scottish mathematician Peter Guthrie Tait and the University of Nebraska professor Charles Newton Little published complete tables of knots with up to ten crossings. Unfortunately, by the time that this heroic effort was completed, Kelvin's theory had already been totally discarded as a model for atomic structure. Still, even without any other application in sight, the mathematical interest in knot theory continued at that point for its own sake. The only difference was that, as the British mathematician Sir Michael Atiyah has put it, "the study of knots became an esoteric branch of pure mathematics."
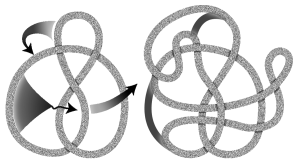
Figure 2: Deforming a knot. Image created by Ann Feild.
One of the main goals of knot theory has always been to identify properties that truly distinguish knots—to find what are known as knot invariants. A knot invariant acts very much like a "fingerprint" of the knot; it does not change by superficial deformations of the knot (for example, of the type demonstrated in figure 2). At first blush, you may think that the minimum number of crossings in a knot could serve as such an invariant. After all, no matter how hard you try, you will never be able to reduce the number of crossings of the trefoil knot (figure 1b) to fewer than three. However, the minimum number of crossings is actually not a very useful invariant. As figure 1 demonstrates, there are three different knots with six crossings and no fewer than seven different knots with seven crossings.
Two major breakthroughs in knot theory occurred in 1928 and in 1984. In 1928, the American mathematician James Waddell Alexander discovered an algebraic expression (known as the Alexander polynomial) that uses the arrangement of crossings to label the knot. For example, the Alexander polynomial for the trefoil knot is t2−t+1. Two knots that have different Alexander polynomials are indeed different (e.g., the Alexander polynomial for the figure eight knot is t2−3t+1). Unfortunately, two knots that have the same Alexander polynomial may still be different. Consequently, while it was certainly very useful, the Alexander polynomial was still not perfect for classifying knots. Decades of work in the theory of knots finally produced the second breakthrough in 1984. The New Zealander-American mathematician Vaughan Jones detected an unexpected relation between knots and another abstract branch of mathematics (known as von Neumann algebras). This led to the discovery of a more sensitive invariant than the Alexander polynomial, which became known as the Jones polynomial. The Jones polynomial distinguishes, for instance, even between knots and their mirror images (figure 3), for which the Alexander polynomials were identical.
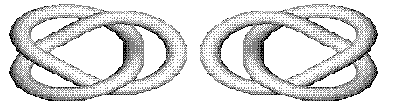
Figure 3: A knot and its mirror image. Image created by Ann Feild.
In particular, string theorists Hirosi Ooguri and Cumrun Vafa discovered that the number of complex topological structures that are formed when many strings interact is related to the Jones polynomial. Furthermore, the leading string theorist Ed Witten demonstrated that the Jones polynomial affords new insights in one of the most fundamental areas of research in modern physics, known as quantum field theory.

Knots leading the way, from the atom to pure maths and back to physical matter.
The lesson from this very brief history of knot theory is remarkable. First, it was the active effectiveness of mathematics that came into play. Physicists needed a model for the atom, and when knots appeared to provide the appropriate tool, a mathematical theory of knots took off. When a better mathematical model (in the form of the Bohr atom) was discovered, mathematicians did not abandon knot theory. Driven only by their curiosity, they continued to explore the properties of knots for many decades. The mere possibility of understanding the properties of knots and the principles that govern their classification was seen by most mathematicians as exquisitely beautiful and essentially irresistible. However, then came the surprising passive effectiveness of mathematics. Unexpectedly, the Jones polynomial and knot theory in general turned out to have wide-ranging applications in string theory.
What makes this story even more striking is the following fact. Recall that Thomson started to study knots because he was searching for a theory of atoms, then considered to be the most basic constituents of matter. By a remarkably circular twist of history, knots are now found to provide answers in string theory, our present-day best effort to understand the constituents of matter! So knot theory emerged from an attempt to explain physical reality, then it wandered into the abstract realm of pure mathematics—only to eventually return to its ancestral origin. Isn't this absolutely amazing?
About the author

Mario Livio's book Is God a Mathematician? is scheduled to appear on January 6, 2009 and reviewed in this issue of Plus. It follows the lives and thoughts of some of the greatest mathematicians in history, and attempts to explain the "unreasonable effectiveness" of mathematics.
Dr Mario Livio is a senior astrophysicist at the Space Telescope Science Institute (STScI), the institute which conducts the scientific program of the Hubble Space Telescope. He received his PhD in theoretical astrophysics from Tel Aviv University in Israel, was a professor in the Physics Dept. of the Technion-Israel Institute of Technology from 1981 till 1991, and joined STScI in 1991. Dr Livio has published over 400 scientific papers and received numerous awards for research and for excellence in teaching. His book, The Golden Ratio, won him the Peano Prize and the International Pythagoras Prize in 2004.His interests span a broad range of topics in astrophysics, from cosmology to the emergence of intelligent life. Dr Livio has done much fundamental work on the topic of accretion of mass onto black holes, neutron stars, and white dwarfs, as well as on the formation of black holes and the possibility to extract energy from them. During the past decade, Dr Livio's research focused on supernova explosions and their use in cosmology to determine the nature of the dark energy that pushes the universe to accelerate, and on extrasolar planets.